1.7: Tema Avanzado - Derivación de la Relación Tensión-Desplazamiento para Placas Delgadas

La hipótesis de Love-Kirchoff extiende los supuestos unidimensionales de Euler-Bernoulli en placas. Una placa se puede doblar en dos direcciones, formando una superficie de doble curvatura. Por lo tanto, ahora se requieren las propiedades plano-permanece-plano y normal-permanece-normal en ambas direcciones. Así, la Ecuación (1.5.1) y la Ecuación (1.5.2) toman la forma

\[u_{\alpha} = u_{\alpha}^{\circ} - \theta_{\alpha} z\]

\[\theta_{\alpha} = \frac{\partial w}{\partial x_{\alpha}} \buildrel \rm {def} \over{=} w_{,\alpha}\]

donde\(\theta_{\alpha}\) está la pendiente (rotación) en\(x_{\alpha}\) -dirección. Al eliminar\(\theta_{\alpha}\) entre la ecuación anterior, se obtiene la familiar dependencia lineal de los componentes en el plano del vector de desplazamiento en la coordenada z

\[u_{\alpha}(x_{\alpha}, z) = u_{\alpha}^{\circ}(x_{\alpha}) − zw_{,\alpha} \label{1.7.3}\]

El espesor constante\((w = \dot{w}(x_{\alpha}))\) es el tercer supuesto cinemático de la teoría de placas.

Ahora, observe cuidadosamente cómo se calculan los componentes de deformación en la placa. Teniendo en cuenta todos los componentes del tensor de deformación, se pueden distinguir tres componentes de deformación en el plano\(\epsilon_{\alpha \beta}\) (área enmarcada en la matriz de abajo) y tres componentes fuera del plano.

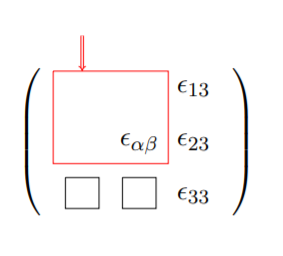
El componente de deformación de espesor pasante se desvanece asumiendo la independencia del desplazamiento vertical en la coordenada\(z\)

\[\epsilon_{33} = \epsilon_{zz} = \frac{\delta w}{\delta z} = 0\]

Los dos componentes de cizallamiento fuera del plano del tensor de deformación\(\epsilon_{\alpha 3}\) desaparecen debido a la hipótesis LoveKirchoff, Ecuación\ ref {1.7.3},

\[\epsilon_{\alpha 3} = \frac{1}{2} \left( \frac{\delta u_{\alpha}}{\delta z} + \frac{\delta w}{\delta x_{\alpha}} \right) = \frac{1}{2} (u_{\alpha , z} + w_{, \alpha}) = \frac{1}{2} \left[ \frac{d}{d z} (u_{\alpha}^{\circ}(x_{\alpha}) + w_{,\alpha} \right] = 0\]

Los componentes que no se desvanecen del tensor de deformación son los componentes de deformación en el plano

\[\epsilon_{\alpha \beta} = \frac{1}{2} (u_{\alpha , \beta} + u_{\beta , \alpha}) \alpha, \beta = 1, 2\]

donde\(u_{\alpha}\) se define por la Ecuación (1.3.9). Realización de la diferenciación que uno obtiene

\[\epsilon_{\alpha \beta} = \frac{1}{2} [ u_{\alpha}^{\circ} - zw_{, \alpha}]_{, \beta} + \frac{1}{2} [ u_{\beta}^{\circ} − zw_{,\beta}]_{, \alpha} = \frac{1}{2} (u_{\alpha , \beta}^{\circ} + u_{\beta , \alpha}^{\circ}) - \frac{1}{2} z [ w_{,\alpha \beta} + w_{,\beta \alpha}] \label{1.7.7}\]

El primer término en la Ecuación\ ref {1.7.7} es la tensión\(\epsilon_{\alpha \beta}^{\circ}\) derivada de la acción de la membrana en la placa. Es un gradiente simétrico del desplazamiento del plano medio\(u_{\alpha}^{\circ}\). Dado que el orden de diferenciación parcial no es importante, la Ecuación\ ref {1.7.7} simplifica a

\[\epsilon_{\alpha \beta}(x_{\alpha}, z) = \epsilon_{\alpha \beta}^{\circ}(x_{\alpha}) − zw_{,\alpha \beta}\]

Definir el tensor de curvatura\(\kappa_{\alpha \beta}\) mediante

\[\kappa_{\alpha \beta} = −w_{,\alpha \beta} = − \frac{\partial^2 w}{\partial x_{\alpha} \partial x_{\beta}}\]

La relación deformación-desplazamiento para placas delgadas toma la forma final

\[\epsilon_{\alpha \beta} = \epsilon_{\alpha \beta}^{\circ} + z\kappa_{\alpha \beta}\]

donde

\[\epsilon_{\alpha \beta}^{\circ} = \frac{1}{2}(u_{\alpha , \beta}^{\circ} + u_{\beta , \alpha}^{\circ})\]