1.8: Forma expandida de relación deformación-desplazamiento

Habiendo derivado las relaciones geométricas en las notaciones tensoriales, las ecuaciones (1.7.10) y (1.7.11) serán reescritas en el sistema de coordenadas (x, y) y se dará interpretación física a cada término. Considerar primero (1.7.11)

\[\alpha = 1, \beta = 1 \; x_1 = x, \; \epsilon_{xx}^{\circ} = \frac{1}{2} \left( \frac{\partial u_{x}^{\circ}}{\partial x} + \frac{\partial u_{x}^{\circ}}{\partial x} \right) = \frac{\partial u_{x}^{\circ}}{\partial x} \]

\[\alpha = 2, \beta = 2 \; x_2 = y, \; \epsilon_{xx}^{\circ} = \frac{1}{2} \left( \frac{\partial u_{y}^{\circ}}{\partial y} + \frac{\partial u_{y}^{\circ}}{\partial y} \right) = \frac{\partial u_{y}^{\circ}}{\partial y} \]

\[\alpha = 1, \beta = 2 \; x_1 = x, x_2 = y, \; \epsilon_{xy}^{\circ} = \frac{1}{2} \left( \frac{\partial u_{x}^{\circ}}{\partial y} + \frac{\partial u_{y}^{\circ}}{\partial x} \right) \]

\(\epsilon_{yy}^{\circ}\)Los componentes\(\epsilon_{xx}^{\circ}\) y denotan tensiones de la superficie media de la placa en las\(y\) direcciones\(x\) y, respetuosamente. Las deformaciones de membrana se deben a los desplazamientos impuestos o fuerzas de membrana aplicadas a los bordes. En la teoría de la pequeña desviación de las placas, la carga de presión lateral no producirá deformaciones de membrana. Por el contrario, las tensiones de membrana sí se desarrollan en la teoría de la desviación moderadamente grande de las placas debido a la carga transversal. Este tema será tratado más adelante en el Capítulo 6.

El tercer componente del tensor de deformación es la deformación por cizallamiento en el plano\(\epsilon_{xy}^{\circ}\). Representa el cambio de ángulos en el plano de la placa debido a la carga de cizallamiento en los bordes. La interpretación geométrica del tensor de deformación de membrana es similar a la dada para el tensor de deformación general en las Figuras (1.2.2) y (1.2.3).

El tensor de curvatura\(\kappa_{\alpha \beta}\) requiere una explicación cuidadosa. Considerar un segmento infinitesimal ds de una curva y encajar en él un círculo de un radio instantáneo ρ, Figura (\(\PageIndex{1}\)). Entonces

\[ds = \rho d\theta \]

Figura\(\PageIndex{1}\): Cambio de pendiente de una línea entre dos puntos

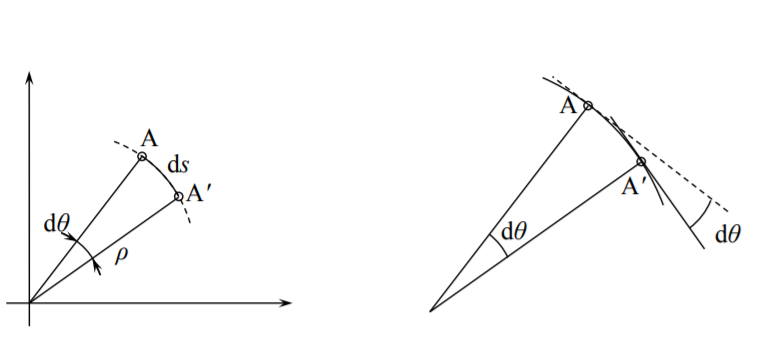
Matemáticamente, la curvatura de cualquier línea\(\kappa\) es el cambio de la pendiente a medida que uno se mueve a lo largo de la curva

\[\kappa \buildrel \rm {def} \over{=} \frac{d\theta }{ds} \label{1.8.5}\]

Al comparar la Ecuación\ ref {1.8.5} con la Ecuación (1.7.2), la curvatura en\([ \frac{1}{m} ]\) es la reciprocidad del radio de curvatura\(\kappa = \frac{1}{\rho}\). El primer componente del tensor de curvatura, definido por la Ecuación (1.7.10) es

\[\alpha = 1, \beta = 1 \; x_1 = x \; \kappa_{xx} = -\frac{\partial^2 w}{\partial x^2} = -\frac{\partial}{\partial x} \left( \frac{\partial w}{\partial x} \right) = \frac{\partial}{\partial x} ( - \theta_{x})\]

Este será el único componente del tensor de curvatura si la placa está sujeta a la llamada flexión cilíndrica.

Figura\(\PageIndex{2}\): (a) flexión cilíndrica de una placa, y (b) flexión con torsión.

La interpretación de los\(\kappa_{yy}\) componentes del tensor de curvatura

\[\alpha = 2, \beta = 2 \; x_2 = y \; \kappa_{yy} = -\frac{\partial^2 w}{\partial y^2} = -\frac{\partial}{\partial y} ( - \theta_{y})\]

es similar como antes. Más interesante es el componente mixto del tensor de curvatura

\[\alpha = 1, \beta = 2 \; x_1 = x, x_2 = y \; \kappa_{xy} = -\frac{\partial^2 w}{\partial x \partial y} = -\frac{\partial}{\partial y} ( - \theta_{x})\]

Para detectar\(\kappa_{xy}\) se tiene que verificar si la pendiente en una dirección, digamos\(\theta_x\) cambia a lo largo\(y\) de la segunda dirección. No lo hace para una flexión cilíndrica, Figura (1.4.2 (a)). Pero si lo hace, la placa se tuerce, como se muestra en la Figura (1.4.2 (b)). Por lo tanto, el componente\(\kappa_{xy}\) se llama giro.

Un parámetro importante que distingue entre estas clases de la forma deformada de una placa es la curvatura gaussiana,\(\kappa_{G}\). La curvatura gaussiana se define como un producto de dos curvaturas principales

\[\kappa_{G} = \kappa_I\kappa_{II}\]

La curvatura es un tensor, por lo que sus componentes cambian girando el sistema de coordenadas un ángulo\(\psi\) a una nueva dirección (x\ prime, y\ prime). Existe uno de esos ángulos\(\psi_p\) para el que desaparecen los componentes de torsión. Los componentes diagonales restantes se denominan curvatura principal. La cobertura completa de las fórmulas de transformación para vectores y tensores se presenta en la recitación 2. Usando estos resultados, la curvatura gaussiana se puede expresar en términos de los componentes del tensor de curvatura

\[\kappa_{G} = \kappa_{xx} \kappa_{yy} − \kappa_{xy}^2\]

Para la flexión cilíndrica el giro κxy así como una de las principales curvaturas se desvanecen de manera que la curvatura gaussiana es cero. El signo de la curvatura gaussiana distingue entre tres tipos de la placa deformada, el cuenco, el cilindro y el sillín, Figura (\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Placa deformada con tres clases diferentes de formas.

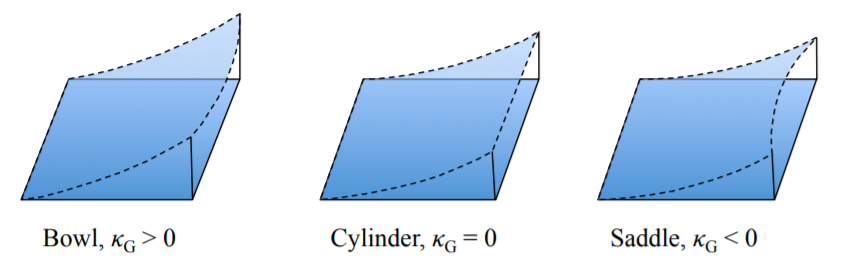
La consideración de la curvatura gaussiana introduce importantes simplificaciones en la formulación y aplicaciones del método energético en la mecánica estructural. Se dedicará una conferencia separada a este tema.