1.9: Defecciones moderadamente grandes de vigas y placas

En el curso 2.081 Placas y Conchas se presenta una presentación completa de la teoría de las deflexiones moderadamente grandes de las placas, derivada de los primeros principios. Las notas de clase para este curso están disponibles en OpenCourseWare. Allí se deriva la relación deformación-desplazamiento para la teoría de la desviación moderadamente grande de las vigas. Aquí las ecuaciones correspondientes para las planchas solo se establecen con una interpretación física. Un lector interesado es referido a las notas de Placas y Conchas para más detalles.

Definición de deflexiones moderadamente grandes de vigas

Cuáles son las “deflexiones moderadamente grandes” y en qué se diferencian de la “pequeña desviación”. Para ver la diferencia, es necesario considerar la configuración inicial y deformada del eje de la viga. El elemento de longitud inicial y actual en la configuración no deformada y deformada respectivamente se denota dx y ds, como en la Figura (\(\PageIndex{1}\))

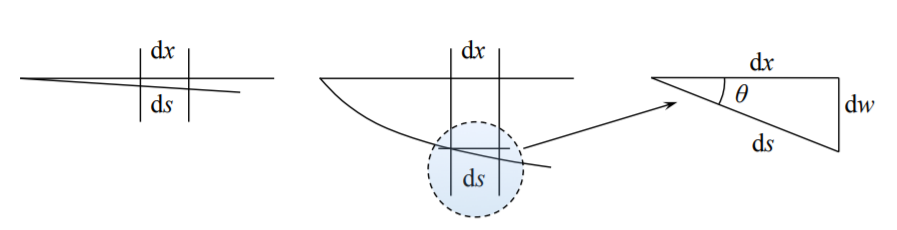
Figura\(\PageIndex{1}\): Cambio de longitud del eje de viga producido por rotación.

De la geometría del problema

\[dx = ds \cos \theta \approx ds \left[1 − \frac{\theta^2}{2}\right] \label{1.9.1}\]

Se puede distinguir entre tres teorías:

(i) Pequeñas deflexiones, geometría lineal\(\theta^2 \ll 1, \; dx \approx ds\), Figura (\(\PageIndex{1}\)(a)).

ii) Deflexiones moderadamente grandes. La expansión de dos términos de la función coseno da una buena aproximación para\(0 < \theta < 10^{\circ}\). La relación entre d\(x\) y d\(s\) viene dada por la Ecuación\ ref {1.9.1}, Figura\(\PageIndex{1}\) ((b)).

(iii) Para mayor rotación, se debe considerar una total no linealidad del problema.

La presente derivación se refiere al caso (ii) anterior. Se adopta la medida de deformación de Cauchy, definida en la Ecuación (1.1.3):

\[\epsilon = \frac{ds^2-dx^2}{2dx^2}\]

La longitud actual d se\(s\) puede expresar en términos de d\(x\) y d\(w\), ver Figura (\(\PageIndex{1}\))

\[ds^2 = dx^2 + dw^2\]

De las dos ecuaciones anteriores, la deformación del eje de la viga debido a la rotación del elemento,\(\epsilon_{\text{rot}}\) es

\[\epsilon = \frac{1}{2} \left( \frac{dw}{dx} \right)^2 = \frac{1}{2}\theta^2\]

El eje del haz también se extiende debido al gradiente de la componente axial del vector de desplazamiento, definido por la Ecuación (1.5.13). Por lo tanto, la deformación total del eje de la viga debido a la extensión y rotación combinadas es

\[\epsilon^{\circ} = \frac{du}{dx} + \frac{1}{2} \left( \frac{dw}{dx} \right)^2 \]

Se puede notar que el segundo término en la ecuación anterior es siempre positivo mientras que el primer término puede ser positivo o negativo. En un caso especial los dos términos pueden cancelarse entre sí aunque una viga sufra una gran deformación.

La pregunta que a menudo hacen los estudiantes es si la expresión para la curvatura, dada por la Ecuación (1.5.14) también debe modificarse debido a una mayor rotación. Desde el punto de vista matemático la respuesta es SÍ. Pero los ingenieros tienen una manera de sortearlo.

En el sistema de coordenadas rectangulares la definición exacta de la curvatura de la línea es:

\[\kappa = \frac{-\frac{d^2w}{dx^2}}{\left( 1+ \left(\frac{dw}{dx}\right)^2\right)^{3/2}} \label{1.9.6}\]

En el límite se recupera\(\frac{dw}{dx} \rightarrow 0\) la definición lineal de la ecuación no lineal Ecuación\ ref {1.9.6}. La diferencia entre la Ecuación (1.5.14) y la Ecuación\ ref {1.9.6} es pequeña en el caso de una desviación moderadamente grande.

La deformación total en un punto arbitrario de un haz sometido a deflexión moderadamente grande es

\[\epsilon = \underbrace{\frac{du}{dx} + \frac{1}{2} \left( \frac{dw}{dx} \right)^2}_{\text{membrane strain} \; \epsilon^{\circ}} + \underbrace{z\kappa}_{\text{bending strain} \; z\kappa}\]

Extensión a la deflexión moderadamente grande de las placas

En la notación tensorial compacta, la relación deformación-desplazamiento no lineal toma la forma

\[\epsilon_{\alpha \beta} = \frac{1}{2}(u_{\alpha , \beta} + u_{\beta , \alpha}) + \frac{1}{2} w_{, \alpha} w_{ , \beta} + z\kappa_{\alpha \beta}\]

Al comparar con una expresión similar para la teoría de deflexión pequeña, Ecuación (1.7.10) y Ecuación (1.7.11), el nuevo término no lineal es

\[\frac{1}{2} w_{, \alpha} w_{ , \beta} = \frac{1}{2} \frac{\partial w}{\partial x_{\alpha}} \frac{\partial w}{\partial x_{\beta}}\]

Este término forma una\(2 \times 2\) matriz:

\ [\ izquierda|\ begin {array} {cc}
\ frac {1} {2}\ izquierda (\ frac {\ w parcial} {\ parcial x}\ derecha) ^ {2} &\ frac {1} {2}\ frac {\ w parcial} {\ w parcial}\ frac {\ parcial x} {\ parcial y}\
\ frac {1} {2} frac {\ w parcial} {\ parcial y}\ frac {\ w parcial} {\ parcial x} &\ frac {1} {2}\ izquierda (\ frac {\ parcial w} {\ parcial y}\ derecha) ^ {2}
\ end {array}\ derecha|=\ izquierda|\ begin {array} {c}
\ frac {\ theta_ {x} ^ {2}} {2},\ frac {1} {2}\ theta_ {x}\ theta_ {y}\
\ frac {1} {2}\ theta_ {x}\ theta_ {y},\ frac {\ theta_ {y} ^ {2}} {2}
\ fin {array}\ derecha|\]

Los términos diagonales representan el cuadrado de la pendiente de la forma de deflexión en\(x\) y\(y\) direcciones. Los términos no diagonales son simétricos y son producto de pendientes en las dos direcciones. Este término se desvanece para la flexión cilíndrica.