10.2: pandeo de una placa simplemente soportada
- Page ID
- 85263
La forma expandida de la ecuación gobernante correspondiente al tipo de carga asumido es
\[D \left[ \frac{\partial^4 w}{\partial x^4} + 2 \frac{\partial^4 w}{\partial x^2\partial y^2} + \frac{\partial^4}{\partial y^4}\right]+ \bar{N}\frac{d^2 w}{dx^2} = 0\]
La solución de la ecuación diferencial parcial lineal anterior con coeficiente constante se busca como producto de dos funciones armónicas
\[w(x, y) = \sin \frac{m \pi x}{a} \sin \frac{n \pi y}{b}\]
donde\(m\) y\(n\) son número de medias ondas en las direcciones longitudinal y transversal, respectivamente. La función\(w(x, y)\) satisface la condición de límite para el desplazamiento. El momento de flexión\(M_n\)
\[M_n = M_{xx} = D [\kappa_{xx} + \nu\kappa_{yy}] = −D \left[ \left(\frac{m \pi}{a}\right)^2 + \nu \left(\frac{n \pi}{b}\right)^2 \right] \sin \frac{m \pi x}{a} \sin \frac{n \pi y}{b} \label{11.12}\]
se desvanece en\(x = 0\) y\(x = a\) bordes. También en\(y = 0\) y\(y = b\),\(M_n = M_{yy}\) es cero. Por lo tanto, la función propuesta satisface la condición de límite simplemente soportada en los cuatro bordes. Sustituyendo la función\(w(x, y)\) en la ecuación gobernante, se obtiene
\[\left\{ D \left[ \left(\frac{m \pi}{a}\right)^4 + 2\left(\frac{m \pi}{a}\right)^2 \left(\frac{n \pi}{b}\right)^2 + \left(\frac{n \pi}{b}\right)^4 \right] - \bar{N} \left(\frac{m\pi}{a}\right)^2 \right\} \sin \frac{m \pi x}{a} \sin \frac{n \pi y}{b} = 0 \]
La ecuación diferencial se satisface para todos los valores de\((x, y)\) si los coeficientes satisfacen
\[\bar{N} = D \left(\frac{\pi a}{m}\right)^2 \left[ \left(\frac{m}{a}\right)^2 + \left(\frac{n}{b}\right)^2 \right]^2 \]
Se ve que el valor más pequeño de\(\bar{N}\) para todos los valores de\(a\),\(b\) y\(m\) se obtiene si\(n = 1\). Esto significa que solo se formará una media onda en la dirección perpendicular a la aplicación de carga. Entonces, la Ecuación\ ref {11.12} se puede poner en una forma simple
\[\bar{N}_c = k_c \frac{\pi^2 D}{b^2} \]
donde el coeficiente de pandeo\(k_c\) es una función tanto de la relación\(a/b\) de aspecto de la placa como del parámetro de longitud de onda
\[k_c = \left( \frac{mb}{a} + \frac{a}{mb} \right)^2 \]
El parámetro\(m\) es un número entero y determina cuántas medias ondas encajarán en la longitud de la placa. Se conoce la relación de aspecto, pero aún\(a/b\) se desconoce el parámetro de longitud de onda. Su valor debe ser encontrado por inspección, es decir, trazando el coeficiente de pandeo en función de\(a/b\) para los valores posteriores del parámetro\(m\). Esto se muestra en la Figura (\(\PageIndex{1}\)).
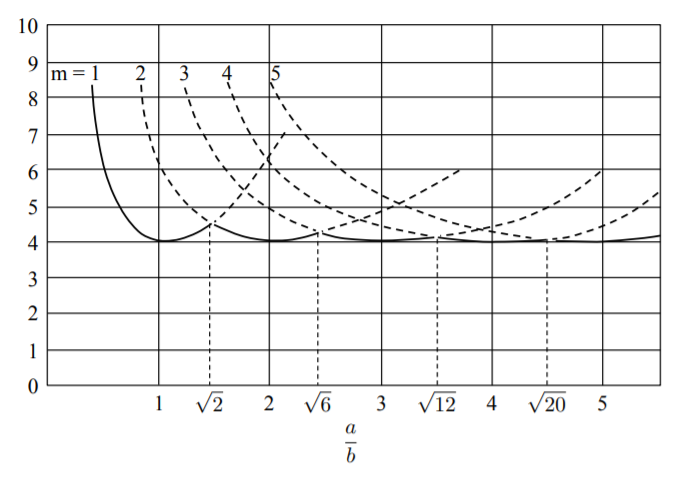
Por ejemplo, el coeficiente de pandeo correspondiente a los cinco primeros modos de pandeo correspondientes a\(\frac{a}{b} = 2\) son
| \(m\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(k_c\) | 6.2 | 4 | 4.7 | 6.2 | 8.4 |
La carga de pandeo más baja\(k_c = 4\) se produce cuando hay dos medias ondas a lo largo de la longitud de la placa,\(m = 2\). La línea que separa el área segura y sombreada en la Figura (\(\PageIndex{2}\)) y la insegura mientras que el área define únicamente el coeficiente de pandeo para todas las combinaciones de\(a/b\) y\(m\).
Consideremos ahora una placa larga,\(a \gg b\) para la cual el parámetro\(m\) puede ser tratado como una variable continua. En este caso hay un mínimo analítico del coeficiente de pandeo
\[ \frac{dk_c}{dm} = 0 \quad \rightarrow \quad a = mb \]
El resultado anterior significa que la placa se divide en un número entero de cuadrados con hoyuelos convexos y cóncavos alternados.
Qué sucede cuando la placa rectangular mostrada en la Figura (10.1.1) está restringida a la expansión lateral
\[u_y(y = 0) = u_y(y = b) = 0 \]
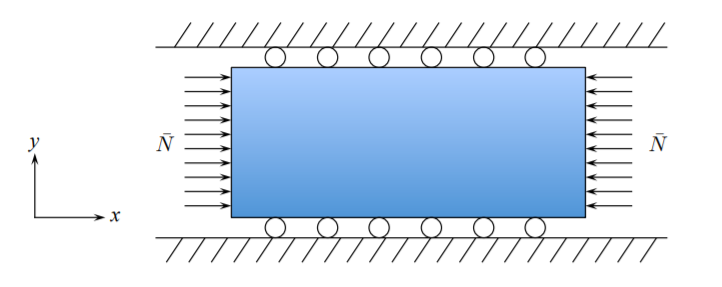
Sin deformación en la dirección y\(\epsilon_{yy} = 0\), las ecuaciones constitutivas (11.6) se reducen a
\[N_{xx} = C\epsilon_{xx}^{\circ}\]
\[N_{yy} = C\nu \epsilon_{xx}^{\circ}\]
Esto significa que\(N_{yy} = \nu N_{xx}\) se desarrolla una fuerza de reacción en la dirección transversal. La forma abrochada de la placa es la misma y la solución, Ecuación (?? ) aún se mantiene pero la nueva expresión para el coeficiente de pandeo es
\[k_c = \frac{\left[ \left(\frac{mb}{a}\right)^2 + n^2 \right]^2}{\left(\frac{mb}{a}\right)^2 + \nu n^2}\]
El menor valor del coeficiente de pandeo se puede encontrar por inspección. Tomando de nuevo como ejemplo\(a/b = 2\), los valores del coeficiente de pandeo correspondientes a los nueve primeros modos de pandeo son
| \(n\)\\(m\) | 1 | 2 | 3 |
|---|---|---|---|
| \ (n\)\\(m\) "alcance="fila">1 | 10/7 | 3 | 4.09 |
| \ (n\)\\(m\) "alcance="fila">2 | 3.8 | 10.7 | 10.9 |
| \ (n\)\\(m\) "alcance="fila">3 | 26 | 25 | 24.1 |
El valor más bajo del coeficiente de pandeo\(k_c = 3\) corresponde a dos medias ondas en la dirección de carga y una media onda en dirección transversal. Se ve que restringir la deformación en el plano no cambia el modo de pandeo sino que reduce la carga de pandeo en un factor de\(3/4\). La fuerza de compresión de reacción hace que la placa se doble más fácilmente. En este ejemplo se subraya la importancia de definir adecuadamente las condiciones de contorno no solo en la dirección fuera del plano sino también en las direcciones dentro del plano.


