10.5: Respuesta de Placas Post-pandeo (Avanzada)
- Page ID
- 85268
Supongamos que la placa está sujeta a una compresión axial monótonamente creciente\(u_o\), Figura (\(\PageIndex{1}\)).
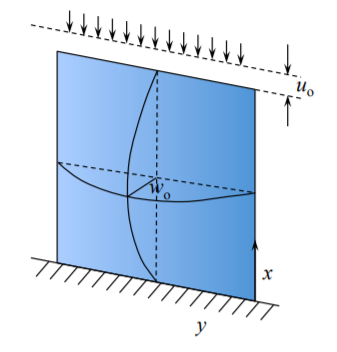
Inicialmente la placa es recta y en el estado de prepandeo hay compresión uniaxial y deformación biaxial. Esta etapa se analizó en la Sección 6.1. No hubo desplazamiento fuera del plano\(w_o\). El punto de bifurcación se probó imponiendo un pequeño campo arbitrario de desplazamiento fuera del plano. Ahora, parte de la energía de compresión se alivia, pero la energía de flexión aparece para que la energía potencial total del sistema siga siendo la misma.
El valor correspondiente de la carga (carga de pandeo) bajo la cual esto sucede se derivó en la Sección 6.2. Lo que sucede con la placa después de que se haya producido el pandeo es el tema de la presente sección. Se supone que la deformación de la placa es una superposición de la compresión en el plano. La forma del desplazamiento en plano es similar a la de la solución de prepandeo, Ecuación (?? ), pero ahora debería agregarse un término más a la expresión for para\(u_y\) satisfacer la tracción cero en los bordes descargados.
\[u_x = u_o \left( 1 − \frac{x}{a}\right)\]
\[u_y = \nu u_o \frac{y}{a} + f(x) \]
El campo de deformación fuera del plano se toma idéntico al de la solución de pandeo
\[w = w_o \sin \frac{\pi x}{a} \sin \frac{\pi y}{b}\]
que satisface las condiciones de contorno simplemente soportadas en los cuatro bordes. Aquí se supone que la placa es infinitamente larga o es cuadrada de manera que eso\(a = b\).
La energía potencial total del sistema es
\[\prod = U_b + U_m − P U_o \]
donde\(P = bN\) y la expresión para las energías de flexión y membrana están dadas por las Ecuaciones (3.6.25) y (3.6.41), respectivamente. El tensor de curvatura se define por
\[\kappa_{\alpha\beta} = −w_{,\alpha\beta} \]
y para la forma asumida\(w(x, y)\) tiene tres componentes
\[\kappa_{\alpha\beta} = w_o \left(\frac{\pi}{a}\right)^2 \begin{vmatrix} \sin \frac{\pi x}{a} \sin \frac{\pi y}{a} & - \cos \frac{\pi x}{a} \cos \frac{\pi y}{a} \\ - \cos \frac{\pi x}{a} \sin \frac{\pi y} {a} & \sin \frac{\pi x}{a} \sin \frac{\pi y}{a} \end{vmatrix}\]
La deformación de membrana es el resultado del gradiente del vector de desplazamiento en el plano y la rotación moderadamente grande de los elementos de placa
\[\epsilon_{\alpha\beta} = \frac{1}{2} (u_{\alpha,\beta} + u_{\beta,\alpha}) + \frac{1}{2} w_{,\alpha} w_{,\beta} \]
Los componentes de los tensores extensibles en el plano son
\[\left.\begin{array}{l} \epsilon_{xx} = − \frac{u_o}{a} + \frac{w^2_o}{2} \left(\frac{\pi}{a}\right)^2 \cos^2 \frac{\pi x}{a} \sin^2 \frac{\pi y}{a} \\ \epsilon_{yy} = \nu\frac{u_o}{a} + f^{\prime}(x) + \frac{w^2_o}{2} \left(\frac{\pi}{a}\right)^2 \sin^2 \frac{\pi x}{a} \cos^2 \frac{\pi y}{a} \end{array}\right\} \]
\[\epsilon_{xy} = \frac{w^2_o}{2} \left( \frac{\pi}{a}\right)^2 \cos^2 \frac{\pi x}{a} \cos^2 \frac{\pi y}{a} \]
Se ve que la forma de la tensión axial\(\epsilon_{xx}\) proporciona acoplamiento entre la amplitud en el plano\(u_o\) y la amplitud fuera del plano\(w_o\).
La expresión general para la energía de flexión de la placa, Ecuación (3.6.25) es
\[U_b = \frac{D}{2} \int^{a}_{0} \int^{a}_{0} \{(\kappa_{xx} + \kappa_{yy})^2 − 2(1 − \nu)\kappa_G\} dx dy \]
donde\(\kappa_G = \kappa_{xx}\kappa_{yy} − \kappa^2_{xy}\) está la curvatura gaussiana. Se puede demostrar fácilmente que la curvatura gaussiana integrada sobre la superficie de la placa es cero. Por lo tanto, el segundo término en el integrando de la Ecuación (10.3.1) desaparece. Finalmente, se calcula que la energía total de flexión de la placa es
\[U_b = \frac{1}{2} Dw^2_o \frac{\pi^4}{a^2} \]
Antes de proceder a calcular la energía de deformación de membrana, la función desconocida\(f(x)\) en la Ecuación (?? ) debe determinarse a partir de la condición límite\(N_{yy}(y = a \text{ and } y = 0) = 0\). La ley de elasticidad al estrés plano es
\[N_{xx} = C(\epsilon_{xx} + \nu \epsilon_{yy}) \]
\[N_{yy} = C(\epsilon_{yy} + \nu \epsilon_{xx}) \]
\[N_{xy} = (1 - \nu) C \epsilon_{xy} \]
De la Ecuación (10.2.10-10.2.11), la fuerza de membrana en el plano en la dirección y es
\[N_{yy} =C \left[ \nu \frac{u_o}{a} + \frac{1}{2} w^2_o \left(\frac{\pi}{a}\right)^2 \sin^2 \frac{\pi x}{a} \cos^2 \frac{\pi y}{a} + f^{\prime} \\ −\nu \frac{u_o}{a} + \frac{\nu}{2} w^2_o \left(\frac{\pi}{a}\right)^2 \cos^2 \frac{\pi x}{a} \sin^2 \frac{\pi y}{a} \right] \]
La fuerza de la membrana cambia de punto a punto y en los bordes descargados\(y = 0\) y\(y = a\) es
\[N_{yy} (0, a) = C \left[ \frac{1}{2} w^2_o \left(\frac{\pi}{a}\right)^2 \ sin^2 \frac{\pi x}{a} + f^{\prime} \right] \]
Ahora, se puede calcular la energía total de membrana de la placa. Después de un largo álgebra, la expresión final es
\[U_m = \frac{C}{2} \left[ (1 − \nu^2 )u^2_o − 2(1 − \nu^2 ) \frac{\pi^2}{8} \frac{u_o}{a} w^2_o + (3 − 2\nu) \frac{\pi^4}{64} \frac{w^4_o}{a^2} \right] \]
La energía potencial total del sistema es
\[\prod (u_o, w_o) = U_b + U_m − P u_o \]
El equilibrio del sistema requiere que la primera variación de la energía potencial total se desvanezca\(\delta \prod (u_o, w_o) = 0\). Esto lleva a dos ecuaciones
\[\frac{\partial \prod}{\partial u_o} = 0 \rightarrow P = (1 − \nu^2 )C \left[ u_o − \frac{\pi^2}{8}\frac{w^2_o}{a}\right] \]
\[\frac{\partial \prod}{\partial w_o} = 0 \rightarrow 64 \left(\frac{\pi}{a}\right)^2 w_o \left[ \frac{4 \pi^2 D}{C} − (1 − \nu^2 )au_o + (3 − 2\nu) \frac{\pi^2}{8} w^2_o \right] = 0 \]
Hay dos soluciones del sistema anterior. La solución de prepandeo se recupera mediante fraguado\(w_o = 0\). Entonces de Ecuación (?? )
\[P = (1 − \nu^2 )Cu_o = (1 − \nu^2 ) \frac{Eh}{1 − \nu^2} u_o = Ehu_o \label{11.44}\]
y Ecuación (?? ) se satisface de manera idéntica. La solución (?? ) es exacta y es igual a la derivada en la Sección 10.1 del Capítulo 10. En el rango post-pandeo\(w_o > 0\) y Ecuación (?? ) proporciona una relación única entre la amplitud en el plano y fuera del plano del supuesto campo de desplazamiento
\[\frac{\pi^2}{8}\left(\frac{w_o}{a}\right)^2 = \frac{1 - \nu^2}{3 - 2\nu} \frac{u_o}{a} - \frac{4 D \pi^2}{C(3-2\nu) a^2} \]
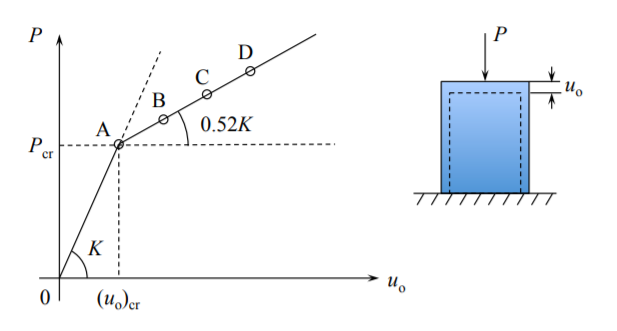
La gráfica de la función\(w_o = w_o(u_o)\) se muestra en la Figura (\(\PageIndex{2}\)).
El desplazamiento crítico\((u_o)_c\) a la hebilla, correspondiente al punto de pandeo, se obtiene de la Ecuación (?? ) por ajuste\(w_o = 0\)
\[(u_o)_c = \frac{4\pi^2D}{a} \frac{1}{C(1 − \nu^2)} \]

Eliminando\(w_o\) entre Ecuaciones (?? ) y (?? ) da una solución lineal post-pandeo
\[P = \frac{13}{25} (1 − \nu^2 )Cu_o + \frac{1 − \nu^2}{3 − 2\nu}\frac{4\pi^2 D}{a} \]
La rigidez posterior al pandeo\(K_{\text{post}} = \frac{dD}{du_o}\) es
\[K_{\text{post}} = \frac{13}{25} (1 − \nu^2)C = 0.52K_{\text{pre}}\]
donde\(K_{\text{pre}}\) esta la rigidez pre-pandeo. Para todos los fines prácticos se puede suponer que la placa está perdiendo la mitad de su rigidez después del pandeo pero es capaz de soportar cargas adicionales. Con base en el análisis anterior, la relación carga-desplazamiento de una placa elástica se representa en la Figura (\(\PageIndex{3}\)).
Sustituyendo la expresión por\((u_o)_c\) en la ecuación\ ref {11.44}, la carga de pandeo prevista es
\[P_c = \frac{4\pi^2D}{a}\]
que es la solución exacta del problema.


