10.6: Resistencia máxima de las placas
- Page ID
- 85269
En el apartado anterior hemos demostrado que después de pandeo la placa sigue tomando carga adicional pero con la mitad de su rigidez pre-pandeo. Para entender lo que sucede a continuación, examinemos la distribución de las tensiones de compresión en el plano\(\sigma_{xx}\) en\(x = a\). De Ecuaciones (10.2.10-10.2.11) y (?? ) los componentes\(\sigma_{xx}\)
\[\sigma_{xx}(y) = \frac{N_{xx}}{h} = \frac{E}{1 − \nu^2} \left[ −(1 − \nu^2) \frac{u_o}{a} + \frac{\pi^2}{2} \left(\frac{w_o}{a} \right)^2 \sin^2 \frac{\pi y}{a} \right] \]
El primer término representa tensión negativa, compresiva, uniforme a lo largo del ancho de la placa. El segundo término describe el alivio de la tensión de tracción producida por la rotación finita. La relación entre\(w_o\) y\(u_o\) está dada por la Ecuación (?? ) y se representa en la Figura (10.5.2). En la Figura (\(\PageIndex{1}\)) se muestra una gráfica de la función\(\sigma_{xx}(y)\) para varios valores del parámetro\(u_o\) similar al tiempo. Obsérvese que las curvas etiquetadas A, B, C y D corresponden a los puntos respectivos en las Figs. (10.5.2) y (10.5.3).
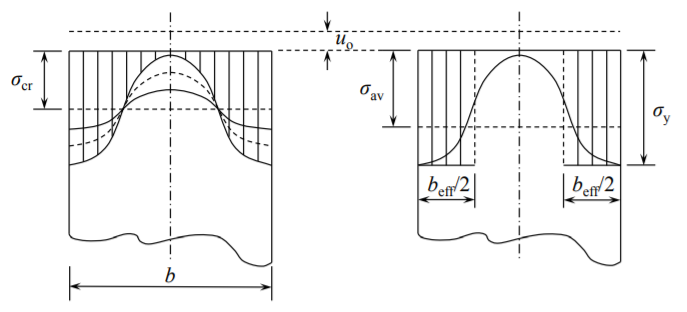
Con el aumento de la compresión de la placa hay una redistribución de tensiones a lo largo del borde cargado\(x = 0\) y\(x = a\). La tensión en el borde descargado\(y = 0\) y\(y = a\) sigue aumentando mientras que la tensión en el plano de simetría de la placa\(y = \frac{a}{2}\) disminuye a cero.
Fue el científico e ingeniero alemán, Theodore von Karman quien en 1932 hizo uso de la observación presentada en la Figura (\(\PageIndex{1}\)). Supuso que la parte central, descargada de la placa lleva cero esfuerzos mientras que la zona de borde, cada uno de los anchos\(b_{\text{eff}}/2\) alcanza el límite elástico en el punto de carga final. Como punto de partida, von Karman utilizó la expresión para la carga crítica de pandeo\(N_c\) y observó la relación entre la tensión en el borde cargado\(\sigma_e\) y el ancho de la placa\(b\)
\[\sigma_e = \frac{N_e}{h} = \frac{N_c}{h} = \frac{4\pi^2D}{hb^2} = \frac{4\pi^2Eh^2}{12(1 − \nu^2)b^2} = 1.9^2E\left(\frac{h}{b}\right)^2\]
Normalmente\(b\) es el parámetro de entrada y la tensión\(\sigma_e\) es una cantidad desconocida. El ingenio de von Karman fue que invirtió lo que se sabe y se desconoce en Ecuación (?? ). Preguntó cuál debería ser el ancho de la placa\(b_{\text{eff}}\) para que el esfuerzo del borde alcance el límite elástico. Por lo tanto
\[\sigma_y = 1.9^2E\left(\frac{h}{b_{\text{eff}}}\right)^2\]
Resolviendo la ecuación anterior para\(b_{\text{eff}}\)
\[b_{\text{eff}} = 1.9h \sqrt{\frac{E}{\sigma_y}}\]
Tomando por ejemplo\(E = 200000\) MPa,\(b_{\text{eff}}\sigma_y = 320\) MPa, el ancho efectivo se vuelve
\[b_{\text{eff}} = 1.9h \sqrt{625} = 47.5h \]
El ancho efectivo depende del módulo de Young y el límite elástico es proporcional al grosor de la placa. Aproximadamente 40-50 espesores de la placa cerca de los bordes lleva la carga, la parte central restante no es efectiva. La carga total en la placa se puede expresar de dos maneras
\[P_{\text{ult}} = b_{\text{eff}} \cdot \sigma_y = b \cdot \sigma_{\text{av}}\]
donde\(\sigma_{\text{av}} = \sigma_{\text{ult}}\) es el esfuerzo promedio en el borde cargado en el punto de resistencia final,
\[\frac{\sigma_{\text{av}}}{\sigma_{\text{ult}}} = \frac{b_{\text{eff}}}{b} = 1.9 \frac{h}{b} \sqrt{\frac{E}{\sigma_y}}\]
El grupo de parámetros
\[\beta = \frac{b}{h} \sqrt{\frac{\sigma_y}{E}}\]
se conoce como la relación de esbeltez de la placa. Tenga en cuenta que este es un concepto diferente al de la relación de esbeltez de la columna\(l/\rho\). Usando el parámetro\(\beta\), la resistencia final de la placa normalizada por el límite elástico es
\[\frac{\sigma_{\text{ult}}}{\sigma_{y}} = \frac{1.9}{\beta}\]
Recordemos que la tensión normalizada de pandeo de la placa elástica es
\[\frac{\sigma_{\text{cr}}}{\sigma_{y}} = \left(\frac{1.9}{\beta}\right)^2\]
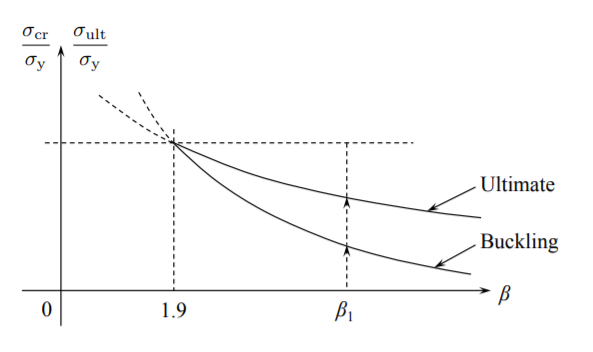
Las gráficas de ambas funciones se muestran en la Figura (\(\PageIndex{2}\)).
A partir de esta figura se puede identificar la relación crítica de esbeltez
\[\beta_{\text{cr}} = 1.9 \]
cuando tanto la carga final como la carga crítica de pandeo alcanzan el rendimiento. De la Ecuación (?? ) se puede ver que en\(\beta = \beta_{\text{cr}}\), el ancho efectivo es igual al ancho de la placa,\(b_{\text{eff}} = b\).
Eliminando el parámetro\(\beta\) entre Ecuaciones (?? ) y (?? ), se considera que el esfuerzo final es el promedio geométrico entre el límite elástico y el esfuerzo crítico de pandeo
\[\sigma_{\text{ult}} = \sqrt{\sigma_{\text{cr}} \cdot \sigma_{y}}\]
Por ejemplo, la carga continua de una placa con la relación de esbeltez primero\(\beta_1\) encontrará la curva de pandeo y luego la curva de resistencia final, como se ilustra en la Figura (\(\PageIndex{2}\)). El análisis anterior fue válido para placas simplemente soportadas a lo largo de los cuatro bordes, para los cuales es el coeficiente de pandeo\(k_c = 4\). Para otro tipo de soporte Ecuación (?? ) sigue siendo válido con el coeficiente 1.9 sustituido por 1.9\(\frac{k_c}{4}\).
En el pasado se ha dedicado mucho esfuerzo para validar experimentalmente la predicción de la teoría del ancho efectivo de von Karman. Se encontró que una pequeña corrección a la Ecuación (?? ) proporciona un buen ajuste de la mayoría de los datos de prueba
\[\frac{\sigma_{\text{ult}}}{\sigma_{y}} = \frac{b_{\text{eff}}}{b} = \frac{1.9}{\beta} − \frac{0.9}{\beta^2}\]
Por ejemplo, para una relativamente corta (placa fornida)\(\beta = 2\beta_{\text{cr}} = 3.8\), la fórmula original sobrepredice en un 15% que la ecuación empírica más exacta (?? ). Para placas delgadas, la diferencia es pequeña. Este último ha sido la base para el diseño de elementos compresivos de pared delgada en la mayoría de los estándares nacionales e internacionales como AISI, Aluminum Association y AISC.


