3.3: Transformaciones tensoras
- Page ID
- 83310
Introducción
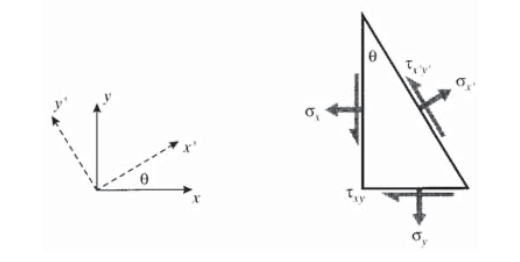
Uno de los problemas más comunes en mecánica de materiales implica la transformación de ejes. Por ejemplo, podemos conocer las tensiones que actúan sobre\(xy\) los planos, pero realmente estamos más interesados en las tensiones que actúan sobre planos orientados, digamos, en 30\(^{\circ}\) al\(x\) eje como se ve en la Figura 1, tal vez porque estos son planos atómicos muy empaquetados en los que es propenso a ocurrir el deslizamiento, o es el ángulo en el que se pegan dos piezas de madera en una articulación de “bufanda”. Buscamos un medio para transformar las tensiones a estos nuevos\(x'y'\) planos.
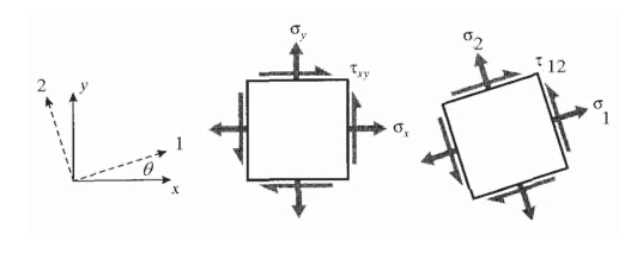
Estas transformaciones son vitales en los análisis de tensión y deformación, tanto porque son necesarias para calcular valores críticos de estas entidades como también porque la naturaleza tensorial del estrés y la deformación se ve más claramente en sus propiedades de transformación. Otras entidades, como el momento de inercia y curvatura, también se transforman de manera similar a la tensión y la deformación. Todos estos son tensores de segundo rango, un concepto importante que se esbozará más adelante en este módulo.
Enfoque directo
Las reglas para las transformaciones de estrés se pueden desarrollar directamente a partir de consideraciones de equilibrio estático. Para ilustración, considere el caso de la tensión uniaxial mostrada en la Figura 2 en la que todas las tensiones distintas a\(\sigma_y\) las cero. Luego se construye un diagrama de cuerpo libre en el que el espécimen se “corta” a lo largo del plano inclinado en el que se desean las tensiones\(\tau_{x'y'}\), etiquetadas\(\sigma_{y'}\) y,. La clave aquí es señalar que el área sobre la que actúan estas tensiones transformadas es diferente al área normal al eje y, por lo que tanto las áreas como las fuerzas que actúan sobre ellas necesitan ser “transformadas”. Equilibrar las fuerzas en la\(y'\) dirección (la dirección normal al plano inclinado):
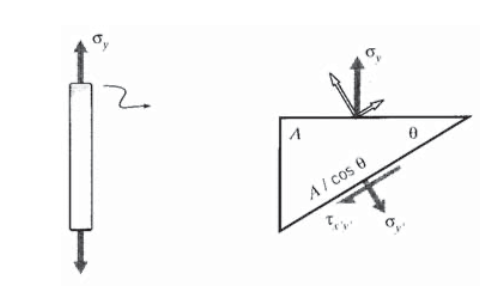
\((\sigma_y A) \cos \theta = \sigma_{y'} \left (\dfrac{A}{\cos \theta} \right )\)
\[\sigma_{y'} = \sigma_y \cos^2 \theta\]
Del mismo modo, un equilibrio de fuerzas en la dirección tangencial da
\[\tau_{x'y'} = \sigma_y \sin \theta \cos \theta\]
Ejemplo\(\PageIndex{1}\)
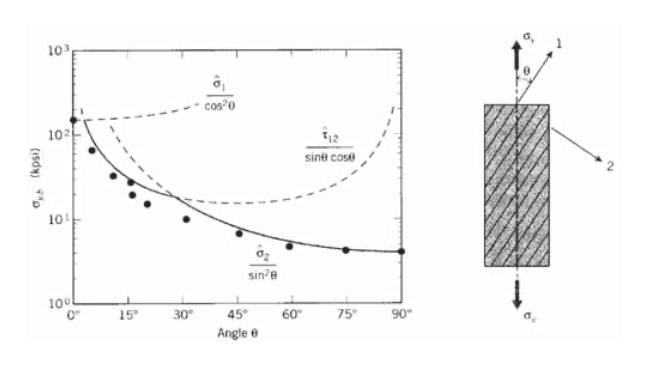
Considere una capa compuesta reforzada unidireccionalmente con resistencias\(\hat{\sigma}_1\) en la dirección de la fibra,\(\hat{\sigma}_2\) en la dirección transversal y\(\hat{\tau}_{12}\) en cizallamiento. A medida que aumenta el ángulo\(\theta\) entre la dirección de la fibra y una tensión\(\sigma_y\) de tracción aplicada, la tensión en la dirección de la fibra disminuirá de acuerdo con la Ecuación 3.3.1. Si la capa fallara solo por fractura de fibra, la tensión\(\sigma_{y, b}\) necesaria para causar falla aumentaría con la desalineación según\(\sigma_{y, b} = \hat{\sigma}_1/\cos^2 \theta\).
Sin embargo, las tensiones cortantes dadas por la Ecuación 3.3.2 aumentan con\(\theta\), por lo que la tensión σy necesaria para la falla por cizallamiento disminuye. La resistencia\(\sigma_{y,b}\) es la menor de las tensiones necesarias para causar fallas en la dirección de la fibra o por cizallamiento, por lo que la resistencia se ve limitada por el cizallamiento después de solo unos pocos grados de desalineación. De hecho, se ha propuesto un espécimen de tracción\(^{\circ}\) fuera del eje 15 como medio para medir la resistencia al cizallamiento intralaminar. Cuando el ángulo de orientación se aproxima a 90\(^{\circ}\), la falla está dominada por la resistencia transversal. Los datos experimentales que se muestran en la Figura 3 son para compuestos vidrio-epoxi (R.M. Jones, Mechanics of Composite Materials, McGraw-Hill, 1975.), los cuales muestran una concordancia buena pero no exacta con estas expresiones simples.
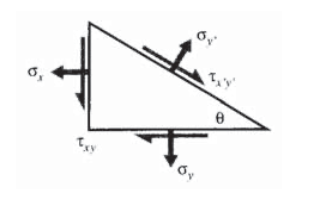
Un enfoque similar, pero generalizado para incluir tensiones\(\sigma_x\) y\(\tau_{xy}\) en los\(xy\) planos originales como se muestra en la Figura 4 (ver Ejercicio\(\PageIndex{2}\)) da:
\[\begin{array} {rcl} {\sigma_{x'}} & = & {\sigma_x \cos^2 \theta + \sigma_y \sin^2 \theta + 2 \tau_{xy} \sin \theta \cos \theta} \\ {\sigma_{y'}} & = & {\sigma_x \sin^2 \theta + \sigma_y \cos^2 \theta - 2 \tau_{xy} \sin \theta \cos \theta} \\ {\tau_{x'y'}} & = & {(\sigma_y - \sigma_x) \sin \theta \cos \theta + \tau_{xy} (\cos^2 \theta - \sin^2 \theta)} \end{array}\]
Estas relaciones se pueden escribir en forma de pseudovector-matriz como
\[\left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\tau_{x'y'}} \end{array} \right \} = \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\tau_{xy}} \end{array} \right \}\]
dónde\(c = \cos \theta\) y\(s = \sin \theta\). Esto se puede abreviar como
\[\sigma'=A \sigma\]
donde\(A\) está la matriz de transformación entre paréntesis arriba. Esta expresión sería válida tanto para estados de tensión tridimensionales como bidimensionales, aunque la forma particular de\(A\) dada en la Ecuación 3.3.4 es válida solo en dos dimensiones (tensión plana), y para coordenadas cartesianas.
Utilizando argumentos matemáticos o geométricos (ver Ejercicio\(\PageIndex{3}\) y Ejercicio\(\PageIndex{4}\)), se puede demostrar que los componentes de la deformación infinitesimal se transforman casi por las mismas relaciones:
\[\left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\dfrac{1}{2} \gamma_{x'y'}} \end{array} \right \} = A \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\dfrac{1}{2} \gamma_{xy}} \end{array} \right \}\]
El factor de 1/2 en los componentes de cizallamiento surge de la definición clásica de deformación por cizallamiento, que es el doble de la tensión de cizallamiento tensorial. Esto introduce cierta torpeza en las relaciones de transformación, algunas de las cuales pueden reducirse definiendo la matriz de Reuter como
\[[R] = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \ \ or \ \ [R]^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \tfrac{1}{2} \end{bmatrix}\]
Ahora podemos escribir:
\[\left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\gamma_{x'y'}} \end{array} \right \} = R \left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\dfrac{1}{2} \gamma_{x'y'}} \end{array} \right \} = RA \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\dfrac{1}{2} \gamma_{xy}} \end{array} \right \} = RAR^{-1} \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\gamma_{xy}} \end{array} \right \} \nonumber\]
O
\[\epsilon' = RAR^{-1} \epsilon\]
Como se puede verificar expandiendo esta relación, las ecuaciones de transformación para deformación también se pueden obtener a partir de las ecuaciones de transformación de tensión (por ejemplo, Ecuación 3.3.3) reemplazando\(\sigma\) con\(\epsilon\) y\(\tau\) con\(\gamma /2\):
\[\begin{array} {rcl} {\epsilon_{x'}} & = & {\epsilon_x \cos^2 \theta + \epsilon_y \sin^2 \theta + \gamma_{xy} \sin \theta \cos \theta} \\ {\epsilon_{y'} & = & {\epsilon_x \sin^2 \theta + \epsilon_y \cos^2 \theta - \gamma_{xy} \sin \theta \cos \theta} \\ {\gamma_{x'y'}} & = & {2 (\epsilon_y - \epsilon_x) \sin \theta \cos \theta + \gamma_{xy} (\cos^2 \theta - \sin^2 \theta)} \end{array}\]
Ejemplo\(\PageIndex{2}\)
Considerar el estado de deformación biaxial
\[\epsilon = \left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\gamma_{x'y'}} \end{array} \right \} = \left \{\begin{array} {c} {0.01} \\ {-0.01} \\ {0} \end{array} \right \} \nonumber\]
El estado de deformación\(\epsilon'\) referido a los ejes girados\(\theta = 45^{\circ}\) desde los\(x-y\) ejes se puede calcular por multiplicación matricial como:
\[A = \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} = \begin{bmatrix} 0.5 & 0.5 & 1.0 \\ 0.5 & 0.5 & -1.0 \\ -0.5 & 0.5 & 0.0 \end{bmatrix} \nonumber\]
Entonces
\[\epsilon' = RAR^{-1} \epsilon \nonumber\]
\[\begin{bmatrix} 1.0 & 1.0 & 0.0 \\ 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 2.0 \end{bmatrix} \begin{bmatrix} 0.5 & 0.5 & 1.0 \\ 0.5 & 0.5 & -1.0 \\ -0.5 & 0.5 & 0.0 \end{bmatrix} \begin{bmatrix} 1.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.5 \end{bmatrix} = \left \{\begin{array} {c} {0.00} \\ {0.00} \\ {-0.02} \end{array} \right \}\nonumber\]
Obviamente, el método de multiplicación matricial es tedioso a menos que se disponga de software de manejo de matrices, en cuyo caso se vuelve muy conveniente.
Círculo de Mohr
La experiencia cotidiana con ocurrencias tan comunes como empujar objetos en ángulo nos da a todos un cierto sentido intuitivo de cómo funcionan las transformaciones vectoriales. Las transformaciones de tensores de segundo rango parecen más abstractas al principio, y un dispositivo para ayudar a visualizarlas es de gran valor. Al igual que sucede, las ecuaciones de transformación tienen una famosa interpretación gráfica (entre los ingenieros) conocida como círculo de Mohr (Presentado en 1900 por el ingeniero alemán Otto Mohr (1835—1918).). El procedimiento Mohr se justifica matemáticamente mediante el uso de las relaciones trigonométricas de doble ángulo para mostrar que las Eqns. 3.3.3 tienen una representación circular (ver Ejercicio\(\PageIndex{5}\)), pero probablemente se pueda aprender mejor simplemente memorizando la siguiente receta (Una demostración web interactiva del círculo de Mohr construcción está disponible en < http://web.mit.edu/course/3/3.11/www/java/mohr.html >.).
- Dibuje el cuadrado de tensión, anotando los valores en las caras x e y; la Figura 5 (a) muestra un caso hipotético para ilustración. Solo con el propósito del círculo de Mohr, considere un esfuerzo cortante que actúa en un sentido de rotación en sentido horario como positivo, y en sentido contrario a las agujas del reloj como negativo. Las tensiones cortantes en las\(y\) caras\(x\) y deben tener signos opuestos. Las tensiones normales son positivas en tensión y negativas en compresión, como es habitual.
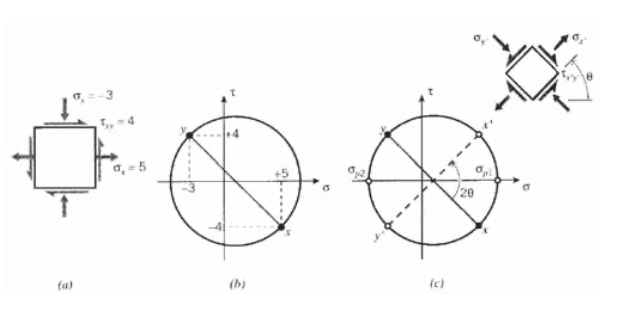
- Construir una gráfica con\(\tau\) como la ordenada (\(y\)eje) y\(\sigma\) como abscisas, y trazar las tensiones en las\(y\) caras\(x\) y del cuadrado de tensión como dos puntos en esta gráfica. Dado que las tensiones cortantes en estas dos caras son negativas entre sí, uno de estos puntos estará por encima del eje σexactamente hasta donde el otro esté por debajo. Es útil etiquetar los dos puntos como\(x\) y\(y\).
- Conecta estos dos puntos con una línea recta. Cruzará el\(\sigma\) eje en el punto medio de la línea. Este punto será at\((\sigma_x + \sigma_y)/2\), que en nuestra ilustración es [5 + (−3)] /2 = 1.
- Coloque la punta de una brújula en el punto medio de la línea y coloque el lápiz al final de la línea. Dibuja un círculo con la línea como un diámetro. El círculo completado para nuestro estado de estrés ilustrativo se muestra en la Figura 5 (b).
- Para determinar las tensiones en un cuadrado de tensión que ha sido girado en un ángulo\(\theta\) con respecto al cuadrado original, gire la línea diametral en la misma dirección a través del doble de este ángulo; es decir\(2\theta\). Ahora se pueden etiquetar los nuevos puntos finales de la línea\(x'\) y\(y'\), y sus\(\sigma - \tau\) valores son las tensiones en los\(x'-y'\) ejes girados como se muestra en la Figura 5 (c).
No hay nada misterioso ni mágico en el círculo de Mohr; es simplemente un dispositivo para ayudar a visualizar cómo cambian las tensiones y otros tensores de segundo rango cuando se rotan los ejes.
Es claro al observar el círculo de Mohr en la Figura 5 (c) que hay algo especial en las rotaciones de los ejes que hacen que la línea diametral se vuelva horizontal o vertical. En el primer caso, las tensiones normales asumen valores máximos y las tensiones cortantes son cero. Estas tensiones normales se conocen como las tensiones principales,\(\sigma_{p1}\) y\(\sigma_{p2}\), y los planos sobre los que actúan son los planos principales. Si el material es propenso a fallar por agrietamiento por tracción, lo hará agrietándose a lo largo de los planos principales cuando el valor de\(\sigma_{p1}\) exceda la resistencia a la tracción.
Ejemplo\(\PageIndex{3}\)
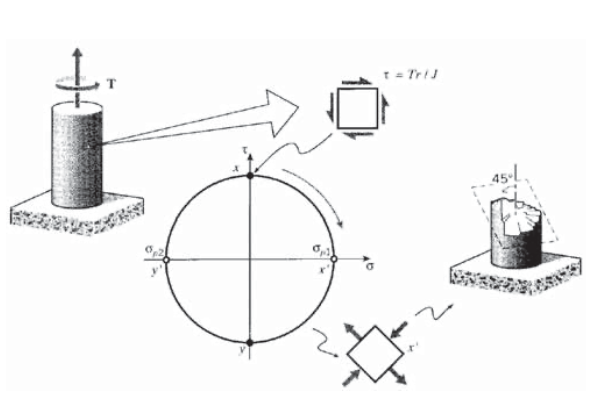
Es instructivo usar una construcción de círculo de Mohr para predecir cómo un trozo de tiza de pizarra se romperá en torsión, y luego verificarlo en la práctica. La torsión produce un estado de cizallamiento puro como se muestra en la Figura 6, lo que hace que los planos principales aparezcan en\(\pm 45^{\circ}\) el eje largo de la tiza. La grieta aparecerá transversal a la tensión de tracción principal, produciendo una superficie de falla similar a la espiral. (A medida que la grieta avanza hacia la tiza, el estado de cizallamiento puro se reemplaza por una distribución de tensión más complicada, por lo que la última parte de la superficie de falla se desvía de esta trayectoria ideal a una que corre a lo largo de la dirección axial). Este es el mismo tipo de fractura que se produjo con demasiada frecuencia en los fémures de los esquiadores, antes de la llegada de las modernas fijaciones de seguridad.
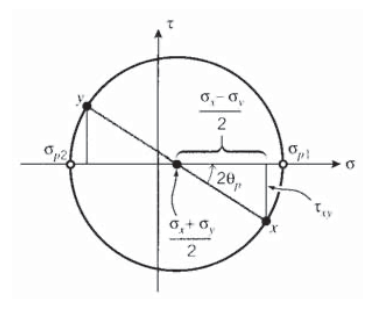
Por construcción pitagórica directa como se muestra en la Figura 7, el círculo de Mohr muestra que el ángulo desde los\(x-y\) ejes hasta los planos principales es
\[\tan 2 \theta_p = \dfrac{\tau_{xy}}{(\sigma_x - \sigma_y)/2}\]
y los valores de las tensiones principales son
\[\sigma_{p1,p1} = \dfrac{\sigma_x + \sigma_y}{2} \pm \sqrt{(\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2}\]
donde el primer término anterior es la\(\sigma\) coordenada del centro del círculo, y el segundo es su radio.
Cuando la línea diametral del círculo de Mohr es vertical, las tensiones cortantes se vuelven máximas, iguales en magnitud al radio del círculo:
\[\tau_{\max} = \sqrt{(\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2} = \dfrac{\sigma_{p1} - \sigma_{p2}}{2}\]
Los puntos de cizallamiento máximo están\(^{\circ}\) a 90 de los puntos de tensión principales en el círculo de Mohr, por lo que en el espécimen real los planos de cizallamiento máximo están\(^{\circ}\) a 45 de los planos principales. El deslizamiento molecular asociado con el rendimiento es impulsado por cizallamiento, y generalmente tiene lugar en los planos de cizallamiento máximo. Una muestra de tracción tiene planos principales a lo largo y transversal a su dirección de carga, por lo que el deslizamiento por cizallamiento ocurrirá en los planos\(\pm\) 45\(^{\circ}\) desde la dirección de carga. Estos planos de deslizamiento a menudo se pueden observar como “bandas de cizallamiento” en el espécimen.
Tenga en cuenta que las tensiones normales pueden aparecer en los planos de cizallamiento máximo, por lo que la situación no es exactamente la inversa de los planos principales, en los que las tensiones cortantes desaparecen mientras que las tensiones normales son máximas. Si las tensiones normales desaparecen en los planos de cizallamiento máximo, se dice que el estado de tensión es uno de “cizallamiento puro”, tal como es inducido por torsión simple. Por lo tanto, un estado de cizallamiento puro es aquel para el que existe una rotación de ejes tal que las tensiones normales desaparecen, lo cual es posible solo si el centro del círculo de Mohr está en el origen, es decir\((\sigma_x + \sigma_y)/2 = 0\). De manera más general, un estado de cizallamiento puro es aquel en el que la traza de la matriz de tensión (y deformación) se desvanece.
Ejemplo\(\PageIndex{4}\)
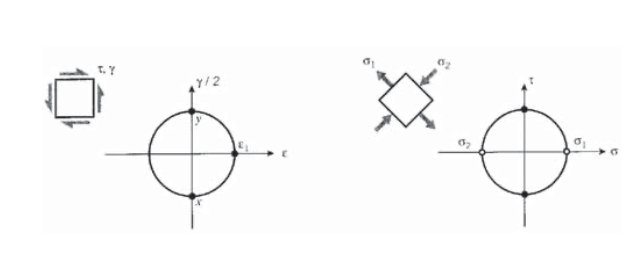
Los círculos de Mohr se pueden dibujar tanto para tensiones como para tensiones, con deformación cortante trazada en la ordenada y deformación normal en abscisas. Sin embargo, la ordenada debe ser\(\gamma/2\) más que justa\(\gamma\), debido a la forma en que se definen las cepas infinitesimales clásicas. Considere un estado de cizallamiento puro con deformación\(\gamma\) y esfuerzo\(\tau\) como se muestra en la Figura 8, tal como podría producirse colocando un eje circular en torsión. Un círculo de Mohr para la tensión muestra rápidamente la tensión principal, en un avión\(^{\circ}\) a 45 de distancia, es dada por\(\epsilon_1 = \gamma/2\). La ley de Hooke para cizalla da\(\tau = G \gamma\), entonces\(\epsilon_1 = \tau /2G\). La deformación principal también está relacionada con las tensiones principales por
\[\epsilon_1 = \dfrac{1}{E} (\sigma_2 - \nu \sigma_2)\nonumber\]
El círculo de Mohr para el estrés da\(\sigma_1 = -\sigma_2 = \tau\), así que esto se puede escribir
\[\dfrac{\tau}{2G} = \dfrac{1}{E} [\tau - \nu (-\tau)]\nonumber\]
Cancelando\(\tau\) y reordenando, tenemos la relación entre las constantes elásticas declaradas anteriormente sin pruebas:
\[G = \dfrac{E}{2(1 + \nu)} \nonumber\]
Planteamiento general
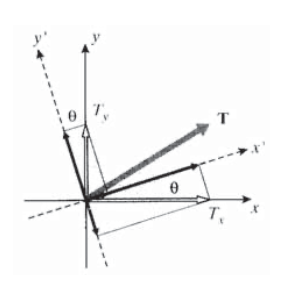
Otra aproximación a las ecuaciones de transformación de tensiones, capaces de extenderse fácilmente a tres dimensiones, comienza con las relaciones familiares mediante las cuales los vectores se transforman en dos dimensiones (ver Figura 9):
\[T_{x'} = T_x \cos \theta + T_y \sin \theta \nonumber\]
\[T_{y'} = -T_x \sin \theta + T_y \cos \theta \nonumber\]
En forma de matriz, es decir
\[\left \{ \begin{array} {c} {T_{x'}} \\ {T_{y'}} \end{array} \right \} = \begin{bmatrix} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{bmatrix} \left \{ \begin{array} {c} {T_{x}} \\ {T_{y}} \end{array} \right \} \nonumber\]
o
\[T' = aT\]
donde a es otra matriz de transformación que sirve para transformar los componentes vectoriales en el sistema de coordenadas original a los del sistema cebado. En términos de notación de índices, esto también podría denotarse\(a_{ij}\), de manera que
\[T_i' = a_{ij} T_j\nonumber\]
Los elementos individuales de aij son los cosenos de los ángulos entre el eje\(i^{th}\) cebado y el eje\(j^{th}\) no cebado.
Se puede demostrar por examen directo que la matriz a tiene la propiedad útil de que su inverso equivale a su transposición; es decir,\(a^{-1} = a^T\). Podemos multiplicar la Ecuación 3.3. 13 por\(a^T\) para dar
\[a^T T' = (a^T a) T = T\]
por lo que la transformación puede pasar de cebado a no cebado, o al revés.
Estas relaciones pueden extenderse para producir una expresión para la transformación de tensiones (o tensiones, o momentos de inercia, u otras cantidades similares). Recordemos la relación de Cauchy en forma de matriz:
\[[\sigma] \hat{n} = T\nonumber\]
Usando la Ecuación 3.3.14 para transformar los\(T\) vectores\(\hat{n}\) y en sus contrapartes cebadas, tenemos
\[[\sigma] a^T \hat{n}' = a^T T'\nonumber\]
Multiplicando a través de un:
\ ((a [\ sigma] a^t)\ hat {n} '= (AA^t) T' = T'\ nonumber\]
Esta es solo la relación de Cauchy nuevamente, pero en el marco de coordenadas cebado. Por lo tanto, la cantidad entre paréntesis debe ser\([\sigma']\):
\[[\sigma'] = a[\sigma] a^T\]
Por lo tanto, la transformación de tensiones y se puede hacer por pre y postmultiplicación por la misma matriz de transformación aplicable a la transformación vectorial. Esto también se puede escribir usando notación de índice, que proporciona otra ilustración de las diferencias de transformación entre escalares (tensores de rango cero), vectores (tensores de primer rango) y tensores de segundo rango:
\[\begin{array} {rcl} {\text{rank 0:}} & \ \ \ & {b' = b} \\ {\text{rank 1:}} & \ \ \ & {T_i' = a_{ij} T_j} \\ {\text{rank 2:}} & \ \ \ & {\sigma_{ij}' = a_{ij} a_{kl} \sigma_{kl}} \end{array}\]
En el trabajo práctico, no siempre es un asunto sencillo anotar los nueve elementos de la matriz a necesarios en la Ecuación 3.3.15. Los cuadrados de los componentes de\(\hat{n}\) para cualquier plano dado deben sumarse a la unidad, y para que los tres planos del cubo de tensión transformado sean mutuamente perpendiculares, el producto de punto entre cualquiera de dos normales planos debe desaparecer. Entonces no tendrán sentido los nueve números cualquiera. La obtención de una es mucho más fácil mediante el uso de “ángulos de Euler” para describir las transformaciones de ejes en tres dimensiones.
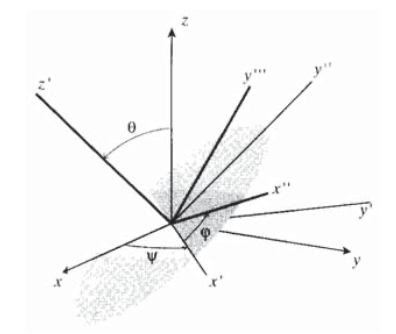
Como se muestra en la Figura 10, los ejes transformados finales se visualizan como logrados en tres pasos: primero, rotar los\(x-y-z\) ejes originales un ángulo\(\psi\) (psi) alrededor del\(z\) eje -eje para obtener un nuevo marco que podamos llamar\(x'-y'-z\). A continuación, rote este nuevo marco un ángulo\(\theta\) alrededor del\(x'\) eje para obtener otro fotograma al que podamos llamar\(x'-y''-z'\). Finalmente, gire este marco en un ángulo\(\phi\) (phi) alrededor del\(z'\) eje para obtener el marco final\(x''-y'''-z'\). Estas tres transformaciones corresponden a la matriz de transformación
\[a = \begin{bmatrix} \cos \psi & \sin \psi & 0 \\ -\sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & \sin \theta \\ 0 & -\sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{bmatrix} \nonumber\]
Esta multiplicación sin duda sería un dolor si se hiciera manualmente, pero es natural para un enfoque computacional.
Ejemplo\(\PageIndex{5}\)
El siguiente resultado muestra una evaluación por computadora de una transformación de estrés tridimensional, en este caso utilizando el software de matemáticas simbólicas MapleTM.
# read linear algebra library
> with(linalg):
# Define Euler-angle transformation matrices:
> a1:=array(1..3,1..3,[[cos(psi),sin(psi),0],[-sin(psi),cos(psi),0],[0,0 > ,1]]);
[cos(psi) sin(psi) 0]
a1 := [-sin(psi) cos(psi) 0]
[ 0 0 1]
> a2:=array(1..3,1..3,[[1,0,0],[0,cos(theta),sin(theta)],[0,-sin(theta),
> cos(theta)]]);
[1 0 0. ]
a2 := [0 cos(theta) sin(theta)]
[0. -sin(theta) cos(theta)]
> a3:=array(1..3,1..3,[[cos(phi),sin(phi),0],[-sin(phi),cos(phi),0],[0,0 > ,1]]);
[cos(phi) sin(phi) 0]
a3 := [-sin(phi) cos(phi) 0]
[ 0 0 1]
# Overall transformation matrix (multiply individual Euler matrices):
> a:=a1&*a2&*a3;
a := (a1 &* a2) &* a3
# Set precision and read in Euler angles (converted to radians); here
# we are rotating 30 degrees around the z axis only.
> Digits:=4;psi:=0;theta:=30*(Pi/180);phi:=0;
Digits := 4
psi := 0
theta := 1/6 Pi
phi := 0
# Display transformation matrix for these angles: "evalf" evaluates the
# matrix element, and "map" applies the evaluation to each element of
# the matrix.
> aa:=map(evalf,evalm(a));
[1. 0. 0. ]
aa := [0. .8660 .5000]
[0. -.5000 .8660]
# Define the stress matrix in the unprimed frame:
> sigma:=array(1..3,1..3,[[1,2,3],[2,4,5],[3,5,6]]);
[1 2 3]
sigma := [2 4 5]
[3 5 6]
# The stress matrix in the primed frame is then given by Equation 15:
> ’sigma_prime’=map(evalf,evalm(aa&*sigma&*transpose(aa)));
[1 3.232 1.598]
sigma_prime = [3.232 8.830 3.366]
[1.598 3.366 1.170]
Tensiones principales y planos en tres dimensiones
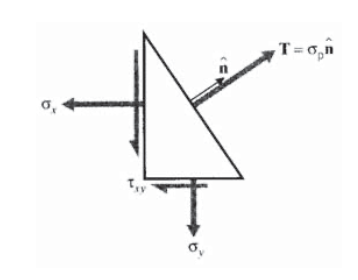
El procedimiento circular de Mohr no es capaz de encontrar tensiones principales para estados de estrés tridimensionales, y se necesita un método más general. En tres dimensiones, buscamos orientaciones de ejes de tal manera que no aparezcan esfuerzos cortantes, dejando solamente tensiones normales en tres direcciones ortogonales. La desaparición de esfuerzos cortantes en un plano significa que el vector de tensión\(T\) es normal al plano, ilustrado en dos dimensiones en la Figura 11. Por lo tanto, el vector de tracción puede escribirse como
\[T= \sigma_p \hat{n}\nonumber\]
donde\(\sigma_p\) es una cantidad escalar simple, la magnitud del vector de estrés. Usando esto en la relación de Cauchy:
\[\sigma \hat{n} = T = \sigma_p \hat{n}\nonumber\]
\[(\sigma - \sigma_p I) \hat{n} = 0\]
Aquí\(I\) está la matriz de unidades. Este sistema tendrá una solución no trivial (\(\hat{n} \ne 0\)) solo si su determinante es cero:
\[|\sigma - \sigma_p I| = \left | \begin{matrix} \sigma_x - \sigma_p & \tau_{xy} & \tau_{xz} \\ \tau_{xy} & \sigma_y - \sigma_p & \tau_{yz} \\ \tau_{xz} & \tau_{yz} & \sigma_z - \sigma_p \end{matrix} \right | = 0\nonumber\]
Al expandir el determinante se obtiene una ecuación polinómica cúbica en\(\sigma_p\):
\[f(\sigma_p) = \sigma_p^3 - I_1 \sigma_p^3 + I_2 \sigma_p - I_3 = 0\]
Esta es la ecuación característica para el estrés, donde los coeficientes son
\[I_1 = \sigma_x + \sigma_y + \sigma_z = \sigma_{kk}\]
\[I_2 = \sigma_x \sigma_y + \sigma_x \sigma_z + \sigma_y \sigma_z - \tau_{xy}^2 - \tau_{yz}^2 - \tau_{xz}^2 = \dfrac{1}{2} (\sigma_{ii} \sigma_{jj} - \sigma_{ij} \sigma_{ij})\]
\[I_3 = \text{det} |\sigma| = \dfrac{1}{3} \sigma_{ij} \sigma_{jk} \sigma_{ki}\]
Estos\(I\) parámetros se conocen como los invariantes del estado de tensión; no cambian con la transformación de las coordenadas y pueden ser utilizados para caracterizar la naturaleza general del estrés. Por ejemplo\(I_1\), que se ha identificado anteriormente como la traza de la matriz de tensión, se verá en una sección posterior como una medida de la tendencia del estado de tensión a inducir dilatación hidrostática o compresión. Ya hemos señalado que el estado de tensión es uno de cizallamiento puro si su rastro desaparece.
Dado que la ecuación característica es cúbica en\(\sigma_p\), tendrá tres raíces, y se puede demostrar que las tres raíces deben ser reales. Estas raíces son solo las principales tensiones\(\sigma_{p1}\),\(\sigma_{p2}\) y\(\sigma_{p3}\).
Ejemplo\(\PageIndex{6}\)
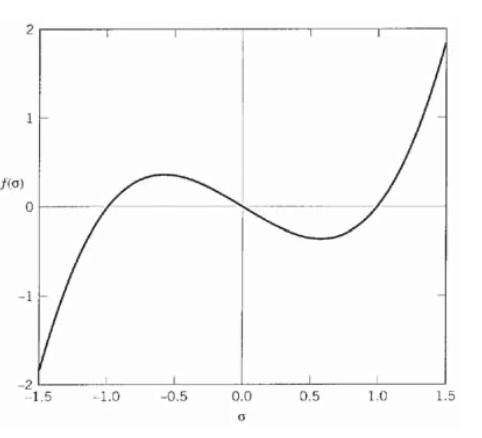
Considere un estado de cizallamiento simple con\(\tau_{xy} = 1\) y todas las demás tensiones cero:
\[|\sigma| = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\nonumber\]
Los invariantes son
\[I_1 = 0, I_2 = -1, I_3 = 0\nonumber\]
y la ecuación característica es
\[\sigma_p^3 - \sigma_p = 0\nonumber\]
Esta ecuación tiene raíces de (-1, 0, 1) correspondientes a tensiones principales\(\sigma_{p1} = 1, \sigma_{p2} = 0, \sigma_{p3} = -1\), y se grafica en la Figura 12. Este es el mismo estado de estrés considerado en el Ejemplo 4, y las raíces de la ecuación característica concuerdan con los valores principales mostrados por el círculo de Mohr.
Ejercicio\(\PageIndex{1}\)
Desarrollar una expresión de la tensión necesaria para causar falla transversal en un compuesto orientado unidireccionalmente en función del ángulo entre la dirección de carga y la dirección de la fibra, y mostrar esta función en una gráfica de resistencia versus\(\theta\).
Ejercicio\(\PageIndex{2}\)
Utilice un equilibrio de fuerzas de cuerpo libre para derivar las ecuaciones de transformación de tensiones cartesianas bidimensionales como
\[\begin{array} {rcl} {\sigma_{x'}} & = & {\sigma_x \cos^2 \theta + \sigma_y \sin^2 \theta + 2 \tau_{xy} \sin \theta \cos \theta} \\ {\sigma_{y'}} & = & {\sigma_x \sin^2 \theta + \sigma_y \cos^2 \theta - 2 \tau_{xy} \sin \theta \cos \theta} \\ {\tau_{x'y'}} & = & {(\sigma_y - \sigma_x) \sin \theta \cos \theta + \tau_{xy} (\cos^2 \theta - \sin^2 \theta)} \end{array} \nonumber\]
O
\[\left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\tau_{x'y'}} \end{array} \right \} = \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\tau_{xy}} \end{array} \right \}\nonumber\]
dónde\(c = \cos \theta\) y\(s = \sin \theta\)
Ejercicio\(\PageIndex{3}\)
Desarrollar relaciones matemáticas para desplazamientos y gradientes a lo largo de ejes transformados de la forma
\[u' = u \cos \theta + v \sin \theta \nonumber\]
\[\dfrac{\partial}{\partial x'} = \dfrac{\partial}{\partial x} \cdot \dfrac{\partial x}{\partial x'} + \dfrac{\partial}{\partial y} \cdot \dfrac{\partial y}{\partial x'} = \dfrac{\partial}{\partial x} \cdot \cos \theta + \dfrac{\partial}{\partial y} \cdot \sin \theta \nonumber\]
con expresiones análogas para\(v'\) y\(\partial /\partial y'\). Utilízalas para obtener las ecuaciones de transformación de deformación (Ecuación 3.3.6).
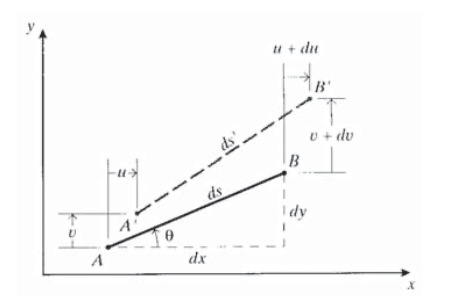
Ejercicio\(\PageIndex{4}\)
Considere un segmento\(AB\) de línea de longitud\(ds^2 = dx^2 + dy^2\), orientado en ángulo\(\theta\) desde los\(x - y\) ejes cartesianos como se muestra. Deje que el desplazamiento diferencial del extremo\(B\) relativo al extremo\(A\) sea
\[du = \dfrac{\partial u}{\partial x} dx + \dfrac{\partial u}{\partial y} dy\nonumber\]
\[dv = \dfrac{\partial v}{\partial x} dx + \dfrac{\partial v}{\partial y} dy\nonumber\]
Utilice esta geometría para derivar las ecuaciones de transformación de deformación (Ecuación 3.3.6), donde el\(x'\) eje está a lo largo de la línea\(AB\).
Ejercicio\(\PageIndex{5}\)
Emplear relaciones trigonométricas de doble ángulo para mostrar que las ecuaciones de transformación de tensiones cartesianas bidimensionales se pueden escribir en la forma
\[\begin{array} {rcr} {\sigma_{x'}} & = & {\tfrac{\sigma_x + \sigma_y}{2} + \tfrac{\sigma_x - \sigma_y}{2} \cos 2 \theta + \tau_{xy} \sin 2 \theta} \\ {\tau_{x'y'}} & = & {-\tfrac{\sigma_x - \sigma_y}{2} \sin 2 \theta + \tau_{xy} \cos 2\theta} \\ {\sigma_{y'}} & = & {\tfrac{\sigma_x + \sigma_y}{2} + \tfrac{\sigma_x - \sigma_y}{2} \cos 2 \theta - \tau_{xy} \sin 2 \theta} \end{array} \nonumber\]
Utilice estas relaciones para justificar la construcción del círculo Mohr.
Ejercicio\(\PageIndex{6}\)
Utilice la multiplicación matricial (Eqns. 3.3.5 o 3.3.8) para transformar los siguientes estados de tensión y deformación a ejes girados por\(\theta = 30^{\circ}\) de los\(x-y\) ejes originales.
(a)
\[\sigma = \left \{ \begin{array} {c} {1.0} \\ {-2.0} \\ {3.0} \end{array} \right \}\nonumber\]
b)
\[\epsilon = \left \{ \begin{array} {c} {0.01} \\ {-0.02} \\ {0.03} \end{array} \right \}\nonumber\]
Ejercicio\(\PageIndex{7}\)
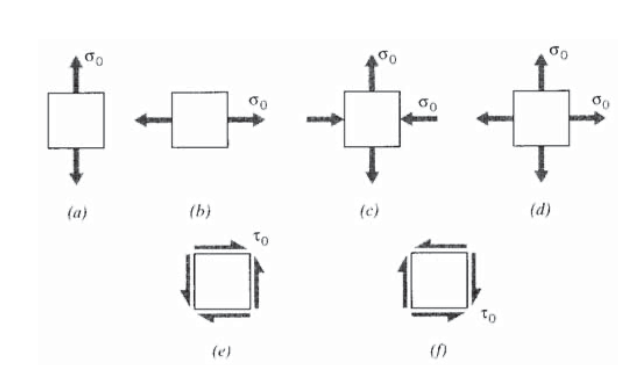
Esboce los círculos de Mohr para cada uno de los estados de estrés que se muestran en la siguiente figura.
Ejercicio\(\PageIndex{8}\)
Construir soluciones de círculo de Mohr para las transformaciones del Ejercicio\(\PageIndex{6}\).
Ejercicio\(\PageIndex{9}\)
Dibujar los círculos de Mohr y determinar las magnitudes de las tensiones principales para los siguientes estados de estrés. Denote el estado de tensión principal en un cuadrado de tensión adecuadamente girado.
(a)\(\sigma_x = 30\) MPa,\(\sigma_y = -10\) MPa,\(\tau_{xy} = 25\) MPa.
(b)\(\sigma_x = -30\) MPa,\(\sigma_y = -90\) MPa,\(\tau_{xy} = -40\) MPa.
(c)\(\sigma_x = -10\) MPa,\(\sigma_y = 20\) MPa,\(\tau_{xy} = -15\) MPa.
Ejercicio\(\PageIndex{10}\)
Mostrar que los valores de las tensiones principales dadas por el círculo de Mohr concuerdan con los obtenidos matemáticamente estableciendo a cero las derivadas de la tensión con respecto al ángulo de transformación.
Ejercicio\(\PageIndex{11}\)
Para el estado de tensión tridimensional\(\sigma_x = 25, \sigma_y = -15, \sigma_z = -30, \tau_{yz} = 20, \tau_{xz} = 10, \tau_{xy} = 30\) (todo en MPa):
(a) Determinar el estado de tensión para los ángulos de Euler\(\psi = 20^{\circ}\),\(\theta = 30^{\circ}\),\(\phi = 25^{\circ}\).
(b) Trazar la ecuación característica.
c) Determinar las tensiones principales.


