3.4: Relaciones constitutivas
- Page ID
- 83304
Introducción
Los módulos sobre cinemática (Módulo 8), equilibrio (Módulo 9) y transformaciones tensoras (Módulo 10) contienen conceptos vitales para la Mecánica de Materiales, pero no proporcionan información sobre el papel del material en sí. Las ecuaciones cinemáticas relacionan las deformaciones con los gradientes de desplazamiento, y las ecuaciones de equilibrio relacionan la tensión con las tracciones aplicadas en los límites cargados y también gobiernan las relaciones entre los gradientes de tensión dentro del material. En tres dimensiones hay seis ecuaciones cinemáticas y tres ecuaciones de balance, para un total de nueve. Sin embargo, hay quince variables: tres desplazamientos, seis cepas y seis tensiones. Necesitamos seis ecuaciones más, y estas son proporcionadas por las relaciones consitutivas del material: seis expresiones que relacionan las tensiones con las cepas. Se trata de una especie de ecuación mecánica de estado, y describen cómo se constituye mecánicamente el material.
Con estas relaciones constitutivas, se reafirma el papel vital del material: Las constantes elásticas que aparecen en este módulo son propiedades del material, sujetas a control por procesamiento y modificación microestructural como se describe en el Módulo 2. Esta es una herramienta importante para el ingeniero, y señala la necesidad de considerar el diseño del material así como con el material.
Materiales elásticos isotrópicos
En el caso general de una relación lineal entre los componentes de los tensores de tensión y tensión, podríamos proponer una declaración de la forma
\[\epsilon_{ij} = S_{ijkl} \sigma_{kl}\nonumber\]
donde el\(S_{ijkl}\) es un tensor de cuarto rango. Esto constituye una secuencia de nueve ecuaciones, ya que cada componente de\(\epsilon_{ij}\) es una combinación lineal de todos los componentes de\(\sigma_{ij}\). Por ejemplo:
\[\epsilon_{23} = S_{2311} \sigma_{11} + S_{2312} \sigma_{12} + \cdots + S_{2333} \epsilon_{33}\nonumber\]
Con base en cada uno de los índices de\(S_{ijkl}\) toma de valores de 1 a 3, podríamos esperar un total de 81 componentes independientes en\(S\). Sin embargo, ambos\(\epsilon_{ij}\) y\(\sigma_{ij}\) son simétricos, con seis en lugar de nueve componentes independientes cada uno. Esto reduce el número de\(S\) componentes a 36, como puede verse a partir de una relación lineal entre las formas pseudovectoriales de la deformación y el estrés:
\[\left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right \} = \begin{bmatrix} S_{11} & S_{12} & \cdots & S_{16} \\ S_{21} & S_{22} & \cdots & S_{26} \\ \cdots & \cdots & \cdots & \cdots \\ S_{61} & S_{62} & \cdots & S_{66} \end{bmatrix} \left \{ \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \tau_{yz} \\ \tau_{xz} \\ \tau_{xy} \end{matrix} \right \}\]
Se puede demostrar (G.M. Mase, Schaum's Outline of Theory and Problems of Continuum Mechanics, McGraw-Hill, 1970.) que la\(S\) matriz en esta forma también es simétrica. Por lo tanto, contiene sólo 21 elementos independientes, como se puede apreciar contando los elementos en el triángulo superior derecho de la matriz, incluyendo los elementos diagonales (1 + 2 + 3 + 4 + 5 + 6 = 21).
Si el material exhibe simetría en su respuesta elástica, el número de elementos independientes en la\(S\) matriz se puede reducir aún más. En el caso más sencillo de un material isotrópico, cuyas rigideces son las mismas en todas las direcciones, sólo dos elementos son independientes. Anteriormente hemos demostrado que en dos dimensiones las relaciones entre deformaciones y tensiones en materiales isotrópicos pueden escribirse como
\[\begin{array} {c} {\epsilon_x = \dfrac{1}{E} (\sigma_x - \nu \sigma_y)} \\ {\epsilon_y = \dfrac{1}{E} (\sigma_y - \nu \sigma_x)} \\ {\gamma_{xy} = \dfrac{1}{G} \tau_{xy}} \end{array}\]
junto con la relación
\[G = \dfrac{E}{2(1 + \nu)}\nonumber\]
Extendiendo esto a tres dimensiones, la forma pseudovector-matriz de la Ecuación 3.4.1 para los mates isotrópicos es
\[\left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right \} = \begin{bmatrix} \tfrac{1}{E} & \tfrac{-\nu}{E} & \tfrac{-\nu}{E} & 0 & 0 & 0 \\ \tfrac{-\nu}{E} & \tfrac{1}{E} & \tfrac{-\nu}{E} & 0 & 0 & 0 \\ \tfrac{-\nu}{E} & \tfrac{-\nu}{E} & \tfrac{1}{E} & 0 & 0 & 0 \\ 0 & 0 & 0 & \tfrac{1}{G} & 0 & 0 \\ 0 & 0 & 0 & 0 & \tfrac{1}{G} & 0 \\ 0 & 0 & 0 & 0& 0 & \tfrac{1}{G} \end{bmatrix} \left \{ \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \tau_{yz} \\ \tau_{xz} \\ \tau_{xy} \end{matrix} \right \}\]
La cantidad entre paréntesis se llama la matriz de cumplimiento del material, denotada\(S\) o\(S_{ij}\). Es importante captar el significado físico de sus diversos términos. Directamente a partir de las reglas de multiplicación matricial, el elemento en la\(i^{th}\) fila y\(j^{th}\) columna de\(S_{ij}\) es la contribución de la\(j^{th}\) tensión a la\(i^{th}\) deformación. Por ejemplo, el componente en la posición 1,2 es la contribución de la tensión\(y\) -direction a la deformación\(x\) -direction: multiplicar\(\sigma_y\) por\(1/E\) da la deformación\(y\) -direction generada por\(\sigma_y\), y luego multiplicar esta por\(-\nu\) da la cepa de Poisson inducidos en la\(x\) dirección. Los elementos cero muestran la falta de acoplamiento entre los componentes normal y cortante.
La ley constitutiva isotrópica también se puede escribir usando notación índice como (ver Ejercicio\(\PageIndex{1}\))
\[\epsilon_{ij} = \dfrac{1 + \nu}{E} \sigma_{ij} - \dfrac{\nu}{E} \delta_{ij} \sigma_{kk}\]
donde aquí se usa la forma indicial de cepa y\(G\) ha sido eliminada usando\(G = E/2(1 + \nu)\) El símbolo\(\delta_{ij}\) es el delta Kroenecker, descrito en el Módulo sobre Notación Matriz e Índice.
Si queremos escribir las tensiones en términos de las cepas, la Eqn 3.4.3 puede invertirse. En casos de tensión plana (\(\sigma_z = \tau_{xz} = \tau_{yz} = 0\)), esto rinde
\[\left \{ \begin{matrix} \sigma_x \\ \sigma_y \\ \tau_{xy} \end{matrix} \right \} = \dfrac{E}{1-\nu^2} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & (1 - \nu)/2 \end{bmatrix} \left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \gamma_{xy} \end{matrix} \right \}\]
donde nuevamente\(G\) ha sido sustituido por\(E/2(1 + \nu)\). O bien, en notación abreviada:
\[\sigma = D \epsilon\]
donde\(D = S^{-1}\) está la matriz de rigidez.
Componentes hidrostáticos y distorsionantes
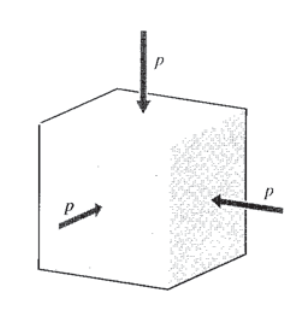
Un estado de compresión hidrostática, representado en la Figura 1, es aquel en el que no existen esfuerzos cortantes y donde todas las tensiones normales son iguales a la presión hidrostática:
\[\sigma_x = \sigma_y = \sigma_z = -p\nonumber\]
donde el signo menos indica que la compresión es convencionalmente positiva para la presión pero negativa para la tensión. Para este estado de estrés obviamente es cierto que
\[\dfrac{1}{3} (\sigma_x + \sigma_y + \sigma_z) = \dfrac{1}{3} \sigma_{kk} = -p\nonumber\]
de manera que la presión hidrostática es la tensión normal media negativa. Esta cantidad es apenas un tercio de la tensión invariante\(I_1\), que es un reflejo de la presión hidrostática siendo la misma en todas las direcciones, no variando con las rotaciones de los ejes.
En muchos casos, además de la compresión hidrostática directa, sigue siendo conveniente “disociar” el componente hidrostático (o “dilatacional”) del tensor de tensión:
\[\sigma_{ij} = \dfrac{1}{3} \sigma_{kk} \delta_{ij} + \sum_{ij}\]
Aquí\(\sum_{ij}\) está lo que queda de\(\sigma_{ij}\) después de restar el componente hidrostático. Se puede mostrar que el\(\sum_{ij}\) tensor representa un estado de cizallamiento puro, es decir, existe una transformación del eje tal que todas las tensiones normales desaparecen (ver Ejercicio\(\PageIndex{5}\)). El\(\sum_{ij}\) se llama el componente distorsionante, o desviatorio, de la tensión. Por lo tanto, todos los estados de estrés pueden considerarse como que tienen dos componentes como se muestra en la Figura 2, uno puramente extensivo y otro puramente distorcional. Este concepto es conveniente porque el material responde a estos componentes de tensión es de maneras muy diferentes. Por ejemplo, el flujo plástico y viscoso es impulsado predominantemente por componentes distorsionantes, con el componente hidrostático causando solo deformación elástica.

Ejemplo\(\PageIndex{1}\)
Considerar el estado de estrés
\[\sigma = \begin{bmatrix} 5 & 6 & 7 \\ 6 & 8 & 9 \\ 7 & 9 & 2 \end{bmatrix}, \text{ GPa} \nonumber\]
El estrés normal medio es\(\sigma_{kk}/3 = (5 + 8 + 2)/3 = 5\), por lo que la descomposición del estrés es
\[\sigma = \dfrac{1}{3} \sigma_{kk} \delta_{ij} + \sum_{ij} = \begin{bmatrix} 5 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 5 \end{bmatrix} + \begin{bmatrix} 0 & 6 & 7 \\ 6 & 3 & 9 \\ 7 & 9 & -3 \end{bmatrix}\nonumber\]
No es obvio que el componente desviatorio dado en la segunda matriz representa cizallamiento puro, ya que hay componentes distintos de cero en su diagonal. Sin embargo, una transformación de tensión usando ángulos de Euler\(\psi = \phi = 0, \theta = -9.22^{\circ}\) da el estado de tensión
\[\sum' = \begin{bmatrix} 0.00 & 4.80 & 7.87 \\ 4.80 & 0.00 & 9.49 \\ 7.87 & 9.49 & 0.00 \end{bmatrix}\nonumber\]
El componente hidrostático de la tensión está relacionado con la deformación volumétrica a través del módulo de compresibilidad (\(-p = K \Delta V/V\)), por lo que
\[\dfrac{1}{3} \sigma_{kk} = K\epsilon_{kk}\]
De manera similar al estrés, la cepa también se puede disociar como
\[\epsilon_{ij} = \dfrac{1}{3} \epsilon_{kk} \delta_{ij} + e_{ij}\nonumber\]
donde\(e_{ij}\) es el componente desviatorio de la cepa. Los componentes desviatorios de tensión y deformación están relacionados por el módulo de cizallamiento del material:
\[\sum_{ij} = 2Ge_{ij}\]
donde se necesita el factor 2 porque las descripciones tensoras de la cepa son la mitad de las cepas clásicas para las que se\(G\) han tabulado los valores de. Escribir las ecuaciones constitutivas en forma de Eqns. 3.4.8 y 3.4.9 produce una forma simple sin los términos de acoplamiento en la\(E-\nu\) forma convencional.
Ejemplo\(\PageIndex{2}\)
Usando el estado de tensión del ejemplo anterior junto con las constantes elásticas para el acero (\(E = 207\)GPa,\(K = E/3(1 - 2\nu) = 173\) GPa\(\nu = 0.3\),\(G = E/2(1 + \nu) = 79.6\) GPa), los componentes dilatacionales y distorsionantes de la deformación son
\[\delta_{ij} \epsilon_{kk} = \dfrac{\delta_{ij} \sigma_kk}{3K} = \begin{bmatrix} 0.0289 & 0 & 0 \\ 0 & 0.0289 & 0 \\ 0 & 0 & 0.0289 \end{bmatrix}\nonumber\]
\[e_{ij} = \dfrac{\sum_{ij}}{2G} = \begin{bmatrix} 0 & 0.0378 & 0.0441 \\ 0.0378 & 0.0189 & 0.0567 \\ 0.0441 & 0.0567 & -0.0189 \end{bmatrix}\nonumber\]
La cepa total es entonces
\[\epsilon_{ij} = \dfrac{1}{3} \epsilon_{kk} \delta_{ij} + e_{ij} = \begin{bmatrix} 0.00960 & 0.0378 & 0.0441 \\ 0.0378 & 0.0285 & 0.0567 \\ 0.0441 & 0.0567 & -0.00930 \end{bmatrix}\nonumber\]
Si evaluamos la cepa total usando la Ecuación 3.4.4, tenemos
\ (\ épsilon_ {ij} =\ dfrac {1 +\ nu} {E}\ sigma_ij -\ dfrac {\ nu} {E}\ delta_ {ij}\ sigma_ {kk} =\ begin {bmatrix} 0.00965 & 0.0377 & 0.0440\\ 0.0377 & 0.0285 & 0.0565\\ 0.0440 y 0.0565 & -0.00915\ fin {bmatrix}\ nonumber\]
Estos resultados son los mismos, difiriendo solo por error de redondeo.
Modelo de deformación finita
Cuando las deformaciones se hacen grandes, pueden surgir no linealidades tanto geométricas como materiales que son importantes en muchos problemas prácticos. En estos casos, el analista debe emplear no solo una medida de deformación diferente, como la cepa Lagrangiana descrita en el Módulo 8, sino también diferentes medidas de tensión (la “segunda tensión Piola-Kirchoff” reemplaza la tensión de Cauchy cuando se usa la cepa lagrangiana) y diferentes leyes constitutivas de tensión-deformación también. Un tratamiento de estas formulaciones está más allá del alcance de estos módulos, pero aquí se describirá un modelo simple de tensión-deformación no lineal para materiales gomosos para ilustrar algunos aspectos del análisis de deformación finita. El texto de Bathe (K.-J. Bathe, Finite Element Procedures in Engineering Analysis, Prentice-Hall, 1982.) proporciona una discusión más extensa de esta área, incluyendo implementaciones de elementos finitos.
En el caso de pequeños desplazamientos, la tensión\(\epsilon_x\) viene dada por la expresión:
\[\epsilon_x = \dfrac{1}{E} [\sigma_x - \nu (\sigma_y + \sigma_z)]\nonumber\]
Para el caso de los elastómeros con\(\nu = 0.5\), esto se puede reescribir en términos de la tensión media\(\sigma_m = (\sigma_x + \sigma_y + \sigma_z)/3\) como:
\[2 \epsilon_x = \dfrac{3}{E} (\sigma_x - \sigma_m)\nonumber\]
Para el caso de gran deformación, se ha propuesto la siguiente relación análoga-tensión:
\[\lambda_x^2 = 1 + 2 \epsilon_x = \dfrac{3}{E} (\sigma_x - \sigma_m^*)\]
donde aquí\(\epsilon_x\) está la cepa Lagrangiana y\(\sigma_m^*\) es un parámetro no necesariamente igual a\(\sigma_m\). El\(\sigma_m^*\) parámetro se puede encontrar para el caso de tensión uniaxial considerando las contracciones transversales\(\lambda_y = \lambda_z\):
\[\lambda_y^2 = \dfrac{3}{E} (\sigma_y - \sigma_m^*)\nonumber\]
Ya que para el caucho\(\lambda_x \lambda_y \lambda_z = 1\),\(\lambda_y^2 = 1/\lambda_x\). Haciendo esta sustitución y resolviendo\(\sigma_m^*\):
\[\sigma_m^* = \dfrac{-E\lambda_y^2}{3} = \dfrac{-E}{3\lambda_x}\nonumber\]
Sustituyendo esto de nuevo en la Ecuación 3.4.10,
\[\lambda_x^2 = \dfrac{E}{3} (\sigma_x - \dfrac{E}{3\lambda_x})\nonumber\]
Resolviendo para\(\sigma_x\),
\[\sigma_x = \dfrac{E}{3} (\lambda_x^2 - \dfrac{1}{\lambda_x})\nonumber\]
Aquí el estrés\(\sigma_x = F/A\) es el estrés “verdadero” basado en el área transversal real (contraída). El estrés de “ingeniería”\(\sigma_e = F/A_0\) basado en el área original\(A_0 = A \lambda_x\) es:
\[\sigma_e = \dfrac{\sigma_x}{\lambda_x} = G\left (\lambda_x - \dfrac{1}{\lambda_x^2} \right )\nonumber\]
donde\(G = E/2(1 + \nu) = E/3\) para\(\nu = 1/2\). Este resultado es el mismo que el obtenido en el Módulo 2 al considerar la fuerza derivada de la entropía reducida a medida que se extienden los segmentos moleculares que abarcan sitios de entrecruzamiento. Aparece aquí a partir de una hipótesis simple de respuesta tensión-deformación, utilizando una medida adecuada de deformación finita.
Materiales anisotrópicos

Si el material tiene una textura como madera o compuestos de fibra reforzados unidireccionalmente como se muestra en la Figura 3, el módulo\(E_1\) en la dirección de la fibra será típicamente mayor que aquellos en las direcciones transversales (\(E_2\)y\(E_3\)). Cuando\(E_1 \ne E_2 \ne E_3\), se dice que el material es ortotrópico. Es común, sin embargo, que las propiedades en el plano transversal a la dirección de la fibra sean isotrópicas a una buena aproximación\((E_2 = E_3)\); dicho material se denomina transversalmente isotrópico. Las leyes constitutivas elásticas deben ser modificadas para dar cuenta de esta anisotropía, y la siguiente forma es una extensión de la Ecuación 3.4.3 para materiales isotrópicos transversalmente:
\[\left \{ \begin{matrix} \epsilon_1 & \epsilon_2 & \gamma_{12} \end{matrix} \right \} = \begin{bmatrix} 1/E_1 & -\nu_{21}/E_2 & 0 \\ -\nu_{12}/E_1 & 1/E_2 & 0 \\ 0 & 0 & 1/G_{12} \end{bmatrix} \left \{ \begin{matrix} \sigma_1 & \sigma_2 & \tau_{12} \end{matrix} \right \}\]
El parámetro\(\nu_{12}\) es la relación principal de Poisson; es la relación de la deformación inducida en la dirección 2 por una deformación aplicada en la dirección 1. Este parámetro no se limita a valores menores a 0.5 como en materiales isotrópicos. Por el contrario,\(\nu_{21}\) da la tensión inducida en la dirección 1 por una deformación aplicada en la dirección 2. Dado que la dirección 2 (transversal a las fibras) suele tener mucha menos rigidez que la dirección 1, debería quedar claro que una deformación dada en la dirección 1 generalmente desarrollará una deformación mucho mayor en la dirección 2 que la misma deformación en la dirección 2 inducirá una deformación en la dirección 1. De ahí que por lo general tendremos\(\nu_{12} > \nu_{21}\). Hay cinco constantes en la ecuación anterior (\(E_1, E_2, \nu_{12}, \nu_{21}\)y\(G_{12}\)). Sin embargo, sólo cuatro de ellos son independientes; ya que la\(S\) matriz es simétrica,\(\nu_{21}/E2 = \nu_{12}/E1\).
Una tabla de constantes elásticas y otras propiedades para materiales anisotrópicos ampliamente utilizados se puede encontrar en el Módulo sobre Propiedades de Capa Compuesta.
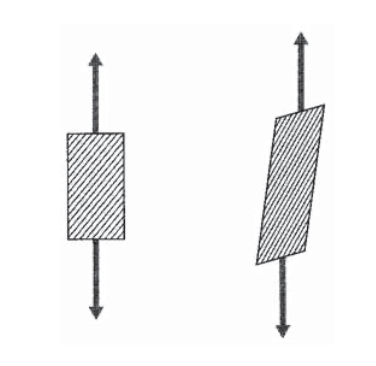
La forma simple de la Ecuación 3.4.11, con ceros en los términos que representan el acoplamiento entre componentes normales y cortantes, se obtiene solo cuando los ejes están alineados a lo largo de las direcciones principales del material; es decir, a lo largo y transversal a los ejes de las fibras. Si los ejes están orientados a lo largo de alguna otra dirección, se poblarán todos los términos de la matriz de cumplimiento, y la simetría del material no será evidente. Si por ejemplo la dirección de la fibra está fuera del eje de la dirección de carga, el material desarrollará deformación por cizallamiento a medida que las fibras intentan orientarse a lo largo de la dirección de carga como se muestra en la Figura 4 Por lo tanto, habrá un acoplamiento entre una tensión normal y una deformación por cizallamiento, que nunca ocurre en un material isotrópico.
La ley de transformación para el cumplimiento se puede desarrollar a partir de las leyes de transformación para tensiones y tensiones, utilizando los procedimientos descritos en el Módulo 10 (Transformaciones). Por transformaciones sucesivas, la forma pseudovector para deformación en una\(x-y\) dirección arbitraria mostrada en la Figura 5 se relaciona con la deformación en las direcciones 1-2 (material principal), luego con las tensiones en las direcciones 1-2, y finalmente con las tensiones en las\(x-y\) direcciones. La agrupación final de matrices de transformación que relacionan las\(x-y\) deformaciones con las\(x-y\) tensiones es entonces la matriz de conformidad transformada en la\(x-y\) dirección:
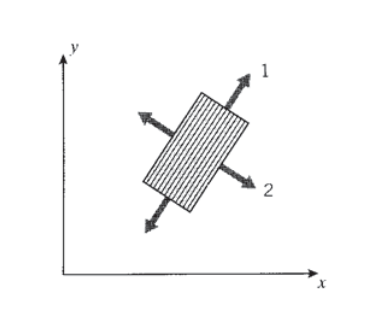
\[\left \{ \begin{matrix} \epsilon_x & \epsilon_y & \gamma_{xy} \end{matrix} \right \} = R \left \{ \begin{matrix} \epsilon_x & \epsilon_y & \tfrac{1}{2} \gamma_{xy} \end{matrix} \right \} = RA^{-1} \left \{ \begin{matrix} \epsilon_1 & \epsilon_2 & \tfrac{1}{2} \gamma_{12} \end{matrix} \right \} = RA^{-1}R^{-1} \left \{ \begin{matrix} \epsilon_1 & \epsilon_2 & \gamma_{12} \end{matrix} \right \}\nonumber\]
\[=RA^{-1}R^{-1} S \left \{ \begin{matrix} \sigma_1 & \sigma_2 & \tau_{12} \end{matrix} \right \} = RA^{-1}RSA \left \{ \begin{matrix} \sigma_x & \sigma_y & \sigma_{xy} \end{matrix} \right \} = \bar{S} \left \{ \begin{matrix} \sigma_x & \sigma_y & \sigma_{xy} \end{matrix} \right \}\nonumber\]
donde\(\bar{S}\) está la matriz de cumplimiento transformada relativa a\(x-y\) los ejes. Aquí\(A\) está la matriz de transformación, y\(R\) es la matriz de Reuter definida en el Módulo sobre Transformaciones de Tensor. La inversa de\(\bar{S}\) es\(\bar{D}\), la matriz de rigidez relativa a\(x-y\) los ejes:
\[\bar{S} = RA^{-1}SA, \ \ \bar{D} = \bar{S}^{-1}\]
Ejemplo\(\PageIndex{1}\)
Considere una capa de compuesto Kevlar-epoxi con una rigidez\(E_1 = 82, E_2 = 4, G_{12} = 2.8\) (todos GPa) y\(\nu_{12} = 0.25\). La matriz de cumplimiento\(S\) en la dirección 1-2 (material) es:
\[S = \begin{bmatrix} 1/E_1 & -\nu_{21} /E_2 & 0 \\ -\nu_{12} /E_1 & 1/E_2 & 0 \\ 0 & 0 & 1/G_{12} \end{bmatrix} = \begin{bmatrix} .1220 \times 10^{-10} & -.3050 \times 10^{-11} & 0 \\ -.3050 \times 10^{-11} & .2500 \times 10^{-9} & 0 \\ 0 & 0 & .3571 \times 10^{-9} \end{bmatrix}\nonumber\]
Si la capa está orientada con la dirección de la fibra (la dirección “1")\(\theta = 30^{\circ}\) desde los\(x-y\) ejes, la matriz de transformación apropiada es
\[A = \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} = \begin{bmatrix} .7500 & .2500 & .8660 \\ .2500 & .7500 & -.8600 \\ -.4330 & .4330 & .5000 \end{bmatrix}\nonumber\]
La matriz de conformidad relativa a los\(x-y\) ejes es entonces
\[\bar{S} = RA^{-1}R^{-1}SA = \begin{bmatrix} .8830 \times 10^{-10} & -.1970 \times 10^{-10} & -1.222 \times 10^{-9} \\ -.1971 \times 10^{-10} & .2072 \times 10^{-9} & -.8371 \times 10^{-10} \\ 1.222 \times 10^{-9} & -.8369 \times 10^{-10} & -2905 \times 10^{-9} \end{bmatrix}\nonumber\]
Tenga en cuenta que esta matriz es simétrica (hasta dentro del error de redondeo numérico), pero que existen valores de acoplamiento distintos de cero. Un usuario no consciente de la composición interna del material lo consideraría completamente anisotrópico.
Las constantes de ingeniería aparentes que se observarían si la capa se ensayara en las direcciones en\(x-y\) lugar de 1-2 se pueden encontrar directamente a partir de la\(\bar{S}\) matriz trasnformada. Por ejemplo, el módulo elástico aparente en la\(x\) dirección es\(E_x = 1/\bar{S}_{1,1} = 1/(.8830 \times 10^{-10} = 11.33\) GPa.
Ejercicio\(\PageIndex{1}\)
Ampliar las formas indiciales de las ecuaciones gobernantes para la elasticidad sólida en tres dimensiones:
\[\text{equilibrium: } \sigma_{ij,j} = 0\nonumber\]
\[\text{kinematric: } \epsilon_{ij} = (u_{i,j} + u_{j, i})/2\nonumber\]
\[\text{constitutive: } \epsilon_{ij} = \dfrac{1 + \nu}{E} \sigma_{ij} - \dfrac{\nu}{E} \delta_{ij} \sigma_{kk} + \alpha \delta_{ij} \Delta T\nonumber\]
donde\(\alpha\) es el coeficiente de expansión térmica lineal y\(\Delta T\) es un cambio de temperatura.
Ejercicio\(\PageIndex{2}\)
(a) Redactar la matriz\(S\) de cumplimiento de la Ecuación 3.4.3 para policarbonato utilizando los datos del Módulo sobre Propiedades del Material.
b) Utilizar inversión matricial para obtener la matriz de rigidez\(D\).
c) Utilizar la multiplicación matricial para obtener las tensiones necesarias para inducir las cepas
\[\epsilon = \left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right \} = \left \{ \begin{matrix} 0.02 \\ 0.0 \\ 0.03 \\ 0.01 \\ 0.025 \\ 0.0 \end{matrix} \right \}\nonumber\]
Ejercicio\(\PageIndex{3}\)
(a) Escriba la matriz\(S\) de cumplimiento de la Ecuación 3.4.3 para una aleación de aluminio utilizando los datos del Módulo sobre Propiedades del Material.
(b) Utilizar inversión matricial para obtar la matriz de rigidez\(D\).
c) Utilizar la multiplicación matricial para obtener las tensiones necesarias para inducir las cepas
\[\epsilon = \left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right \} = \left \{ \begin{matrix} 0.01 \\ 0.02 \\ 0.0 \\ 0.0 \\ 0.15 \\ 0.0 \end{matrix} \right \}\nonumber\]
Ejercicio\(\PageIndex{4}\)
Dado el tensor de estrés
\[\sigma_{ij} = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 7 \end{bmatrix} \ \ \text{(MPa)}\nonumber\]
(a) Disociar\(\sigma_{ij}\) en partes desviatorias y dilatacionales\(\sum_{ij}\) y\((1/3) \sigma_{kk} \delta_{ij}\).
(b) Dados\(G = 357\) MPa y\(K = 1.67\) GPa, obtener los tensores de deformación desviatoria y dilatacional\(e_{ij}\) y\((1/3)\epsilon_{kk} \delta_{ij}\).
(c) Agregar los componentes de deformación desviatoria y dilatacional obtenidos anteriormente para obtener el tensor de deformación total\(\epsilon_{ij}\).
d) Calcular el tensor de deformación\(\epsilon_{ij}\) utilizando la forma alternativa de la ley constitutiva elástica para sólidos elásticos isotrópicos:
\[\epsilon_{ij} = \dfrac{1 + \nu}{E} \sigma_{ij} - \dfrac{\nu}{E} \delta_{ij} \sigma_{kk}\nonumber\]
Comparar el resultado con el obtenido en (c).
Ejercicio\(\PageIndex{5}\)
Proporcionar un argumento de que cualquier matriz de tensión que tenga una traza cero puede transformarse en una que tenga solo ceros en su diagonal; es decir, el tensor de tensión desviatoria\(\sum_{ij}\) representa un estado de cizallamiento puro.
Ejercicio\(\PageIndex{6}\)
Escriba la matriz de cumplimiento\(x-y\) bidimensional\(\bar{S}\) y la matriz de rigidez\(\bar{D}\) (Ecuación 3.4.12) para una sola capa de compuesto de grafito/epoxi con sus fibras alineadas a lo largo de los\(x\) ejes.
Ejercicio\(\PageIndex{7}\)
Escriba la matriz de cumplimiento\(x-y\) bidimensional\(\bar{S}\) y la matriz de rigidez\(\bar{D}\) (Ecuación 3.4.12) para una sola capa de compuesto de grafito/epoxi con sus fibras alineadas 30\(^{\circ}\) del\(x\) eje.


