4.3: Desplazamientos de haz

Introducción

Queremos poder predecir la deflexión de las vigas en flexión, porque muchas aplicaciones tienen limitaciones en la cantidad de deflexión que se puede tolerar. Otra necesidad común de análisis de deflexión surge de las pruebas de materiales, en las que se mide la deflexión transversal inducida por una carga de flexión. Si conocemos la relación esperada entre la carga y la deflexión, podemos “retroceder” las propiedades del material (específicamente el módulo) de la medición. Mostraremos, por ejemplo, que la deflexión en el punto medio de una viga sometida a “flexión de tres puntos” (viga cargada en su centro y simplemente soportada en sus bordes) es

\(\delta_P = \dfrac{PL^3}{48EI}\)

donde la longitud\(L\) y el momento de inercia\(I\) son parámetros geométricos. Si la relación de\(\delta_P\) a\(P\) se mide experimentalmente, se\(E\) puede determinar el módulo. Una rigidez medida de esta manera se llama el módulo de flexión.

Hay una serie de enfoques para el problema de la desviación del haz, y muchos textos gastan una buena cantidad de impresiones sobre este tema. El siguiente tratamiento describe solo algunos de los métodos más sencillos, más con el objetivo de comprender los conceptos generales que con desarrollar mucha facilidad para hacerlos manualmente. En la práctica, los ingenieros de diseño suelen consultar tabulaciones de manual de fórmulas de deflexión según sea necesario, por lo que incluso antes de la era de la informática muchos de estos métodos eran un poco académicos.

Integración múltiple

En el Módulo 12, vimos cómo dos integraciones de la función de carga\(q(x)\) producen primero la función de cizallamiento\(V(x)\) y luego la función de momento\(M(x)\):

\[V = - \int q(x) dx + c_1\]

\[M = - \int V(x) dx + c_2\]

donde las constantes de integración\(c_1\) y\(c_2\) se evalúan a partir de condiciones de límite adecuadas en\(V\) y\(M\). (Si se utilizan funciones de singularidad, las condiciones de contorno se incluyen explícitamente y las constantes de integración\(c_1\) y\(c_2\) son idénticamente cero). De la Ecuación 6 en el Módulo 13, la curvatura\(v_{,xx} (x)\) es justo el momento dividido por el módulo de sección\(EI\). Otras dos integraciones luego dan

\[v_{,x} (x) = \dfrac{1}{EI} \int M(x) dx + c_3\]

\[v(x) = \int v_{,x} (x) + c_4\]

donde\(c_3\) y\(c_4\) se determinan a partir de las condiciones de contorno en pendiente o deflexión.

Ejemplo\(\PageIndex{1}\)

Figura 1: Flexión de tres puntos.

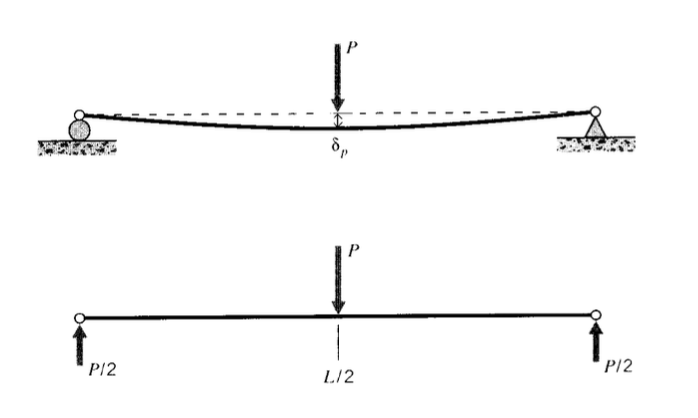
Como ilustración de este proceso, considere el caso de la “flexión de tres puntos” que se muestra en la Figura 1. Esta geometría se utiliza a menudo en las pruebas de materiales, ya que evita la necesidad de sujetar la muestra al aparato de prueba. Si la carga\(P\) se aplica en el punto medio, las fuerzas de reacción en\(A\) y\(B\) son iguales a la mitad de la carga aplicada. La función de carga es entonces

Integrando de acuerdo con el esquema anterior:

\[\begin{array} {c} {V(x) = - \dfrac{P}{2} \langle x \rangle^0 + P \langle x - \dfrac{L}{2} \rangle^0} \\ {M(x) = \dfrac{P}{2} \langle x \rangle^1 - P \langle x - \dfrac{L}{2} \rangle^1} \\ {EIv_{,x} (x) = \dfrac{P}{4} \langle x \rangle^2 - \dfrac{P}{2} \langle x - \dfrac{L}{2} \rangle^2 + c_3} \end{array}\]

A partir de la simetría, la viga tiene pendiente cero en el punto medio. De ahí\(v_{,x} = 0 @ x = L/2\), así se\(c_3\) puede encontrar que lo es\(-PL^2/16\). Integrando de nuevo:

La deflexión es cero en el extremo izquierdo, entonces\(c_4 = 0\). Reordenando, la deflexión del haz viene dada por

\[v = \dfrac{P}{48EI} [4x^3 - 3L^2x - 8 \langle x - \dfrac{L}{2} \rangle^3]\]

La desviación máxima ocurre en\(x = L/2\), que podemos evaluar justo antes del término de singularidad

\[\delta_{\max} = \dfrac{PL^3}{48EI}\]

Esta expresión es muy utilizada en las pruebas de flexión, y es el ejemplo utilizado para comenzar este módulo.

Antes de que se\(q(x)\) pueda escribir la función de carga, se deben determinar las fuerzas de reacción en los soportes de la viga. Si el haz está determinado estáticamente, como en el ejemplo anterior, esto se puede hacer invocando las ecuaciones de equilibrio estático. La determinación estática significa que solo dos fuerzas de reacción o momentos pueden estar presentes, ya que solo tenemos un equilibrio de fuerzas en la dirección transversal al eje de la viga y una ecuación de momento disponible. Una viga simplemente soportada (una que descansa sobre solo dos soportes) o una viga simplemente en voladizo son ejemplos de tales vigas determinadas; en el primer caso hay una fuerza de reacción en cada soporte, y en el último caso hay una fuerza transversal y un momento en el extremo sujeto.

Por supuesto, no hay ninguna razón de ingeniería estricta para limitar el número de soportes de viga a aquellos suficientes para el equilibrio estático. Agregar soportes “adicionales” limitará las deformaciones y tensiones, y esto a menudo valdrá la pena a pesar del gasto adicional de construcción. Pero el análisis es ahora un poco más complicado, ya que no todas las reacciones desconocidas se pueden encontrar a partir de las ecuaciones de equilibrio estático. En estos casos estáticamente indeterminados será necesario invocar restricciones geométricas para desarrollar suficientes ecuaciones para resolver el problema.

Esto se hace escribiendo las ecuaciones de pendiente y deflexión, llevando las fuerzas y momentos de reacción desconocidos como parámetros indeterminados. Las pendientes y deflexiones se fijan entonces a sus valores conocidos en los soportes, y las ecuaciones resultantes se resuelven para las incógnitas. Si por ejemplo una viga descansa sobre tres soportes, habrá tres fuerzas de reacción desconocidas, y necesitaremos un total de cinco ecuaciones: tres para las fuerzas desconocidas y dos más para las constantes de integración que surgen cuando se escriben las ecuaciones de pendiente y deflexión. Dos de estas ecuaciones están dadas por equilibrio estático, y tres más se obtienen estableciendo las deflexiones en los soportes a cero. El siguiente ejemplo ilustra el procedimiento, que es sencillo aunque tedioso si se realiza manualmente.

Ejemplo\(\PageIndex{2}\)

Considere una viga de triple soporte de longitud\(L = 15\) como se muestra en la Figura 2, que lleva una carga uniforme constante de\(w = -10\). No hay suficientes ecuaciones de equilibrio para determinar las fuerzas de reacción, y\(R_a\)\(R_b\), por lo tanto\(R_c\), estas se dejan como incógnitas mientras que la integración múltiple se usa para desarrollar una ecuación de deflexión:

Figura 2: Viga de carga uniforme que descansa sobre tres soportes.

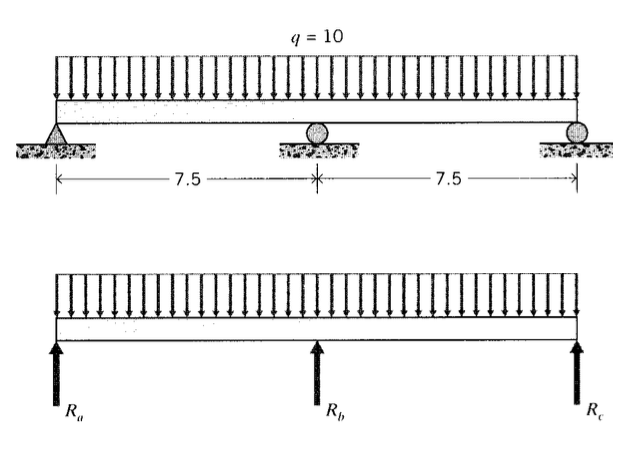
Estas ecuaciones tienen 5 incógnitas:\(R_a, R_b, R_c, c_1\), y\(c_2\). Estos deben obtenerse a partir de las dos ecuaciones de equilibrio

y los tres desplazamientos cero conocidos en los soportes

\(y(0) = y(L/2) = y(L) = 0\)

Aunque el proceso es sencillo, hay mucho álgebra por recorrer. Los haces estáticamente indeterminados tienden a generar tediosas matemáticas, pero afortunadamente esto se puede reducir en gran medida con el software moderno. Siga la facilidad con la que este ejemplo es manejado por el paquete Maple V (algunas de las respuestas de Maple eliminadas por brevedad):

> # read the library containing the Heaviside function
> readlib(Heaviside);
> # use the Heaviside function to define singularity functions;
> # sfn(x,a,n) is same is <x-a>^n
> sfn := proc(x,a,n) (x-a)^n * Heaviside(x-a) end; 
> # define the deflection function:
> y := (x)-> (Ra/6)*sfn(x,0,3)+(Rb/6)*sfn(x,7.5,3)+(Rc/6)*sfn(x,15,3)
>   -(10/24)*sfn(x,0,4)+c1*x+c2;
> # Now define the five constraint equations; first vertical equilibrium:
> eq1 := 0=Ra+Rb+Rc-(10*15);
> # rotational equilibrium:
> eq2 := 0=(10*15*7.5)-Rb*7.5-Rc*15;
> # Now the three zero displacements at the supports:
> eq3 := y(0)=0;
> eq4 := y(7.5)=0;
> eq5 := y(15)=0;
> # set precision; 4 digits is enough:
> Digits:=4;
> # solve the 5 equations for the 5 unknowns:
> solve({eq1,eq2,eq3,eq4,eq5},{Ra,Rb,Rc,c1,c2});
            {c2 = 0, c1 = -87.82, Rb = 93.78, Ra = 28.11, Rc = 28.11} 
> # assign the known values for plotting purposes:
> c1:=-87.82;c2:=0;Ra:=28.11;Rb:=93.78;Rc:=28.11;
> # the equation of the deflection curve is:
> y(x);
            3                                    3
4.686 x Heaviside(x) + 15.63 (x - 7.5) Heaviside(x - 7.5)
                    3                              4
        + 4.686 (x - 15) Heaviside(x - 15) - 5/12 x Heaviside(x) - 87.82 x
> # plot the deflection curve:
> plot(y(x),x=0..15);
> # The maximum deflection occurs at the quarter points: 
> y(15/4);
                                                -164.7 

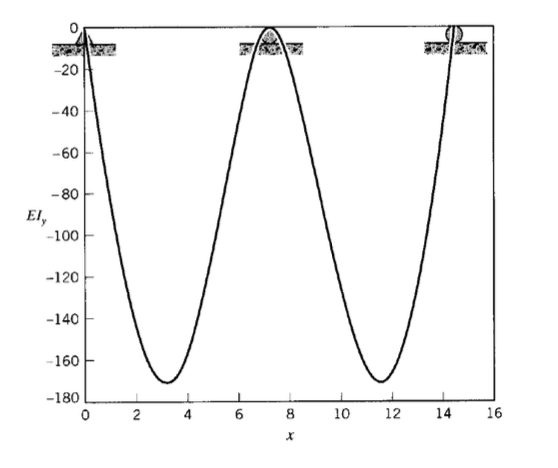
La gráfica de la curva de deflexión se muestra en la Figura 3.

Figura 3: Curva de deflexión\(EIy(x)\) para viga triplicada cargada uniformemente (Note diferencia en escalas horizontales y verticales).

Método de energía

La energía de deformación en la flexión dada por la Ecuación 8 del Módulo 13 se puede usar para encontrar deflexiones, y esto puede ser más conveniente que la integración sucesiva si se desea la deflexión en un solo punto. El teorema de Castigliano da la deflexión congruente a una carga\(P\) como

\(\delta_P = \dfrac{\partial U}{\partial P} = \dfrac{\partial}{\partial P} \int_L \dfrac{M^2 dx}{2EI}\)

Por lo general, es más conveniente hacer la diferenciación antes de la integración, ya que esto disminuye el orden de la expresión en el integrando:

\(\delta P = \int_L \dfrac{M}{EI} \dfrac{\partial M}{\partial P} dx\)

donde aquí\(E\) y\(I\) se supone que no varían con\(x\).

La contribución de cizallamiento a la flexión se puede obtener de manera similar. Conociendo el esfuerzo cortante\(\tau = VQ/Ib\) (omitiendo el\(xy\) subíndice\(\tau\) por ahora), se\(U_s\) puede escribir la energía de deformación debida al cizallamiento

\(U_s = \int_V \dfrac{\tau^2}{2G} dV = \int_L \dfrac{V^2}{2GI} \left [\int_A \dfrac{Q^2}{L^2} dA \right ] dx\)

La integral sobre el área de la sección transversal\(A\) es un factor puramente geométrico, y podemos escribir

\[U_s = \int_L \dfrac{V^2 f_s}{2GA} dA \]

donde el\(f_s\) es un factor de forma adimensional para el cizallamiento definido como

\[f_s = \dfrac{A}{I^2} \int_A \dfrac{Q^2}{b^2} dA\]

Figura 4: Sección de viga rectangular.

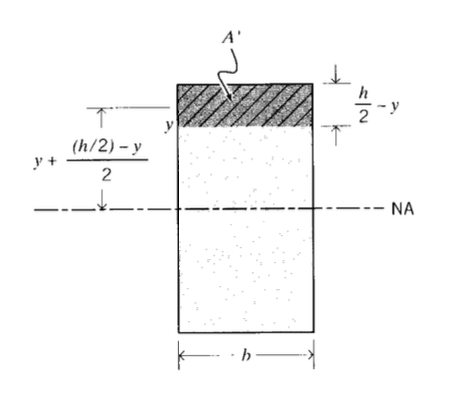
Evaluando\(f_s\) para secciones rectangulares para ilustración (ver Figura 4), tenemos en ese caso

\(A = bh, I = \dfrac{bh^3}{12}\)

\(f_s = \dfrac{(bh)}{(bh^3/12)^2} \int_{-h/2}^{h/2} \dfrac{1}{b^2} Q dy = \dfrac{6}{5}\)

De ahí\(f_s\) que sea lo mismo para todas las secciones rectangulares, independientemente de sus dimensiones particulares. De igual manera, se puede mostrar (ver Ejercicio\(\PageIndex{3}\)) que para secciones circulares sólidas\(f_s\) = 10/9 y para secciones circulares huecas\(f_s\) = 2.

Ejemplo\(\PageIndex{3}\)

Si por ejemplo estamos buscando la deflexión bajo la carga\(P\) en el ejemplo de flexión de tres puntos hecho anteriormente, podemos diferenciar el momento dado en la Ecuación 4.3.5 para obtener

Entonces

Ampliando esto y ajustando los límites de integración para dar cuenta de funciones de singularidad que no han sido activadas:

\(= -\dfrac{PL^3}{48EI}\)

como antes.

La contribución del cizallamiento a la deflexión se puede encontrar usando\(V = P/2\) en la ecuación para energía de deformación. Para el caso de una viga rectangular con\(f_s = 6/5\) tenemos:

\(U_s = \dfrac{(P/2)^2 (6/5)}{2GA}L\)

\(\delta_{P,s} = \dfrac{\partial U_s}{\partial P} = \dfrac{6PL}{20GA}\)

La contribución de cizallamiento se puede comparar con la contribución de flexión reemplazando\(A\) con\(12I/h^2\) (since\(A = bh\) y\(I = bh^3/12\)). Entonces la relación de las contribuciones de cizallamiento a flexión es

\(\dfrac{PLh^2/40GI}{PL^3/24EI} = \dfrac{3h^2 E}{5L^2G}\)

De ahí la importancia de las escalas del término de cizallamiento como (h/L) 2, es decir, cuadráticamente como la relación espacio-profundidad.

El método de energía suele ser conveniente para sistemas que tienen geometrías complicadas y carga combinada. Para ejes delgados que transmiten cargas axiales, torsionales, de flexión y cizallamiento, la energía de deformación es

\[U = \int_L \left (\dfrac{P^2}{2EA} + \dfrac{T^2}{2GJ} + \dfrac{M^2}{2EI} + \dfrac{V^2f_s}{2GA} \right ) dx\]

Ejemplo\(\PageIndex{4}\)

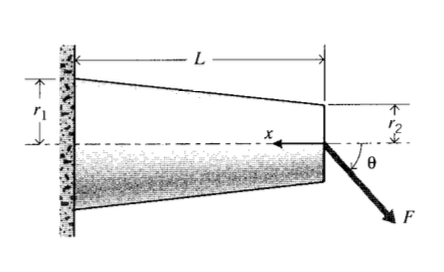
Considere una viga circular en voladizo como se muestra en la Figura 5 que se ahusa desde el radio\(r_1\) hasta\(r_2\) sobre la longitud\(L\). Deseamos determinar la deflexión causada por una fuerza\(F\) aplicada al extremo libre de la viga, en ángulo con respecto\(\theta\) a la horizontal. Volviendo a Maple para evitar el tedio algebraico, los parámetros dimensionales necesarios en la Ecuación 4.3.10 se definen como:

Figura 5: Viga circular cónica.

> r := proc (x) r1 + (r2-r1)*(x/L) end; 
> A := proc (r) Pi*(r(x))^2 end;
> Iz := proc (r) Pi*(r(x))^4 /4 end;
> Jp := proc (r) Pi*(r(x))^4 /2 end; 

donde r (x) es el radio, A (r) es el área de la sección, Iz es el momento rectangular de inercia y Jp es el momento polar de inercia. Las cargas axiales, de flexión y de cizallamiento se dan en términos\(F\) de

> P := F* cos(theta);
> V := F* sin(theta);
> M := proc (x) -F* sin(theta) * x end; 

Las energías de deformación correspondientes a la tensión, flexión y cizallamiento son

> U1 := P^2/(2*E*A(r));
> U2 := (M(x))^2/(2*E*Iz(r));
> U3 := V^2*(10/9)/(2*G*A(r)); 
> U := int( U1+U2+U3, x=0..L); 

Finalmente, la deflexión congruente con la carga\(F\) se obtiene diferenciando la energía de deformación total:

> dF := diff(U,F); 

El resultado de estas manipulaciones rinde

Este desplazamiento es en la dirección de la fuerza aplicada\(F\); las deflexiones horizontal y vertical del extremo de la viga son entonces

\(\delta_x = \delta_F \cos \theta\)

\(\delta_y = \delta_F \sin \theta\)

Superposición

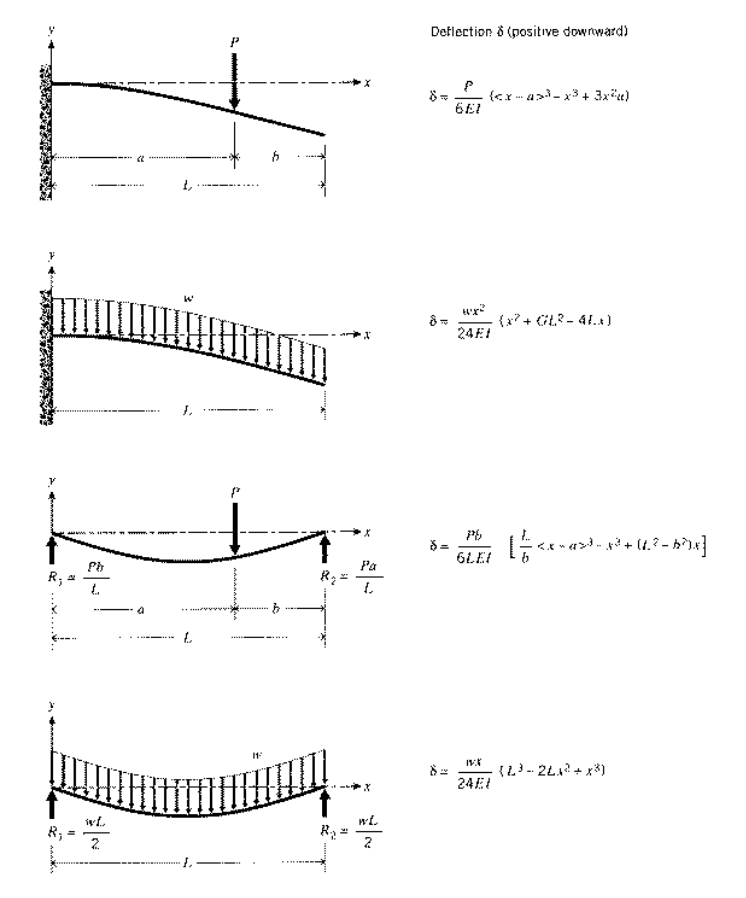
En la práctica, muchas vigas se cargarán de una manera complicada consistente en varias cargas concentradas o distribuidas que actúan en diversas ubicaciones a lo largo de la viga. Aunque estos casos de carga múltiple se pueden resolver desde cero utilizando los métodos descritos anteriormente, a menudo es más fácil resolver el problema superponiendo soluciones de problemas más simples cuyas soluciones se tabulan. La Figura 6 da una colección abreviada de fórmulas de deflexión (Un listado más exhaustivo está disponible en W.C. Young, Roark's Formulas for Stress and Strain, McGraw-Hill, Nueva York, 1989.) que bastará para muchos problemas. El enfoque de superposición es válido ya que las ecuaciones gobernantes son lineales; de ahí que la respuesta a una combinación de cargas sea la suma de las respuestas que serían generadas por cada carga separada actuando sola.

Figura 6: Defecciones para vigas en voladizo y simplemente soportadas, bajo carga concentrada y distribuida.

Ejemplo\(\PageIndex{5}\)

Figura 7: Flexión de cuatro puntos.

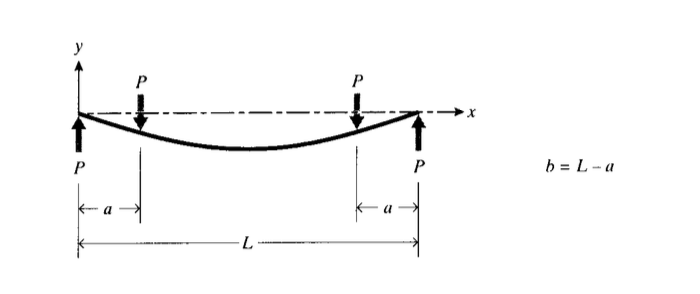
Deseamos encontrar la ecuación de la curva de deflexión para una viga de soporte simple cargada en flexión simétrica de cuatro puntos como se muestra en la Figura 7. De la Figura 6, la deflexión de una viga con una sola carga a una\(a\) distancia del extremo izquierdo es\(\delta (x) = \dfrac{Pb}{6LEI} [\dfrac{L}{b} \langle x - a \rangle^3 - x^3 + (L^2 - b^2) x]\). Nuestro problema actual es que solo dos de esas cargas actúan simultáneamente, así que tenemos

En algunos casos, el diseñador puede no necesitar toda la curva de deflexión, y la superposición de resultados tabulados para la deflexión y pendiente máximas es igualmente válida.

Ejercicio\(\PageIndex{1}\)

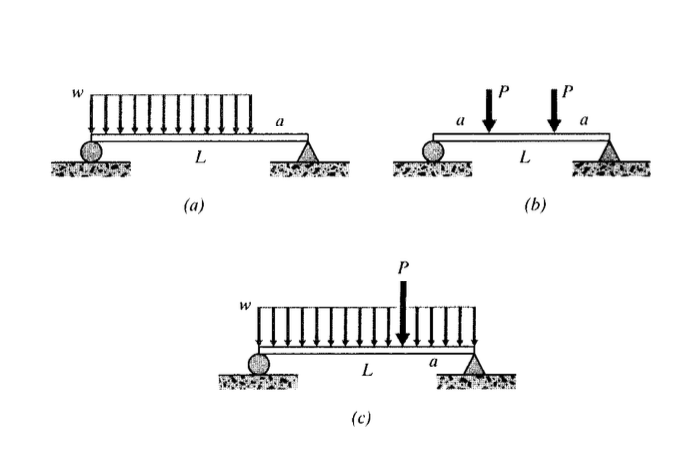
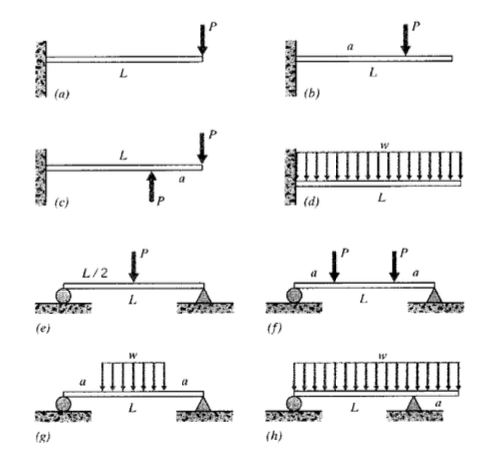
(a) - (h) Escriba expresiones para las curvas de pendiente y deflexión de las vigas que se muestran aquí.

Ejercicio\(\PageIndex{2}\)

(a) - (h) Utilice MapleV (u otro) software para trazar las curvas de pendiente y deflexión para las vigas en Ejercicio\(\PageIndex{1}\), utilizando los valores (según sea necesario)\(L = 25\ in, a = 15\ in, w = 10\ lb/in, P = 150\ lb\).

Ejercicio\(\PageIndex{3}\)

Mostrar que el factor de forma para cizallamiento para una sección transversal circular es

\(f_s = \dfrac{A}{I^2} \int_A \dfrac{Q}{b^2} dA = \dfrac{10}{9}\)

Ejercicio\(\PageIndex{4}\)

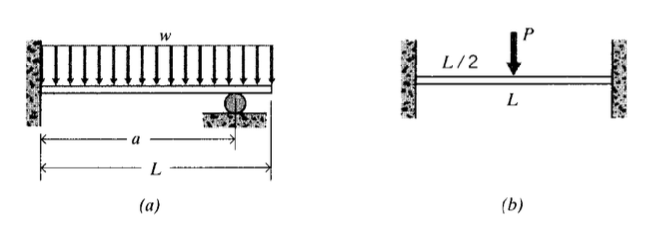
(a) - (b) Determinar las curvas de deflexión para las vigas que se muestran aquí. Trazar estas curvas para los valores (según sea necesario)\(L = 25\ in, a = 5\ in, w = 10\ lb/in, P = 150\ lb\).

Ejercicio\(\PageIndex{5}\)

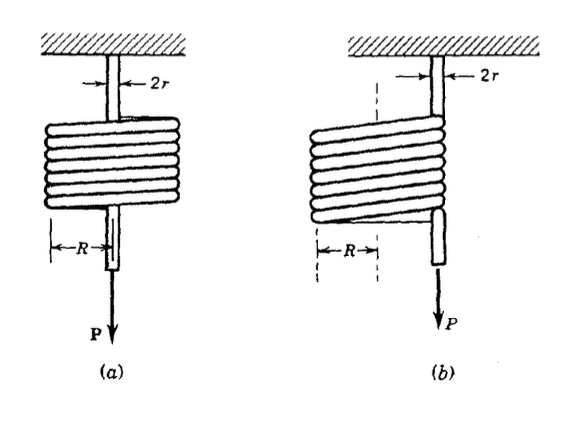
(a) Determinar la deflexión de un muelle en espiral bajo la influencia de una fuerza axial\(F\), incluyendo la contribución de los efectos de flexión, cizallamiento directo y cizallamiento torsional. Usando\(r = 1\ mm\) y\(R = 10\ mm\), computar las magnitudes relativas de las tres contribuciones.

(b) Repita la solución en (a), pero tome la carga axial que se colocará en el radio exterior de la bobina.

Ejercicio\(\PageIndex{6}\)

(a) - (c) Utilice el método de superposición para escribir expresiones para la curva de deflexión\(\delta (x)\) para los casos aquí mostrados.