4.4: Placas compuestas laminadas
- Page ID
- 83295
Introducción
Este documento pretende delinear la mecánica de las placas laminadas reforzadas con fibra, dando lugar a un esquema computacional que relaciona la deformación y curvatura en el plano de un laminado con las tracciones y momentos de flexión que se le imponen. Aunque esta es una pequeña parte del campo general de los compuestos reforzados con fibra, o incluso de la teoría del laminado, es una técnica importante que debe ser entendida por todos los ingenieros de compuestos.
En las secciones siguientes, revisaremos las relaciones constitutivas de materiales isotrópicos en forma de matriz, luego mostraremos que la extensión a láminas compuestas transversalmente isotrópicas es muy sencilla. Dado que cada capa en un laminado puede orientarse arbitrariamente, entonces mostraremos cómo las propiedades elásticas de las láminas individuales se pueden transformar en una dirección común. Finalmente, equilibraremos las tensiones de las capas individuales contra las tracciones aplicadas y los momentos para desarrollar relaciones de gobierno matriciales para el laminado en su conjunto.
Los cálculos para la mecánica de laminados se realizan mejor por computadora, y se describen algoritmos para laminados elásticos, laminados que exhiben efectos de expansión térmica y laminados que exhiben respuesta viscoelástica.
Materiales elásticos lineales isotrópicos
Como se muestra en los textos elementales sobre Mecánica de Materiales (cf. Roylance 1996 (Ver Referencias listadas al final de este documento.)), las cepas cartesianas resultantes de un estado de tensión plana (\(\sigma_z = \tau_{xz} = \tau_{yz} = 0\)) son
\(\gamma_{xy} = \dfrac{1}{G} \tau_{xy}\)
En la tensión plana también hay una deformación en la\(z\) dirección debido al efecto Poisson:\(\epsilon_z = -\nu (\sigma_x + \sigma_y)\); este componente de deformación será ignorado en las secciones a seguir. En las relaciones anteriores hay tres constantes elásticas: el módulo de Young\(E\), la relación\(\nu\) de Poisson y el módulo de cizallamiento\(G\). Sin embargo, para los materiales isotrópicos solo hay dos constantes elásticas independientes y, por ejemplo, se\(G\) pueden obtener de\(E\) y\(\nu\) como
\(G = \dfrac{E}{2(1 + \nu)}\)
Usando la notación matricial, estas relaciones se pueden escribir como
\[\left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_x} \\ {\gamma_{xy}} \end{array} \right \} = \begin{bmatrix} 1/E & -\nu/E & 0 \\ -\nu/E & 1/E & 0 \\ 0 & 0 & 1/G \end{bmatrix} \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\tau_{xy}} \end{array} \right \}\]
La cantidad entre paréntesis se llama la matriz de cumplimiento del material, denotada\(S\) o\(S_{ij}\). Es importante captar el significado físico de sus diversos términos. Directamente a partir de las reglas de multiplicación matricial, el elemento en la\(i^{th}\) fila y\(j^{th}\) columna de\(S_{ij}\) es la contribución de la\(j^{th}\) tensión a la\(i^{th}\) deformación. Por ejemplo, el componente en la posición 1,2 es la contribución de la tensión\(y\) -direction a la deformación\(x\) -direction: multiplicar\(\sigma_y\) por\(1/E\) da la deformación\(y\) -direction generada por\(\sigma_y\), y luego multiplicar esta por\(-\nu\) da la cepa de Poisson inducidos en la\(x\) dirección. Los elementos cero muestran la falta de acoplamiento entre los componentes normal y cortante.
Si queremos escribir las tensiones en términos de las cepas, la Ecuación 4.4.1 se puede invertir para dar:
\[\left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\tau_{xy}} \end{array} \right \} = \dfrac{E}{1- \nu^2} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & (1 - \nu)/2 \end{bmatrix} \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\gamma_{xy}} \end{array} \right \}\]
donde aquí\(G\) ha sido sustituido por\(E/2(1 + \nu)\). Esta relación se puede abreviar más adelante como:
\[\sigma = D \epsilon\]
donde\(D = S^{-1}\) está la matriz de rigidez. Obsérvese que el módulo de Young se puede recuperar tomando el recíproco del elemento 1,1 de la matriz de cumplimiento\(S\), pero que la posición 1,1 de la matriz de rigidez\(D\) contiene efectos de Poisson y no es igual a\(E\).
Materiales Anisotrópicos
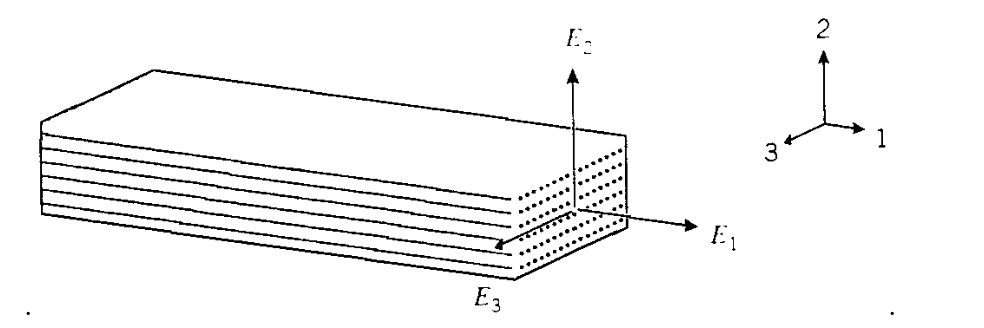
Si el material tiene una textura como madera o compuestos de fibra reforzados unidireccionalmente como se muestra en la Figura 1, el módulo\(E_1\) en la dirección de la fibra será típicamente mayor que aquellos en las direcciones transversales (\(E_2\)y\(E_3\)). Cuando\(E_1 \ne E_2 \ne E_3\), se dice que el material es ortotrópico. Es común, sin embargo, que las propiedades en el plano transversal a la dirección de la fibra sean isotrópicas a una buena aproximación (\(E_2 = E_3\)); dicho material se denomina transversalmente isotrópico. Las leyes constitutivas elásticas deben ser modificadas para dar cuenta de esta anisotropía, y la siguiente forma es una extensión de las ecuaciones habituales de elasticidad isotrópica a materiales transversalmente isotrópicos:
\[\left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ {\gamma_{12}} \end{array} \right \} = \begin{bmatrix} 1/E_1 & -\nu_{21}/E_2 & 0 \\ -\nu_{12}/E_1 & 1/E_2 & 0 \\ 0 & 0 & 1/G_{12} \end{bmatrix} \left \{ \begin{array} {c} {\sigma_1} \\ {\sigma_2} \\ {\tau_{12}} \end{array} \right \}\]
El parámetro\(\nu_{12}\) es la relación principal de Poisson; es la relación de la deformación inducida en la dirección 2 por una deformación aplicada en la dirección 1. Este parámetro no se limita a valores menores a 0.5 como en materiales isotrópicos. Por el contrario,\(\nu_{21}\) da la tensión inducida en la dirección 1 por una deformación aplicada en la dirección 2. Dado que la dirección 2 (transversal a las fibras) suele tener mucha menos rigidez que la dirección 1, una deformación dada en la dirección 1 generalmente desarrollará una deformación mucho mayor en la dirección 2 que la misma deformación en la dirección 2 inducirá una deformación en la dirección 1. De ahí que por lo general tendremos\(\nu_{12} > \nu_{21}\). Hay cinco constantes en la ecuación anterior (\(E_1, E_2, \nu_{12}, \nu_{21}\)y\(G_{12}\). Sin embargo, sólo cuatro de ellos son independientes; ya que la\(S\) matriz es simétrica, tenemos\(\nu_{21}/E_2 = \nu_{12}/E_1\).
La forma simple de la Ecuación 4.4.4, con ceros en los términos que representan el acoplamiento entre componentes normales y cortantes, se obtiene solo cuando los ejes están alineados a lo largo de las direcciones principales del material; es decir, a lo largo y transversal a los ejes de las fibras. Si los ejes están orientados a lo largo de alguna otra dirección, se poblarán todos los términos de la matriz de cumplimiento, y la simetría del material no será evidente. Si por ejemplo la dirección de la fibra está fuera del eje de la dirección de carga, el material desarrollará deformación por cizallamiento a medida que las fibras intentan orientarse a lo largo de la dirección de carga. Por lo tanto, habrá un acoplamiento entre una tensión normal y una deformación por cizallamiento, que no ocurre en un material isotrópico.
Transformación de Ejes
Es importante poder transformar los ejes hacia y desde el marco de “laboratorio” a un\(x - y\) marco de material natural en el que los ejes podrían etiquetarse 1 - 2 correspondientes a las direcciones de fibra y transversal como se muestra en la Figura 2.
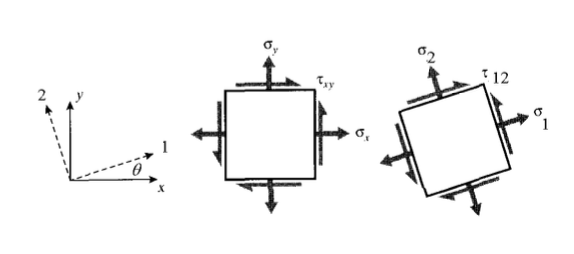
Como se muestra en los libros de texto elementales, la ley de transformación para el estrés cartesiano Cauchy puede escribirse:
\[\begin{array} {rcl} {\sigma_1} & = & {\sigma_x \cos^2 \theta + \sigma_y \sin^2 \theta + 2 \tau_{xy} \sin \theta \cos \theta} \\ {\sigma_2} & = & {\sigma_x \sin^2 \theta + \sigma_y \cos^2 \theta - 2 \tau_{xy} \sin \theta \cos \theta} \\ {\tau_{12}} & = & {(\sigma_y - \sigma_x) \sin \theta \cos \theta + \tau_{xy} (\cos^2 \theta -\sin^2 \theta)} \end{array}\]
Dónde\(\theta\) está el ángulo desde el\(x\) eje hasta el eje 1 (fibra). Estas relaciones se pueden escribir en forma de matriz como
\[\left \{ \begin{array} {c} {\sigma_1} \\ {\sigma_2} \\ {\tau_{12}} \end{array} \right \} = \dfrac{E}{1- \nu^2} \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\tau_{xy}} \end{array} \right \}\]
dónde\(c = \cos \theta\) y\(s = \sin \theta\). Esto se puede abreviar como
\[\sigma' = A \sigma\]
donde\(A\) está la matriz de transformación entre paréntesis arriba. Esta expresión podría aplicarse tanto a estados de tensión tridimensionales como bidimensionales, aunque la forma particular\(A\) dada en la Ecuación 4.4.6 es válida solo en dos dimensiones (tensión plana), y para coordenadas cartesianas.
Usando argumentos matemáticos o geométricos, se puede demostrar que los componentes de la deformación infinitesimal se transforman casi por las mismas relaciones:
\[\left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ {\tfrac{1}{2} \gamma_{12}} \end{array} \right \} = A \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\tfrac{1}{2} \gamma_{xy}} \end{array} \right \} \]
El factor de 1/2 en los componentes de cizallamiento surge de la definición clásica de deformación por cizallamiento, que es el doble de la tensión de cizallamiento tensorial. Esto introduce cierta torpeza en las relaciones de transformación, que se puede reducir introduciendo la matriz de Reuter, definida como
\[[R] = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \ \ or \ \ [R]^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \tfrac{1}{2} \end{bmatrix}\]
Ahora podemos escribir:
\(\left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ { \gamma_{12}} \end{array} \right \} = R \left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ {\tfrac{1}{2} \gamma_{12}} \end{array} \right \} = RA \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\tfrac{1}{2} \gamma_{xy}} \end{array} \right \} = RAR^{-1} \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\gamma_{xy}} \end{array} \right \}\)
o
\[\epsilon' = RAR^{-1} \epsilon\]
La ley de transformación para el cumplimiento ahora se puede desarrollar a partir de las leyes de transformación para tensiones y tensiones. Por transformaciones sucesivas, la deformación en una\(x-y\) dirección arbitraria se relaciona con la deformación en las direcciones 1-2 (material principal), luego con las tensiones en las direcciones 1-2, y finalmente con las tensiones en las\(x-y\) direcciones. La agrupación final de matrices de transformación que relacionan las\(x-y\) deformaciones con las\(x-y\) tensiones es entonces la matriz de conformidad transformada en la\(x-y\) dirección:
\(\left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ { \gamma_{xy}} \end{array} \right \} = R \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\tfrac{1}{2} \gamma_{xy}} \end{array} \right \} = RA^{-1} \left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ {\tfrac{1}{2} \gamma_{12}} \end{array} \right \} = RA^{-1} R^{-1} \left \{ \begin{array} {c} {\epsilon_1} \\ {\epsilon_2} \\ { \gamma_{12}} \end{array} \right \}\)
\(=RA^{-1} R^{-1} S \left \{ \begin{array} {c} {\sigma_1} \\ {\sigma_2} \\ { \tau_{12}} \end{array} \right \} = RA^{-1} R^{-1} SA \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ { \tau_{xy}} \end{array} \right \} \equiv \bar{S} \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ { \tau_{xy}} \end{array} \right \}\)
donde\(\bar{S}\) está la matriz de cumplimiento transformada relativa a\(x-y\) los ejes. La inversa de\(\bar{S}\) es\(\bar{D}\), la matriz de rigidez relativa a\(x-y\) los ejes:
\[\bar{S} = RA^{-1} R^{-1} SA, \ \ \bar{D} = \bar{S}^{-1}\]
Ejemplo\(\PageIndex{1}\)
Considere una capa de compuesto Kevlar-epoxi con una rigidez\(E_1 = 82, E_2 = 4, G_{12} = 2.8\) (todos GPa) y\(\nu_{12} = 0.25\). orientada\(30^{\circ}\) desde el\(x\) eje. La rigidez en la\(x\) dirección se puede encontrar como el recíproco del elemento 1,1 de la matriz de cumplimiento transformada\(S\), como lo da la Ecuación 4.4.11. A continuación se muestra cómo se puede hacer esto con el software de matemáticas simbólicas Maple (editado por brevedad):
Read linear algebra package > with(linalg): Define compliance matrix > S:=matrix(3,3,[[1/E[1],-nu[21]/E[2],0],[-nu[12]/E[1],1/E[2],0],[0,0,1/G[12]]]); Numerical parameters for Kevlar-epoxy > Digits:=4;unprotect(E);E[1]:=82e9;E[2]:=4e9;G[12]:=2.8e9;nu[12]:=.25; nu[21]:=nu[12]*E[2]/E[1]; Compliance matrix evaluated > S2:=map(eval,S);
\(S2 := \begin{bmatrix} .122010^{-10} & -.305010^{-11} & 0 \\ -.304910^{-11} & .250010^{-9} & 0 \\ 0 & 0 & .357110^{-9} \end{bmatrix} \)
Transformation matrix > A:=matrix(3,3,[[c^2,s^2,2*s*c],[s^2,c^2,-2*s*c],[-s*c,s*c,c^2-s^2]]); Trigonometric relations and angle > s:=sin(theta);c:=cos(theta);theta:=30*Pi/180; Transformation matrix evaluated > A2:=evalf(map(eval,A));
\(A2 := \begin{bmatrix} .7500 & .2500 & .8660 \\ .2500 & .7500 & -.8660 \\ -.4330 & .4330 & .5000 \end{bmatrix} \)
Reuter's matrix > R:=matrix(3,3,[[1,0,0],[0,1,0],[0,0,2]]); Transformed compliance matrix > Sbar:=evalf(evalm( R &* inverse(A2) &* inverse(R) &* S2 &* A2 ));
\(Sbar := \begin{bmatrix} .882810^{-10} & -.196810^{-10} & -.122210^{-9} \\ -.196910^{-10} & .207110^{-9} & -.837010^{-10} \\ -.122210^{-9} & -.837710^{-10} & .290510^{-9} \end{bmatrix} \)
Stiffness in x-direction > 'E[x]'=1/Sbar[1,1];
\(E_x = .113310^{11}\)
Tenga en cuenta que la matriz de cumplimiento transformada es simétrica (hasta dentro del error de redondeo numérico), pero que existen valores de acoplamiento distintos de cero. Un usuario no consciente de la composición interna del material lo consideraría completamente anisotrópico.
Placas compuestas laminadas
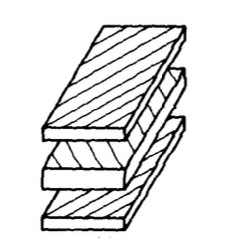
Una de las formas más comunes de materiales compuestos reforzados con fibra es el laminado cruzado, en el que el fabricador “coloca” una secuencia de “capas” reforzadas unidireccionalmente como se indica en la Figura 3. Cada capa es típicamente una lámina delgada (aproximadamente 0.2 mm) de fibras colimadas impregnadas con un epoxi sin curar u otro material de matriz de polímero termoendurecible. La orientación de cada capa es arbitraria, y la secuencia de colocación se adapta para lograr las propiedades deseadas del laminado. En esta sección describimos cómo se diseñan y analizan dichos laminados.
\ Teoría clásica del laminado” es una extensión de la teoría para la flexión de placas homogéneas, pero con un margen para las tracciones en el plano además de los momentos de flexión, y para la rigidez variable de cada capa en el análisis. En casos generales, la determinación de las tracciones y momentos en una ubicación determinada requerirá una solución de las ecuaciones generales para la compatibilidad de equilibrio y desplazamiento de las placas. Esta teoría se trata en una serie de textos estándar (cf. S. Timoshenko y S. Woinowsky-Krieger, Theory of Plates and Shells, McGraw-Hill, Nueva York, 1959.), y no se discutirá aquí.
Comenzamos asumiendo un conocimiento de las tracciones N y momentos M aplicados a una placa en una posición\(x,y\), como se muestra en la Figura 4:
\[N = \left \{ \begin{array} {c} {N_x} \\ {N_y} \\ {N_{xy}} \end{array} \right \} \ \ \ M = \left \{ \begin{array} {c} {M_x} \\ {M_y} \\ {M_{xy}} \end{array} \right \}\]
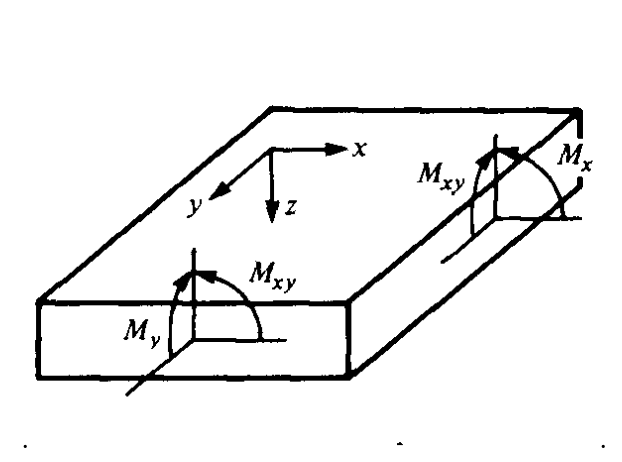
Será conveniente normalizar estas tracciones y momentos por el ancho de la placa, por lo que tienen unidades de\(N/m\) y\(N-m/m\), o simplemente\(N\), respectivamente. Coordina\(x\) y\(y\) son las direcciones en el plano de la placa, y habitualmente\(z\) se toma como positiva hacia abajo. La deflexión en la\(z\) dirección se denomina\(w\), también tomada como positiva hacia abajo.
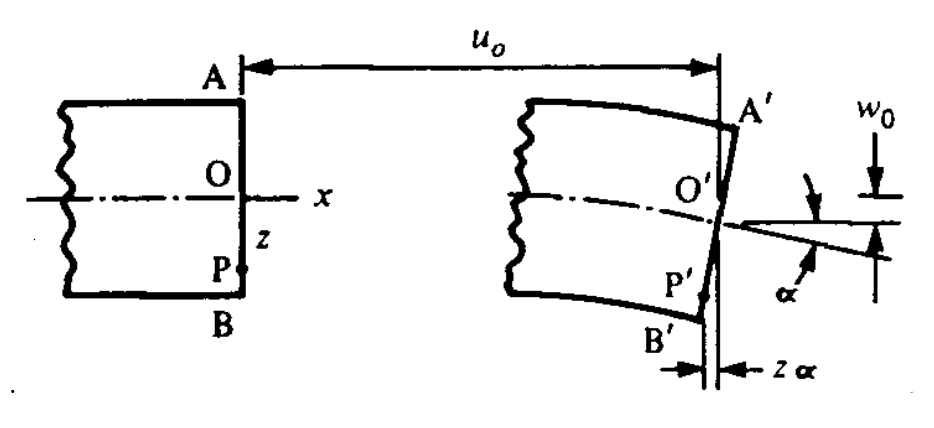
Análogamente con la suposición de Euler para vigas, la suposición de Kirshchoff para flexión de placas toma inicialmente líneas verticales rectas para permanecer rectas pero rotar alrededor del plano medio (\(z = 0\)). Como se muestra en la Figura 5, los desplazamientos horizontales\(u\) y\(v\) en las\(y\) direcciones\(x\) y debido a la rotación pueden tomarse a una aproximación razonable desde el ángulo de rotación y la distancia desde el plano medio, y este desplazamiento rotacional se suma al desplazamiento del plano medio ( \(u_0, v_0\)):
\[u = u_0 - z w_{0, x}\]
\[v = v_0 - z w_{0, y}\]
\[\epsilon = \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ { \gamma_{xy}} \end{array} \right \} = \left \{ \begin{array} {c} {u_{,x}} \\ {v_{,y}} \\ {u_{,y} + v_{,x}} \end{array} \right \} = \left \{ \begin{array} {c} {u_{0,x} - zw_{0,xx}} \\ {v_{0,y} - zw_{0, yy}} \\ {(u_{0,y} + v_{0, x}) - 2z w_{0, xy}} \end{array} \right \} = \epsilon^0 + z\kappa\]
Las deformaciones son solo los gradientes de los desplazamientos; usando notación matricial estos pueden escribirse donde\(\epsilon^0\) está la deformación del plano medio y\(\kappa\) es el vector de segundas derivadas del desplazamiento, llamado la curvatura:
\(\kappa = \left \{ \begin{array} {c} {\kappa_x} \\ {\kappa_y} \\ { \kappa_{xy}} \end{array} \right \} = \left \{ \begin{array} {c} {-w_{0, xx}} \\ {-w_{0, yy}} \\ {-2w_{0, xy}} \end{array} \right \}\)
El componente\(\kappa_{xy}\) es una curvatura de torsión, que indica cómo cambia la pendiente del plano medio\(x\) -direction con\(y\) (o equivalentemente cómo cambia la pendiente\(y\) -direction con\(x\)).
Las tensiones relativas a los\(x-y\) ejes se determinan ahora a partir de las deformaciones, y esto debe tomar en consideración que cada capa tendrá en general una rigidez diferente, dependiendo de sus propias propiedades y también su orientación con respecto a los\(x-y\) ejes. Esto se explica calculando la matriz de rigidez transformada\(\bar{D}\) como se describe en el apartado anterior (Ecuación 4.4.11). Recuerde que las rigideces de las capas dadas por la Ecuación 4.4.4 son aquellas a lo largo de las direcciones de fibra y transversal de esa capa en particular. Las propiedades de cada capa deben transformarse en\(x-y\) ejes comunes, elegidos arbitrariamente para todo el laminado. Las tensiones en cualquier posición vertical son entonces:
\[\sigma = \bar{D} \epsilon = \bar{D} \epsilon^0 + z \bar{D} \kappa\]
donde aquí\(\bar{D}\) está la rigidez transformada de la capa en la posición en la que se calculan las tensiones.
Cada una de estas tensiones de capa debe agregarse para equilibrar la tracción por unidad de ancho\(N\):
\[N = \int_{-h/2}^{+h/2} \sigma dz = \sum_{k = 1}^{N} \int_{z_k}^{z_{k + 1}} \sigma_k dz\]
donde\(\sigma_k\) esta la tension en la capa\(k\) th y\(z_k\) es la distancia desde el plano medio laminado hasta la parte inferior de la capa\(k\) th. Usando la Ecuación 4.4.16 para escribir las tensiones en términos de las deformaciones y curvaturas del plano medio:
\[N = \sum_{k = 1}^{N} (\int_{z_k}^{z_{k + 1}} \bar{D} \epsilon^0 dz + \int_{z_k}^{z_{k + 1}} \bar{D} \kappa z dz)\]
La curvatura\(\kappa\) y la deformación del plano medio\(\epsilon^0\) son constantes en todas partes\(z\), y la rigidez transformada\(\bar{D}\) no cambia dentro de una capa dada. Eliminando estas cantidades de dentro de las integrales:
\[N = \sum_{k = 1}^{N} (\bar{D} \epsilon^0 \int_{z_k}^{z_{k + 1}} dz + \bar{D} \kappa \int_{z_k}^{z_{k + 1}} z dz)\]
Después de evaluar las integrales, esta expresión se puede escribir en la forma compacta:
\[N = \mathcal{A} \epsilon^0 + \mathcal{B} \kappa\]
donde\(\mathcal{A}\) es una “matriz de rigidez extensional” definida como:
\[\mathcal{A} = \sum_{k = 1}^{N} \bar{D} (z_{k + 1} - z_k)\]
y\(\mathcal{B}\) es una “matriz de rigidez de acoplamiento” definida como:
\[\mathcal{B} = \dfrac{1}{2} \sum_{k = 1}^{N} \bar{D} (z_{k + 1}^2 - z_k^2)\]
La justificación de los nombres “extensional” y “acoplamiento” se sugiere por la Ecuación 4.4.20. La\(\mathcal{A}\) matriz da la influencia de una tensión extensional en el plano medio\(\epsilon^0\) en la tracción inplane\(N\), y la\(\mathcal{B}\) matriz da la contribución de una curvatura\(\kappa\) a la tracción. Puede que no sea obvio por qué doblar la placa requerirá una tracción en el plano, o por el contrario, por qué tirar de la placa en su plano hará que se doble. Pero visualice la placa que contiene capas de la misma rigidez, excepto algunas capas de muy bajo módulo en algún lugar por encima de su plano medio. Cuando se tira de la placa, las capas más flexibles por encima del plano medio tenderán a estirarse más que las capas más rígidas debajo del plano medio. La mitad superior del laminado se estira más que la mitad inferior, por lo que adquiere una curvatura cóncava-descendente.
Del mismo modo, los resultados de momento por unidad de ancho deben ser equilibrados por los momentos aportados por las tensiones internas:
\[M = \int_{-h/2}^{+h/2} \sigma z dz = \mathcal{B} \epsilon^0 + \mathcal{D} \kappa\]
donde\(\mathcal{D}\) es una “matriz de rigidez a la flexión” definida como:
\[\mathcal{D} = \dfrac{1}{3} \sum_{k = 1}^{N} \bar{D} (z_{k + 1}^3 - z_k^3)\]
El conjunto completo de relaciones entre fuerzas y momentos aplicados, y las deformaciones y curvaturas del plano medio resultantes, se pueden resumir como una ecuación de matriz única:
\[\left \{ \begin{array} {c} {N} \\ {M} \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix} \left \{ \begin{array} {c} {\epsilon^0} \\ {\kappa} \end{array} \right \}\]
La\(\mathcal{A}/\mathcal{B}/\mathcal{B}/\mathcal{D}\) matriz entre paréntesis es la matriz de rigidez del laminado, y su inversa será la matriz de cumplimiento del laminado.
La presencia de elementos distintos de cero en la matriz de acoplamiento\(\mathcal{B}\) indica que la aplicación de una tracción en el plano conducirá a una curvatura o alabeo de la placa, o que un momento de flexión aplicado también generará una deformación extensional. Estos efectos suelen ser indeseables. Sin embargo, se pueden evitar haciendo que el laminado sea simétrico alrededor del plano medio, como puede revelar el examen de la Ecuación 4.4.22. (En algunos casos, este acoplamiento de extensión-curvatura se puede utilizar como una característica de diseño interesante. Por ejemplo, es posible diseñar una pala de hélice compuesta cuyo ángulo de ataque cambia automáticamente con su velocidad de rotación: el aumento de la velocidad aumenta la carga centrípeta en el plano, lo que induce un giro en la pala.)
Las relaciones anteriores proporcionan un medio sencillo (aunque tedioso, a menos que se utilice una computadora) para determinar tensiones y desplazamientos en materiales compuestos laminados sometidos a cargas de tracción o flexión en el plano:
- Para cada tipo de material en la secuencia de apilamiento, obtenga por medición o estimación micromecánica los cuatro parámetros anisotrópicos independientes que aparecen en la Ecuación 4.4.4: (\(E_1, E_2, \nu_{12}\), y\(G_{12}\)).
- Usando la Ecuación 4.4.11, transforme la matriz de cumplimiento para cada capa de las direcciones principales del material de la capa a algunos ejes de referencia convenientes que se utilizarán para el laminado en su conjunto.
- Invertir la matriz de cumplimiento transformada para obtener la matriz de rigidez transformada (relativa a\(x-y\) los ejes). \(\bar{D}\).
- Agregue la contribución de cada capa a las\(\mathcal{D}\) matrices\(\mathcal{A}, \mathcal{B}\) y según lo prescrito por las Eqns. 4.4.21, 4.4.22 y 4.4.24.
- Ingrese las tracciones prescritas\(N\) y los momentos de flexión\(M\), y forme las ecuaciones del sistema dadas por la Ecuación 4.4.25.
- Resolver el sistema resultante para los valores desconocidos de deformación\(\epsilon^0\) y curvatura en el plano\(\kappa\).
- Utilice la Ecuación 4.4.16 para determinar las tensiones de capa para cada capa en el laminado en términos de\(\epsilon^0, \kappa\) y\(z\). Estas serán las tensiones relativas a los\(x - y\) ejes.
- Utilice la Ecuación 4.4.6 para transformar las\(x - y\) tensiones de nuevo a los ejes principales del material (paralelos y transversales a las fibras).
- Si se desea, las tensiones de capa individuales se pueden usar en un criterio de falla adecuado para evaluar la probabilidad de que esa capa falle. El criterio Tsai-Hill se utiliza popularmente para este propósito:
\[(\dfrac{\sigma_1}{\hat{\sigma}_1})^2 - \dfrac{\sigma_1 \sigma_2}{\hat{\sigma}_1^2} + (\dfrac{\sigma_2}{\hat{\sigma}_2})^2 + (\dfrac{\tau_{12}}{\hat{\tau}_{12}})^2 = 1\]
Aquí\(\hat{\sigma}_1\) y\(\hat{\sigma}_2\) están las resistencias a la tracción de las capas paralelas a y onlong la dirección de la fibra, y\(\hat{\tau}_{12}\) es la resistencia de la capa intralaminar. Este criterio predice el fracaso siempre que el lado izquierdo de la ecuación anterior sea igual o superior a la unidad.
Ejemplo\(\PageIndex{2}\)
El análisis de laminado descrito anteriormente se ha implementado en una placa con nombre de código, y este ejemplo demuestra el uso de este código para determinar la rigidez de una disposición 0/90 de dos capas de compuesto de grafito/epoxi. Aquí a cada una de las dos capas se le da un espesor de 0.5, por lo que la altura total del laminado será la unidad. La teoría del laminado asume un ancho unitario, por lo que las matrices de rigidez y cumplimiento generales se basarán en una sección transversal unitaria.
> plate
assign properties for lamina type 1...
enter modulus in fiber direction...
(enter -1 to stop): 230e9
enter modulus in transverse direction: 6.6e9
enter principal Poisson ratio: .25
enter shear modulus: 4.8e9
enter ply thickness: .5
assign properties for lamina type 2...
enter modulus in fiber direction...
(enter -1 to stop): -1
define layup sequence, starting at bottom...
(use negative material set number to stop)
enter material set number for ply number 1: 1
enter ply angle: 0
enter material set number for ply number 2: 1
enter ply angle: 90
enter material set number for ply number 3: -1
laminate stiffness matrix:
0.1185E+12 0.1653E+10 0.2942E+04 -0.2798D+11 0.0000D+00 0.7354D+03
0.1653E+10 0.1185E+12 0.1389E+06 0.0000D+00 0.2798D+11 0.3473D+05
0.2942E+04 0.1389E+06 0.4800E+10 0.7354D+03 0.3473D+05 0.0000D+00
-0.2798E+11 0.0000E+00 0.7354E+03 0.9876D+10 0.1377D+09 0.2451D+03
0.0000E+00 0.2798E+11 0.3473E+05 0.1377D+09 0.9876D+10 0.1158D+05
0.7354E+03 0.3473E+05 0.0000E+00 0.2451D+03 0.1158D+05 0.4000D+09
laminate compliance matrix:
0.2548E-10 -0.3554E-12 -0.1639E-16 0.7218D-10 0.7125D-19 -0.6022D-16
-0.3554E-12 0.2548E-10 -0.2150E-15 0.3253D-18 -0.7218D-10 -0.1228D-15
-0.1639E-16 -0.2150E-15 0.2083E-09 -0.6022D-16 -0.1228D-15 0.2228D-19
-0.6022E-16 -0.1228E-15 0.2228E-19 -0.1967D-15 -0.2580D-14 0.2500D-08
Tenga en cuenta que este laminado asimétrico genera valores distintos de cero en la matriz de acoplamiento\(\mathcal{B}\), como se esperaba. La rigidez es igual en las\(y\) direcciones\(x\) y, como se puede observar al examinar los elementos 1,1 y 2,2 de la matriz de cumplimiento laminado. El módulo efectivo es\(E_x = E_y = 1/0.2548 \times 10^{-10} = 39.2\) GPa. Sin embargo, el laminado no es isotrópico, como se puede encontrar al volver a ejecutar la placa con la disposición 0/90 orientada en un ángulo diferente a los\(x - y\) ejes.
Efectos de temperatura
Hay una serie de mejoras que uno podría considerar para el código de placa descrito anteriormente: podría extenderse para incluir esfuerzos de cizallamiento interlaminares entre capas, podría incorporar una base de datos de materiales preimpregnados y núcleos disponibles comercialmente, o la interfaz de usuario podría hacerse más amigable” y orientado gráficamente. Muchas de estas características están disponibles en códigos comerciales, o podrían ser agregadas por el usuario, y no se discutirán más aquí. Sin embargo, los efectos de expansión térmica son tan importantes en la aplicación que un código laminado casi debe tener esta característica para ser utilizable, y el enfoque general se esbozará aquí.
En general, un incremento en la temperatura\(\Delta T\) provoca una expansión térmica dada por la relación bien conocida\(\epsilon_T = \alpha \Delta T\), donde\(\epsilon_T\) está la deformación inducida térmicamente y\(\alpha\) es el coeficiente de expansión térmica lineal. Esta deformación térmica se obtiene sin necesidad de aplicar tensión, de manera que cuando se usa la ley de Hooke para calcular la tensión a partir de la deformación, primero se resta el componente térmico:\(\sigma = E(\epsilon - \alpha \Delta T)\). La expansión térmica solo causa deformación normal, por lo que los componentes de cizallamiento de la deformación no se ven afectados. Por lo tanto, la ecuación 4.4.3 se puede extender como
donde el vector de deformación térmica en el marco de coordenadas 1 - 2 es
\(\epsilon_T = \left \{ \begin{array} {c} {\alpha_1} \\ {\alpha_2} \\ {0} \end{array} \right \} \Delta T\)
Aquí\(\alpha_1\) y\(\alpha_2\) están los coeficientes de expansión térmica anisotrópica en las direcciones de fibra y transversal. Transformándose a\(x - y\) ejes comunes, esta relación se convierte en:
\[\left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\tau_{xy}} \end{array} \right \} = \begin{bmatrix} \hat{D}_{11} & \hat{D}_{12} & \hat{D}_{13} \\ \hat{D}_{21} & \hat{D}_{22} & \hat{D}_{23} \\ \hat{D}_{31} & \hat{D}_{32} & \hat{D}_{33} \end{bmatrix} \left \{ \begin{bmatrix} {\epsilon_x} \\ {\epsilon_y} \\ {\epsilon_{xy}} \end{bmatrix} - \begin{bmatrix} {\alpha_x} \\ {\alpha_y} \\ {\alpha_{xy}} \end{bmatrix} \Delta T\right \}\]
Los subíndices en los\(\bar{D}\) elementos se refieren a posiciones de fila y columna dentro de la matriz de rigidez en lugar de direcciones de coordenadas; la barra superior sirve como recordatorio de que estos elementos se refieren a\(x - y\) ejes. El vector de expansión térmica en el lado derecho (\(\alpha = \alpha_x, \alpha_y, \alpha_{xy}\)) es esencialmente un vector de deformación, y así se puede obtener de (\(\alpha_1, \alpha_2, 0\)) como en la Ecuación 4.4.10:
\(\alpha = \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\sigma_{xy}} \end{array} \right \} = RA^{-1} R^{-1} \left \{ \begin{array} {c} {\alpha_1} \\ {\alpha_2} \\ {0} \end{array} \right \}\)
Tenga en cuenta que en la\(x - y\) dirección común, la expansión térmica induce tanto deformaciones normales como de cizallamiento.
El anterior desarrollo independiente de la temperatura ahora puede repetirse, modificarlo solo llevando a lo largo de los términos de expansión térmica. Como antes, el vector de deformación para cualquier posición\(z\) del plano medio se da en términos de la deformación\(\epsilon^0\) y curvatura del plano medio\(\kappa\) por
\(\epsilon = \epsilon^0 + z\kappa\)
El estrés correspondiente es entonces
Equilibrar las tensiones contra las tracciones aplicadas y momentos como antes:
Este resultado es idéntico al de la Ecuación 4.4.20 y la Ecuación 4.4.23, aparte de la adición de las integrales que representan las “cargas térmicas”. Esto permite que los problemas dependientes de la temperatura sean manejados por una “formulación mecánica equivalente”; las ecuaciones generales de gobierno pueden escribirse como
\[\left \{ \begin{array} {c} \bar{N} & \bar{M} \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix} \left \{ \begin{array} {c} \epsilon^0 & \kappa \end{array} \right \}, \ \ \ or \ \ \ \left \{ \begin{array} {c} \epsilon^0 & \kappa \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix}^{-1} \left \{ \begin{array} {c} \bar{N} & \bar{M} \end{array} \right \}\]
donde las\ cargas térmicas equivalentes” se dan como
\(\bar{N} = N + \int \bar{D} \alpha \Delta T dz\)
\(\bar{M} = M + \int \bar{D} \alpha \Delta T z dz\)
La extensión del código de placa para acomodar los efectos térmicos consiste así en modificar el vector de carga de 6\(\times\) 1 añadiendo las dos integrales del vector 3\(\times\) 1 en la expresión anterior.
Efectos Viscoelásticos
Dado que la matriz de muchos laminados compuestos es polimérica, el diseñador puede necesitar considerar la posibilidad de relajación de tensión viscoelástica o fluencia durante la carga. Cualquier efecto de este tipo probablemente no será grande, ya que las fibras que soportan la mayor parte de la carga no suelen ser viscoelásticas. Además, el material de matriz se usa generalmente muy por debajo de su temperatura de transición vítrea, y actuará en un modo elástico vítreo.
Algunas aplicaciones pueden no ser tan simples, sin embargo. Si el laminado se usa a temperatura elevada, y si las tensiones actúan en direcciones no soportadas por las fibras de refuerzo, se pueden observar efectos de relajación. La Figura 6 muestra la fluencia medida en un laminado unidireccional de grafito-epoxi T300/5208 (M.E. Tuttle y H.F. Brinson, “Predicción del cumplimiento de fluencia a largo plazo de lami- nates de compuestos generales”, Experimental Mechanics, p. 89, marzo de 1986.), cargado transversalmente a las fibras a 149\(^{\circ} C\). Incluso en este escenario casi peor de los casos, las deformaciones de fluencia son relativamente pequeñas (menos del 10% de la tensión elástica), pero la Figura 6 muestra que los efectos de relajación pueden ser importantes en algunas situaciones.
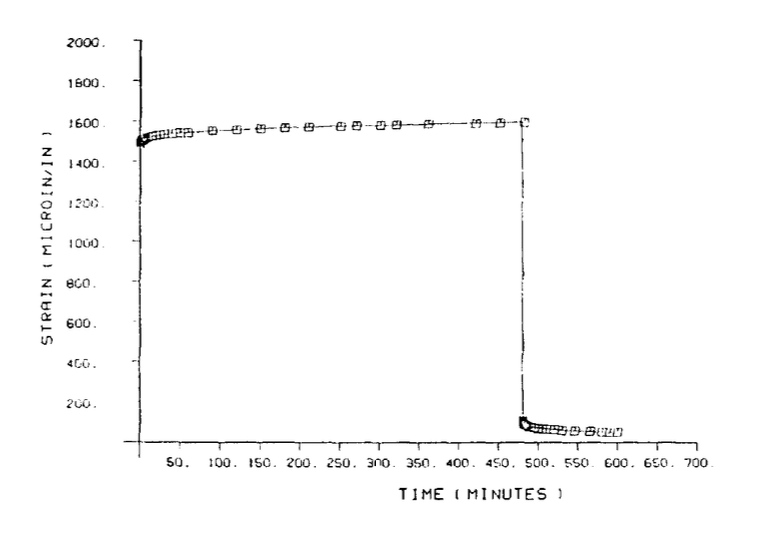
El artículo de Tuttle-Brinson citado anteriormente describe un esquema computacional escalonado en el tiempo que se puede usar para modelar estos efectos de laminado viscoelástico, y aquí se esbozará una forma simplificada de su método. La deformación por fluencia viscoelástica que ocurre en una capa dada durante un incremento de tiempo se\(dt\) puede calcular a partir de la tensión en la capa en ese momento, suponiendo que la capa esté libre de capas adyacentes; esto da una deformación de fluencia de capa independiente. Esta cepa actuará para relajar el estrés de las capas.
Por supuesto, las capas no son libres de deformarse arbitrariamente, y la compatibilidad de deformación adecuada puede restablecerse calculando las cargas externas que producirían deformaciones elásticas iguales a las deformaciones de fluencia de capas independientes. Estas cargas se suman en todas las capas del laminado para dar una carga de fluencia equivalente del laminado. Esta carga se aplica al laminado para calcular un conjunto de deformaciones y curvaturas compatibles, denominadas deformación de fluencia equivalente del laminado. Esta deformación se agrega a la deformación elástica inicial al calcular la tensión en una capa dada, mientras que se resta la deformación por fluencia de capa independiente.
La siguiente lista desarrolla estos pasos con más detalle:
1. Las deformaciones y curvaturas elásticas del plano medio se resuelven para los momentos de flexión y tracciones especificados, utilizando los módulos vítreos de las diversas capas. De la Ecuación 4.4.25:
\(\left \{ \begin{array} {c} \epsilon^0 & \kappa \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix}^{-1} \left \{ \begin{array} {c} N & M \end{array} \right \}\)
2. La deformación elástica en cada capa se obtiene a partir de la Ecuación 4.4.15. Para la\(k^{th}\) capa, con el centro en la coordenada\(z\), esto es:
\(\epsilon_{p\_e\_xy} = \epsilon^0 + z\kappa\)
donde el\(p\_e\_xy\) subíndice indica pliegue, elástico, deformación en la\(x-y\) dirección. Las deformaciones de las capas elásticas en relación con las direcciones 1-2 (fibra-transversal) vienen dadas por la transformación de la Ecuación 4.4.10:
\(\epsilon_{p\_e\_12} = RAR^{-1} \epsilon_{p\_e\_xy}\)
Estos dos primeros pasos se realizan mediante el código de placa elástica, y la adaptación a la respuesta viscoelástica consiste en agregar los siguientes pasos.
3. La tensión actual de la capa\(\sigma_{k\_12}\) en las direcciones 1-2 es:
La cantidad\(\epsilon_{p\_lc\_12} - \epsilon_{p\_c\_12}\) es la diferencia entre la deformación de fluencia del laminado equivalente y la deformación por fluencia de capa independiente. Las cantidades\(\epsilon_{p\_lc\_12}\) y\(\epsilon_{p\_c\_12}\) se establecen en cero inicialmente, pero se actualizan en los pasos 4 y 8 siguientes para dar cuenta de la relajación viscoelástica.
4. La tensión actual de la capa se usa entonces en un modelo viscoelástico apropiado para calcular la fluencia que se produciría si la capa estuviera libre para deformarse independientemente de las capas adyacentes; esto se denomina deformación por fluencia de capa independiente. Para un modelo Voigt simple, el valor actual de deformación por fluencia se puede actualizar a partir de su valor en el paso de tiempo anterior como:
donde los superíndices en la deformación indican valores en los pasos de tiempo actual y anterior. Aquí\(C_v\) está el cumplimiento viscoelástico de fluencia y\(\tau\) es un tiempo de relajación. Una deformación por fluencia igual a\(C_v\) se desarrollará además de la tensión elástica inicial en el laminado, y una fracción\(2/e\) de esta deformación por fluencia se desarrollará en un tiempo\(\tau\). Se\(C_v\) utilizarán diferentes valores de para los componentes de deformación de fibra, transversal y cizallamiento debido a la anisotropía de la capa.
5. Las tensiones en las direcciones 1-2 y\ (x-y) que serían necesarias para desarrollar las deformaciones de fluencia de capa independiente si la capa fuera elástica son
\(\sigma_{k\_12} = D\epsilon_{p\_c\_12}\)
\(\sigma_{k\_xy} = A^{-1} \sigma_{k\_12}\)
6. Estas tensiones de capas elásticas equivalentes se suman sobre todas las capas en el laminado para acumular una carga de fluencia del laminado equivalente. La contribución de la\(k^{th}\) capa es:
\(N_c = N_c + t_k \sigma_{k\_xy}\)
\(M_c = M_c + t_k z \sigma_{k\_xy}\)
donde\(k^{th}\) es el grosor de la\(k^{th}\) capa y\(z\) su coordenada de la línea central.
7. A continuación, se calcula una deformación de fluencia del laminado equivalente a partir de la matriz de elasticidad elástica y las cargas de fluencia del laminado equivalentes como
\(\left \{ \begin{array} {c} \epsilon_{lc}^0 & \kappa_{lc} \end{array} \right \} = \begin{bmatrix} \mathcal{A} & \mathcal{B} \\ \mathcal{B} & \mathcal{D} \end{bmatrix}^{-1} \left \{ \begin{array} {c} N_c & M_c \end{array} \right \}\)
8. La deformación por fluencia del laminado de la capa en las direcciones\(x-y\) y 1-2 son
\(\epsilon_{p\_pc\_xy} = \epsilon_{lc}^0 + z \kappa_{lc}\)
\(\epsilon_{p\_lc\_12} = RAR^{-1} \epsilon_{p\_lc\_xy}\)
9. Finalmente, se incrementa el tiempo\((t \leftarrow t + dt)\) y se calcula otro ciclo de tiempo a partir del paso 3.
Ejemplo\(\PageIndex{3}\)
Como ilustración del algoritmo anterior, considere un laminado modelo simple con una capa isotrópica. Las constantes elásticas son\(E = 100\) (unidades arbitrarias) y\(\nu = 0.25\), y se aplica un esfuerzo unitario en la\(x\) dirección -dirección. Por lo tanto,\(x\) la deformación inicial en dirección es\(\epsilon_{x,0} = \sigma_x/E = 0.01\). En este caso de prueba isotrópica, el código calcula el módulo de cizallamiento como\(G = E/2(1 + \nu)\). La deformación por fluencia se rige por un parámetro\(v_{frac}\), que establece la flexibilidad de fluencia Voigt\(v_{frac}/E_2\) en la dirección transversal,\(v_{frac}/G_{12}\) para los componentes de cizallamiento, y cero en la dirección de la fibra (asumiendo solo una respuesta elástica a lo largo de las fibras).\(G_v\)
La Figura 7 muestra el historial de deformación por fluencia de este laminado para un tiempo de relajación de\(\tau = 1000\) s. El código avanza linealmente en tiempo logarítmico, en este caso con cuatro etapas de tiempo por década. La deformación por fluencia es la tensión más allá de la tensión elástica inicial, que pasa de cero a\(C_v \epsilon_{x,0} = 5 \times 10^{-4}\) medida que el tiempo avanza a través del tiempo de relajación.
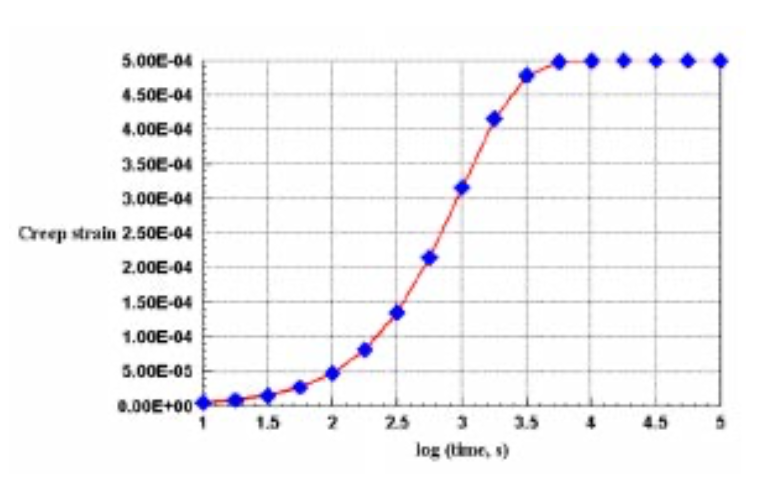
Referencias
- Ashton, J.E., J.C. Halpin y P.H. Petit, Imprimación sobre materiales compuestos: análisis, prensa tecnomica, Westport, CT, 1969.
- Jones, R.M., Mecánica de materiales compuestos, McGraw-Hill, Nueva York, 1975.
- Powell, P.C., Ingeniería con Polímeros, Chapman y Hall, Londres, 1983.
- Roylance, D., Mecánica de Materiales, Wiley & Sons, Nueva York, 1996.
Ejercicio\(\PageIndex{1}\)
Escriba la matriz de cumplimiento\(x-y\) bidimensional\(\bar{S}\) y la matriz de rigidez\(\bar{D}\) (Ecuación 4.4.11) para una sola capa de compuesto de grafito/epoxi con sus fibras alineadas a lo largo de los\(x-y\) ejes.
Ejercicio\(\PageIndex{2}\)
Escriba la matriz de cumplimiento\(x-y\) bidimensional\(\bar{S}\) y la matriz de rigidez\(\bar{D}\) (Ecuación 4.4.11) para una sola capa de compuesto de grafito/epoxi con sus fibras alineadas 30\(^{\circ}\) del\(x\) eje.
Ejercicio\(\PageIndex{3}\)
Trazar el módulo efectivo de Young, medido a lo largo del\(x-\) eje, de una sola capa unidireccional de compuesto grafito-epoxi en función del ángulo entre la dirección de la fibra de la capa y el\(x-\) eje.
Ejercicio\(\PageIndex{4}\)
Usando un lenguaje de programación de su elección, escriba un código laminado similar al código de placa mencionado en el texto, y verifíquelo calculando las matrices de rigidez y cumplimiento del laminado dadas en Ejemplo\(\PageIndex{2}\).
Ejercicio\(\PageIndex{5}\)
Un\((60^{\circ}/0^{\circ}/-60^{\circ})^S\) layup (el\(S\) superíndice indica que las capas se repiten para dar un laminado simétrico) es un ejemplo de lo que se llama laminados “cuasi-isotrópicos”, teniendo iguales rigideces en las\(y\) direcciones\(x\) y, independientemente de la orientación del laminado. Verificar que esto sea así para dos orientaciones de laminado, una teniendo las 0\(^{\circ}\) capas orientadas a lo largo del\(x\) eje y la otra con las 0\(^{\circ}\) capas orientadas a 30\(^{\circ}\) desde el\(x\) eje.
Propiedades mecánicas de los materiales compuestos
La siguiente tabla enumera los valores de propiedades físicas y mecánicas para materiales representativos de capas y núcleos ampliamente utilizados en laminados compuestos reforzados con fibra. Las propiedades de las capas se toman de F.P.Gerstle, “Composites”, Encyclopedia of Polymer Science and Engineering, Wiley, Nueva York, 1991, que deben consultarse para obtener datos de una gama más amplia de materiales. Véase también G. Lubin, Handbook of Composites, Van Nostrand, Nueva York, 1982.
| S-Vidrio/Epoxi | Kevlar/epoxi | HM Grafito/Epoxi | Pino | Espuma rígida Rohacell 51 | |
|
Propiedades Elásticas: \(E_1\), GPa |
|
|
|
|
|
|
Resistencias a la tracción: \(\sigma_1\), MPa |
1800 |
2000 |
1100 |
78 |
1.9 |
|
Resistencias a la compresión: \(\sigma_1\), MPa |
690 |
280 |
620 |
33 |
0.9 |
|
Propiedades Físicas: \(\alpha_1, 10^{-6}/^{\circ} C\) |
2.1 |
-4.0 |
-0.7 |
|
33 |