3.5: Regímenes MOS

Última actualización
Guardar como PDF

Page ID: 86409

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

¡CNX se retira! Los libros de texto de OpenStax siempre estarán disponibles en openstax.org. Los contenidos creados por la comunidad permanecerán visibles hasta agosto de 2022 y luego se trasladarán a Internet Archive. Conoce más aquí

¡La ecuación final de la Sección 3.4 se parece mucho a las\(I \text{-} V\) características de una resistencia! \(I_{d}\)es simplemente proporcional al voltaje de drenaje\(V_{\text{ds}}\). La constante de proporcionalidad depende de las dimensiones del dispositivo,\(W\) y\(L\), como deberían intuitivamente. La corriente aumenta a medida que el transistor se ensancha; disminuye a medida que el transistor se alarga. También depende de\(c_{\text{ox}}\) y\(\mu_{s}\), y de la diferencia entre el voltaje de puerta y el voltaje umbral\(V_{T}\). Tenga en cuenta que si\(V_{\text{gs}}\) ajustamos podemos cambiar la pendiente de la\(I \text{-} V\) curva. ¡Hemos hecho una resistencia controlada por voltaje!

Figura\(\PageIndex{1}\): El\(I\text{-}V\) gráfico MOSFET en el régimen lineal

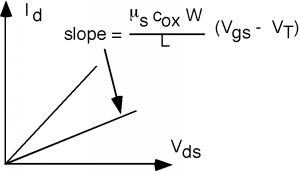
Gráfica de I_d vs V_ds, en el primer cuadrante. El gráfico toma la forma de una línea recta que pasa por el origen, con una pendiente igual al producto de mu_s, c_ox y W dividido por L, el conjunto multiplicado por la diferencia entre V_gs y V_T. — Figura\(\PageIndex{1}\): El\(I\text{-}V\) gráfico MOSFET en el régimen lineal

Se aconseja precaución con este resultado, sin embargo, porque hemos pasado por alto algo bastante importante. Volvamos a nuestra imagen de la puerta y las baterías involucradas en el funcionamiento del transistor MOS. Aquí hemos mostrado explícitamente el canal como una banda negra y hemos introducido una nueva cantidad,\(V_{c} (x)\), el voltaje a lo largo del canal, y una coordenada\(x\), que nos indica dónde estamos en el canal con relación a la fuente y el drenaje. Tenga en cuenta que una vez que aplicamos un potencial de fuente de drenaje\(V_{\text{ds}}\), el potencial en el canal\(V_{c} (x)\) cambia con la distancia a lo largo del canal. Al final de la fuente,\(V_{c}(0) = 0\) ya que la fuente está puesta a tierra. En el extremo de drenaje,\(V_{c}(L) = V_{\text{ds}}\). Definiremos un voltaje\(V_{\text{gc}}\), que es la diferencia de potencial entre el voltaje de puerta y el voltaje en el canal. \[V_{\text{gc}} (x) \equiv V_{\text{gs}} - V_{c} (x)\]

Así,\(V_{\text{gc}}\) va desde\(V_{\text{gs}}\) en el extremo fuente hasta\(V_{\text{gs}} - V_{\text{ds}}\) en el extremo de drenaje.

Figura\(\PageIndex{2}\): Efecto de\(V_{\text{ds}}\) sobre el potencial del canal

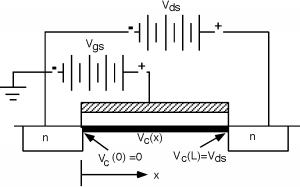
Transistor MOSFET polarizado con la fuente a la izquierda y el drenaje a la derecha. El voltaje del canal entre la fuente y el drenaje es una función de x, la distancia desde el borde izquierdo del canal. En x=0, el voltaje del canal es 0; en x=L, en el borde derecho del canal, el voltaje del canal es V_ds. — Figura\(\PageIndex{2}\): Efecto de\(V_{\text{ds}}\) sobre el potencial del canal

La densidad de carga neta en el canal depende de la diferencia de potencial entre la puerta y el canal en cada punto a lo largo del canal, no solo\(V_{\text{gs}} - V_{T}\). Así tenemos que modificar la ecuación de otro módulo para tener esto en cuenta. \[\begin{array}{l} Q_{\text{chan}} &= c_{\text{ox}} \left(V_{\text{gc}} (x) - V_{T}\right) \\ &= c_{\text{ox}} \left(V_{\text{gs}} - V_{c} (x) - V_{T}\right) \end{array}\]

Esto, a su vez, modifica la relación integral entre\(I_{d}\) y\(V_{\text{gs}}\). \[\int\limits_{0}^{V_{\text{ds}}} \mu_{s} c_{\text{ox}} \left(V_{\text{gs}} - V_{T} - V_{c}(x) \right) W \ dV_{c} (x) = \int\limits_{0}^{L} I_{d} \ dx\]

\(\PageIndex{3}\)La ecuación es solo un poco más difícil de integrar que la anterior, y obtenemos para la corriente de drenaje\[I_{d} = \frac{\mu_{s} c_{\text{ox}} W}{L} \left( \left(V_{\text{gs}}-V_{T}\right) V_{\text{ds}} - \frac{V_{\text{ds}}{ }^2}{2} \right)\]

Esta ecuación se llama la Ecuación Sah después de C.T. Sah, quien describió por primera vez el funcionamiento del transistor MOS de esta manera en 1964. Es muy importante porque describe el comportamiento básico del transistor MOS.

Obsérvese que para valores pequeños de\(V_{\text{ds}}\), una ecuación y Ecuación anteriores nos\(\PageIndex{4}\) darán el mismo\(I_{d} \text{-} V_{\text{ds}}\) comportamiento, porque podemos ignorar el\(V_{\text{ds}}{ }^2\) término en Ecuación\(\PageIndex{4}\). Esto se llama régimen lineal porque tenemos una relación lineal entre la corriente de drenaje y la tensión drenaje-fuente. Sin embargo, a medida que\(V_{\text{ds}}\) comience a hacerse más grande, el término cuadrado comenzará a entrar en juego y la trama comenzará a curvarse. Obviamente, algo está provocando que la corriente caiga a medida que\(V_{\text{ds}}\) se hace más grande. Esto se debe a que la diferencia de voltaje entre la puerta y el canal es cada vez menor, lo que significa que hay menos carga en el canal para proporcionar conducción. Podemos mostrar esto gráficamente haciendo que la capa del canal se vea más delgada a medida que nos movemos de la fuente al drenaje. Ecuación\(\PageIndex{4}\), y de hecho, Figura nos\(\PageIndex{3}\) haría pensar que si\(V_{\text{ds}}\) se hace lo suficientemente grande, que la corriente de drenaje\(I_{d}\) debería empezar a disminuir de nuevo, ¡y tal vez incluso llegar a ser negativa! Esto no parece muy intuitivo, así que echemos un vistazo con más detalle al lugar donde\(I_{d}\) se convierte en un máximo. Podemos definir\(V_{\text{d sat}}\) como el voltaje fuente-drenaje donde\(I_{d}\) se convierte en un máximo. Podemos encontrar esto tomando la derivada de\(I_{d}\) con respecto a\(V_{\text{ds}}\) y fijando la derivada a\(0\). \[\begin{array}{l} \frac{d}{d V_{\text{ds}}} \left(I_{d}\right) &= 0 \\ &= \frac{\mu_{s} c_{\text{ox}} W}{L} \left(V_{\text{gs}} - V_{T} - V_{\text{d sat}} \right) \end{array}\]

Al soltar constantes: \[V_{\text{d sat}} = V_{\text{gs}} - V_{T}\]

Reorganizar esta ecuación nos da un poco más de idea de lo que está pasando. \[\begin{array}{l} V_{\text{gs}} - V_{\text{d sat}} &= V_{T} \\ &= V_{\text{gc}} (L) \end{array}\]

Figura\(\PageIndex{3}\):\(I\text{-}V\) características que muestran la entrega

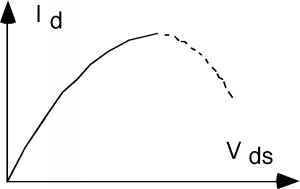
Gráfica de I_d vs V_ds, en el primer cuadrante. La gráfica curva toma la forma de una parábola cóncava-descendente que comienza en el origen, hasta que se alcanza el máximo de la parábola; para valores mayores de V_ds, la forma general de la parábola continúa, pero la gráfica se divide en muchos segmentos cortos. — Figura\(\PageIndex{3}\):\(I\text{-}V\) características que muestran la entrega

Figura\(\PageIndex{4}\): Efecto de\(V_{\text{ds}}\) sobre el canal

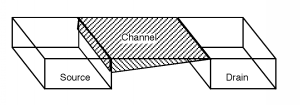
Vista en perspectiva de la fuente de prisma rectangular y drenaje, ubicados a la izquierda y a la derecha respectivamente. El canal entre ellos se representa como un prisma triangular derecho, con la cara superior enrasada con las caras superiores de la fuente y drenaje, la base del triángulo ubicada adyacente a la fuente, y el vértice del triángulo está tocando la esquina superior izquierda del drenaje. — Figura\(\PageIndex{4}\): Efecto de\(V_{\text{ds}}\) sobre el canal

En el extremo de drenaje del canal, cuando\(V_{\text{ds}}\) solo es igual\(V_{\text{d sat}}\), la diferencia entre el voltaje de puerta y el voltaje del canal,\(V_{\text{gc}} (L)\) es justo igual a\(V_{T}\), el voltaje umbral. Cualquier aumento adicional\(V_{\text{ds}}\) y la diferencia entre la puerta y el canal (en la región del canal justo cerca del drenaje) caerá por debajo del voltaje umbral. Esto significa que cuando se\(V_{\text{ds}}\) hace más grande que\(V_{\text{d sat}}\), ¡el canal justo cerca de la región de drenaje desaparece! Ya no tenemos suficiente voltaje entre la puerta y la región del canal para mantener una capa de inversión, por lo que simplemente volvemos a una condición de agotamiento. Esto se llama pellizcar, como se ve en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Canal en pellizco

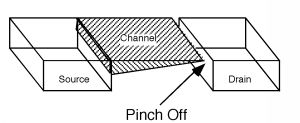
Canal en pellizco: similar a la Figura 4 desde arriba, pero con el canal no extendiéndose hasta el desagüe. Existe un pequeño hueco entre el drenaje y el vértice del prisma triangular derecho del canal. — Figura\(\PageIndex{5}\): Canal en pellizco

¿Qué pasa con la corriente de drenaje cuando golpeamos pellizcar? Parece que podría llegar a cero, ¡pero esa no es la respuesta correcta! A pesar de que no hay un canal activo en la región de pinch-off, todavía hay silicio — simplemente pasa a estar agotado de todos los portadores libres. Hay un campo eléctrico que va desde el drenaje hasta el canal, y cualquier electrón que se mueva a lo largo del canal hasta la región de pellizco es aspirado por el campo y entra en el drenaje. Esto es igual que la corriente que fluye en la condición de saturación inversa de un diodo. No hay portadores libres en la región de agotamiento del diodo, pero\(I_{\text{sat}}\) fluye a través de la región de unión.

Bajo condiciones de pellizco, aumentos adicionales en\(V_{\text{ds}}\), no da como resultado más corriente de drenaje. Se puede pensar en el canal pellizcado como una resistencia, con un voltaje de\(V_{\text{d sat}}\) a través de él. Cuando\(V_{\text{ds}}\) se hace más grande que\(V_{\text{d sat}}\), el exceso de voltaje aparece a través de la región de pellizco, y el voltaje a través del canal permanece fijo en\(V_{\text{d sat}}\). Si el canal mantiene la misma carga, y tiene el mismo voltaje a través de él, entonces la corriente a través del canal (y hacia el drenaje) permanecerá fija, a un valor que llamaremos\(I_{\text{d sat}}\).

Hay otra figura que a veces ayuda a ver lo que está pasando. Vamos a trazar la energía potencial para un electrón, a medida que atraviesa el canal. Dado que la fuente está a potencial cero y el drenaje está en\(V_{\text{ds}}\), un electrón perderá energía potencial a medida que fluye de la fuente al drenaje. La figura\(\PageIndex{6}\) muestra algunos ejemplos para varios valores de\(V_{\text{ds}}\):

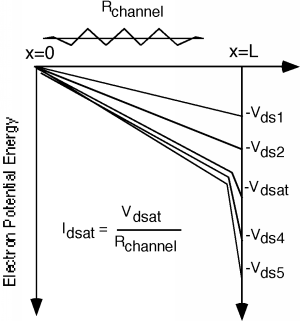
Al pasar de la fuente al drenaje, la energía potencial de electrones disminuye. La gráfica toma la forma de líneas rectas con pendientes relativamente poco profundas que van de 0 a -v_DS1 y -V_DS2; para alcanzar los valores de -v_DSAT, -v_DS4 y -V_DS5, la gráfica tiene pendientes poco profundas para la mayor parte de la longitud del canal antes de pasar bruscamente a una pendiente más pronunciada para la última porción. — Figura\(\PageIndex{6}\): Caída de energía potencial de electrones que va de fuente a drenaje.

Para los dos primeros voltajes de drenaje,\(V_{\text{ds}1}\) y\(V_{\text{ds}2}\), estamos por debajo del pinch-off, y así la caída de voltaje a través\(R_{\text{channel}}\) aumenta a medida que\(R_{\text{channel}}\) aumenta, y por lo tanto, también lo hace\(I_{d}\). En\(V_{\text{d sat}}\), acabamos de llegar al pinch-off, y estamos empezando a ver que la región de agotamiento del “campo alto” comienza a desarrollarse. Dado que el campo eléctrico es solo la derivada del potencial, la pendiente de las curvas en Figura te\(\PageIndex{6}\) da una idea de cuán grande será el campo eléctrico. Para mayores aumentos en\(V_{\text{ds}}\), como\(V_{\text{ds}4}\) y\(V_{\text{ds}5}\) todo el voltaje adicional solo aparece como una caída de campo alta al final del canal. La caída de voltaje a través de la parte conductora del canal permanece fija (más o menos) en\(V_{\text{d sat}}\) y así la corriente de drenaje permanece más o menos fija en\(I_{\text{d sat}}\). Sustituyendo la expresión por\(V_{\text{sat}}\) en la expresión for\(I_{d}\), podemos obtener una expresión para\(I_{\text{d sat}}\):\[I_{\text{d sat}} = \frac{\mu_{s} c_{\text{ox}} W}{2L} \left(V_{\text{gs}} - V_{T}\right)^{2}\]

Podemos definir una nueva constante,\(k\), donde\[k = \frac{\mu_{s} c_{\text{ox}} W}{L}\]

Así que \[I_{\text{d sat}} = \frac{k}{2} \left(V_{\text{gs}} - V_{T}\right)^{2}\]

Lo que esto significa para Figura\(\PageIndex{3}\) es que cuando\(V_{\text{ds}}\) llega a\(V_{\text{d sat}}\), simplemente nos mantenemos\(I_{d}\) fijos a partir de entonces, con un valor de\(I_{\text{d sat}}\). Para diferentes valores de\(V_{g}\), el voltaje de puerta, vamos a tener una\(I_{d} \text{-} V_{\text{ds}}\) curva diferente, y así una vez más, terminamos con una familia de “curvas características” para el MOSFET. Estos se muestran en la Figura\(\PageIndex{8}\).

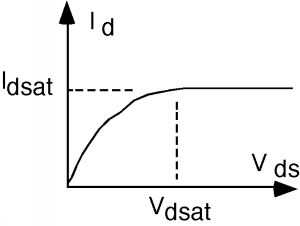
Figura\(\PageIndex{7}\):\(I\text{-}V\) Curva completa para el MOSFET

Gráfica de I_d vs V_ds, en el primer cuadrante.Comenzando en el origen, la gráfica se eleva en una parábola cóncava-descendente que transita suavemente a una línea horizontal en el punto (V_DSAT, I_DSAT). — Figura\(\PageIndex{7}\):\(I\text{-}V\) Curva completa para el MOSFET

Figura\(\PageIndex{8}\): Curvas características para un MOSFET

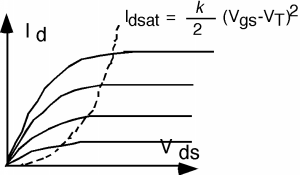
Conjunto de curvas características para un MOSFET, con cada una siguiendo el patrón de la curva de la Figura 7 anterior con pendiente variable para las curvas iniciales y pendientes variables para las porciones lineales posteriores. — Figura\(\PageIndex{8}\): Curvas características para un MOSFET

Esto también nos da una manera bastante fácil en la que “bosquejar” un conjunto de curvas características para un dispositivo dado. Supongamos que tenemos un transistor de efecto de campo MOS que tiene un voltaje umbral de 2 voltios, un ancho de 10 micrones, y una longitud de canal de 1 micra, un espesor de óxido de 150 angstroms, y una movilidad superficial de\(400 \ \frac{\mathrm{C}}{\mathrm{V} \cdot \mathrm{sec}}\). Usando\(\varepsilon_{\text{ox}} = 3.3 \times 10^{-13} \ \frac{\mathrm{F}}{\mathrm{cm}}\), obtenemos un valor de\(2.2 \times 10^{-7} \ \frac{\mathrm{F}}{\mathrm{C}}\) for\(c_{\text{ox}}\). Esto hace entonces\(k\) tener un valor de\[\begin{array}{l} k &= \frac{\mu_{s} c_{\text{ox}} W}{L} \\ &= \frac{400 \cdot 2.2 \times 10^{-7} \cdot 10}{1} \\ &= 8.8 \times 10^{-4} \ \frac{\mathrm{amp}}{\mathrm{volt}^2} \end{array}\]