3.6: Trazado MOS I-V

Ahora utilizamos dos de las ecuaciones (3.5.6 y 3.5.10) que encontramos en la discusión sobre Regímenes MOS para calcular un conjunto de$V_{\text{d sat}}$ y$I_{\text{d sat}}$ valores para diversos valores de$V_{\text{gs}}$. (Tenga en cuenta que$V_{\text{gs}}$ debe ser mayor que$V_{T}$ para que las dos ecuaciones sean válidas.) Cuando obtenemos los números, construimos una mesita.

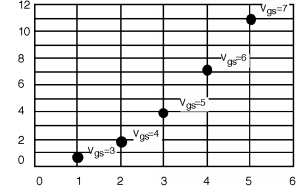
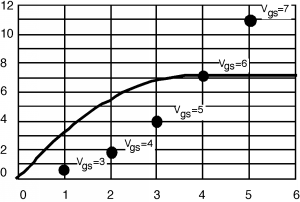
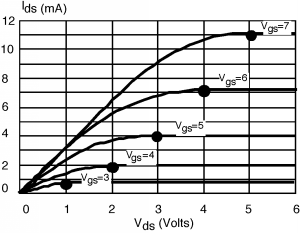
Una vez que tenemos los números (Tabla$\PageIndex{1}$, luego dibujamos un trozo de papel cuadriculado con la escala adecuada, y trazamos los puntos en él. Una vez determinados los$\left(I_{\text{d sat}}, \ V_{\text{d sat}}\right)$ puntos, es fácil de esbozar en el$I\text{-}V$ comportamiento. Simplemente dibujas una curva desde el origen hasta cualquier punto dado, teniéndola “pico hacia fuera” justo en el punto, y luego dibujas una línea recta en$I_{\text{d sat}}$ para terminar las cosas. Una de esas curvas se muestra en la Figura$\PageIndex{2}$. Y luego finalmente en Figura$\PageIndex{3}$ están todos esbozados en. Tus curvas probablemente no serán exactamente correctas pero serán lo suficientemente buenas para muchas aplicaciones.

Tabla$\PageIndex{1}$: Resultados del cálculo$V_{\text{d sat}}$ y$I_{\text{d sat}}$

$V_{\text{gs}}$	$V_{\text{d sat}} \ (\mathrm{V})$	$I_{\text{d sat}} \ (\mathrm{mA})$
\ (V_ {\ texto {gs}}\) ">$3$	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">$1$	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">$0.44$
\ (V_ {\ texto {gs}}\) ">$4$	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">$2$	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">$1.76$
\ (V_ {\ texto {gs}}\) ">$5$	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">$3$	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">$3.96$
\ (V_ {\ texto {gs}}\) ">$6$	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">$4$	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">$7.04$
\ (V_ {\ texto {gs}}\) ">$7$	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">$5$	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">$11$

Figura$\PageIndex{1}$: Trazado$I_{\text{d sat}}$ y$V_{\text{d sat}}$.

Figura$\PageIndex{2}$: Esbozo en una de las$I\text{-}V$ curvas.

Figura$\PageIndex{3}$: El conjunto completo de curvas.

Existe una manera particularmente fácil de medir por$k$ y$V_{T}$ para un MOSFET. Primero introduzcamos el símbolo esquemático para el MOSFET; parece Figura$\PageIndex{4}$. Tomemos un MOSFET y lo conectemos como se muestra en la Figura$\PageIndex{5}$.

Figura$\PageIndex{4}$: Símbolo esquemático para un MOSFET

Figura$\PageIndex{5}$: Circuito para encontrar$V_{T}$ y$k$

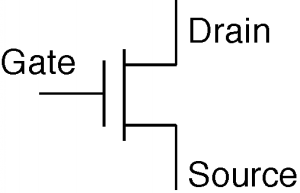
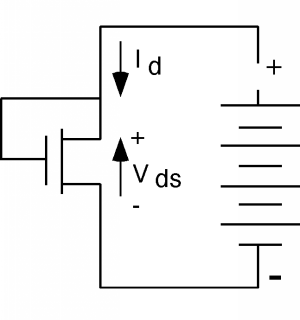
Dado que la puerta de este transistor está conectada al desagüe, no cabe duda de que$V_{\text{gs}} - V_{\text{ds}}$ es menor que$V_{T}$. De hecho, ya que$V_{\text{gs}} = V_{\text{ds}}$, su diferencia es cero. Así, para cualquier valor de$V_{\text{ds}}$, este transistor está operando en su condición saturada. Ya que$V_{\text{gs}} = V_{\text{ds}}$, podemos reescribir una ecuación anterior derivada de la sección sobre regímenes MOS como

$$I_{d} = \frac{k}{2} \left(V_{\text{ds}} - V_{T}\right)^{2}$$

Ahora tomemos la raíz cuadrada de ambos lados:

$$\sqrt{I_{d}} = \sqrt{\frac{k}{2}} \left(V_{\text{ds}} - V_{T}\right)$$

Entonces, si hacemos una trama de$\sqrt{I_{d}}$ en función de$V_{\text{ds}}$, deberíamos obtener una línea recta, con una pendiente de$\sqrt{\frac{k}{2}}$ y una$x$ -intercepción de$V_{T}$.

Figura$\PageIndex{6}$: Obtención$V_{T}$ y$k$

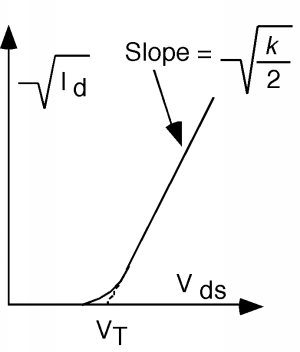
Debido a la no idealidad esperada, la curva no va hasta el final$V_{T}$, sino que se desvía un poco cerca del fondo. Sin embargo, una simple extrapolación lineal de la parte recta de la gráfica produce un valor inequívoco para el voltaje umbral$V_{T}$.