3.6: Trazado MOS I-V

Última actualización
Guardar como PDF

Page ID: 86354

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

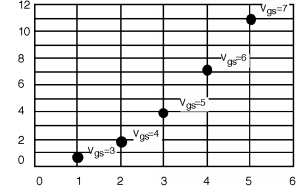
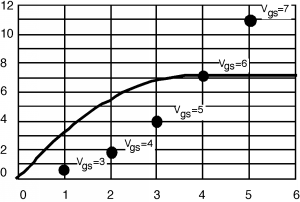
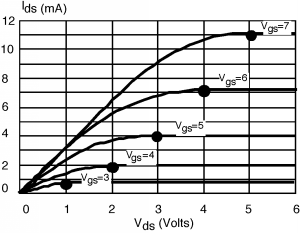
Una vez que tenemos los números (Tabla\(\PageIndex{1}\), luego dibujamos un trozo de papel cuadriculado con la escala adecuada, y trazamos los puntos en él. Una vez determinados los\(\left(I_{\text{d sat}}, \ V_{\text{d sat}}\right)\) puntos, es fácil de esbozar en el\(I\text{-}V\) comportamiento. Simplemente dibujas una curva desde el origen hasta cualquier punto dado, teniéndola “pico hacia fuera” justo en el punto, y luego dibujas una línea recta en\(I_{\text{d sat}}\) para terminar las cosas. Una de esas curvas se muestra en la Figura\(\PageIndex{2}\). Y luego finalmente en Figura\(\PageIndex{3}\) están todos esbozados en. Tus curvas probablemente no serán exactamente correctas pero serán lo suficientemente buenas para muchas aplicaciones.

Tabla\(\PageIndex{1}\): Resultados del cálculo\(V_{\text{d sat}}\) y\(I_{\text{d sat}}\)
\(V_{\text{gs}}\)	\(V_{\text{d sat}} \ (\mathrm{V})\)	\(I_{\text{d sat}} \ (\mathrm{mA})\)
\ (V_ {\ texto {gs}}\) ">\(3\)	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">\(1\)	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">\(0.44\)
\ (V_ {\ texto {gs}}\) ">\(4\)	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">\(2\)	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">\(1.76\)
\ (V_ {\ texto {gs}}\) ">\(5\)	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">\(3\)	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">\(3.96\)
\ (V_ {\ texto {gs}}\) ">\(6\)	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">\(4\)	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">\(7.04\)
\ (V_ {\ texto {gs}}\) ">\(7\)	\ (V_ {\ texto {d sat}}\ (\ mathrm {V})\) ">\(5\)	\ (I_ {\ texto {d sat}}\ (\ mathrm {mA})\) ">\(11\)

Figura\(\PageIndex{1}\): Trazado\(I_{\text{d sat}}\) y\(V_{\text{d sat}}\).

Puntos de la Tabla 3.6.1, trazados en un eje x de V_DSAT en voltios y un eje y de i_DSAT en miliamperios. — Figura\(\PageIndex{1}\): Trazado\(I_{\text{d sat}}\) y\(V_{\text{d sat}}\).

Figura\(\PageIndex{2}\): Esbozo en una de las\(I\text{-}V\) curvas.

Una de las curvas I-V se dibuja en la gráfica de la Figura 1 anterior. Una curva cóncava-descendente comienza en el origen y alcanza su máximo en el punto V_gs=6, y pasa suavemente a una línea horizontal recta a la derecha. — Figura\(\PageIndex{2}\): Esbozo en una de las\(I\text{-}V\) curvas.

Figura\(\PageIndex{3}\): El conjunto completo de curvas.

Curvas I-V dibujadas para todos los puntos trazados de la tabla anterior. Cada curva sigue el patrón de su punto trazado formando el máximo de una curva cóncava-descendente a partir del origen, transitando suavemente a una línea horizontal para valores mayores de V_DSAT. — Figura\(\PageIndex{3}\): El conjunto completo de curvas.

Existe una manera particularmente fácil de medir por\(k\) y\(V_{T}\) para un MOSFET. Primero introduzcamos el símbolo esquemático para el MOSFET; parece Figura\(\PageIndex{4}\). Tomemos un MOSFET y lo conectemos como se muestra en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{4}\): Símbolo esquemático para un MOSFET

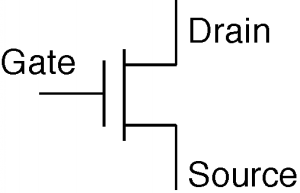
Símbolo esquemático MOSFET para un diagrama de circuito. La puerta está representada por una línea horizontal corta, su punto final derecho intersecando el punto medio de una línea vertical corta. Una corta distancia a la derecha es una línea vertical más larga. Dos líneas horizontales cortas se extienden desde esta línea, hacia la derecha. Una línea vertical se extiende hacia arriba desde el extremo derecho de la línea horizontal superior; esto representa el drenaje. Otra línea vertical se extiende hacia abajo desde el extremo derecho de la línea horizontal inferior; esto representa la fuente. — Figura\(\PageIndex{4}\): Símbolo esquemático para un MOSFET

Figura\(\PageIndex{5}\): Circuito para encontrar\(V_{T}\) y\(k\)

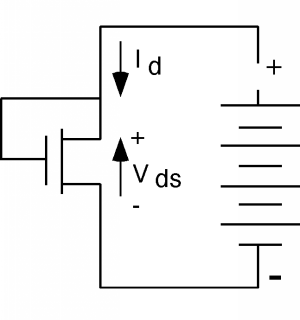
Una fuente de voltaje tiene corriente I_d que fluye fuera de su extremo positivo y entra en una unión donde una rama se conecta a la puerta de un MOSFET y la otra rama se conecta al drenaje del MOSFET. La fuente del MOSFET está conectada al extremo negativo de la fuente de voltaje. Hay una caída de voltaje de V_ds entre el drenaje y la fuente. — Figura\(\PageIndex{5}\): Circuito para encontrar\(V_{T}\) y\(k\)

Dado que la puerta de este transistor está conectada al desagüe, no cabe duda de que\(V_{\text{gs}} - V_{\text{ds}}\) es menor que\(V_{T}\). De hecho, ya que\(V_{\text{gs}} = V_{\text{ds}}\), su diferencia es cero. Así, para cualquier valor de\(V_{\text{ds}}\), este transistor está operando en su condición saturada. Ya que\(V_{\text{gs}} = V_{\text{ds}}\), podemos reescribir una ecuación anterior derivada de la sección sobre regímenes MOS como\[I_{d} = \frac{k}{2} \left(V_{\text{ds}} - V_{T}\right)^{2}\]

Ahora tomemos la raíz cuadrada de ambos lados:\[\sqrt{I_{d}} = \sqrt{\frac{k}{2}} \left(V_{\text{ds}} - V_{T}\right)\]

Entonces, si hacemos una trama de\(\sqrt{I_{d}}\) en función de\(V_{\text{ds}}\), deberíamos obtener una línea recta, con una pendiente de\(\sqrt{\frac{k}{2}}\) y una\(x\) -intercepción de\(V_{T}\).

Figura\(\PageIndex{6}\): Obtención\(V_{T}\) y\(k\)

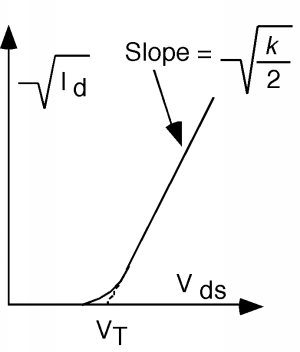
La gráfica de la raíz cuadrada de I_d vs V_ds, en el primer cuadrante, toma la forma de una pequeña curva cóncava-ascendente que se eleva desde un punto a lo largo del eje x transitando suavemente a una línea cuya pendiente es la raíz cuadrada de la mitad de k Si esta porción lineal de la gráfica se extiende, intercepta el eje x en el punto V_T. — Figura\(\PageIndex{6}\): Obtención\(V_{T}\) y\(k\)

Debido a la no idealidad esperada, la curva no va hasta el final\(V_{T}\), sino que se desvía un poco cerca del fondo. Sin embargo, una simple extrapolación lineal de la parte recta de la gráfica produce un valor inequívoco para el voltaje umbral\(V_{T}\).