Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

3.7: Modelos

Última actualización

30 oct 2022
Guardar como PDF
- 3.6: Trazado MOS I-V
- 3.8: Inversores y Lógica

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

¡CNX se jubila! Los libros de texto de OpenStax siempre estarán disponibles en openstax.org. El contenido creado por la comunidad permanecerá disponible hasta agosto de 2022 y luego se trasladará a Internet Archive. Conoce más aquí

Una segunda, y algunas personas piensan más precisa, la manera de encontrar $V_{T}$ es mirar las características del transistor MOS en su régimen lineal. El circuito de prueba se parece a lo que se ve en la Figura $\PageIndex{1}$ . En este caso, $V_{\text{ds}}$ se mantiene bastante pequeño (0.2 Voltios más o menos) y el voltaje de la puerta $V_{\text{gs}}$ se barre en algún rango. Si miras hacia atrás a esta ecuación en otro módulo, podemos reescribirla ligeramente para ver que

$I_{d} = \frac{\mu_{s} c_{\text{ox}} W V_{\text{ds}}}{L} \left(V_{\text{gs}} - V_{T}\right)$

Esta ecuación obviamente nos dará una gráfica lineal de $I_{d}$ como una función de $V_{\text{gs}}$ , que se verá algo así como Figura $\PageIndex{2}$ . Obviamente, se trata de un dispositivo con un voltaje umbral de aproximadamente 2 voltios. ¿Puedes averiguar qué $k$ es para este transistor? Si no, regresa y vuelve a leer algunas cosas.

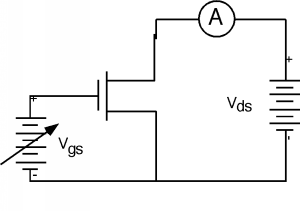
Figura $\PageIndex{1}$ : Circuito para encontrar $V_{T}$

Un MOSFET tiene el extremo positivo de una fuente de voltaje V_gs conectada a su puerta. Su drenaje se conecta al extremo positivo de una fuente de voltaje V_ds, con un amperímetro que mide la corriente que sale del drenaje. Los extremos negativos de ambas fuentes de voltaje están conectados a la fuente del MOSFET. — Figura $\PageIndex{1}$ : Circuito para encontrar $V_{T}$

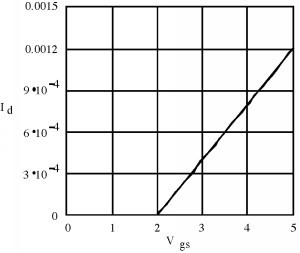
Gráfica de I_d en amperios vs V_gs en voltios. La trama toma la forma de una línea que discurre entre los puntos (2, 0) y (5, 0.0012). — Figura $\PageIndex{2}$ : $I_{d}$ como una función de $V_{\text{gs}}$ para un transistor MOS en el rango lineal

Ahora abordemos una cuestión fundamental referente a todo esto: ¿Y qué? ¿Qué tenemos aquí? Una respuesta es que tenemos otro dispositivo que de alguna manera se parece al transistor bipolar que estudiamos en el último capítulo. En el régimen de saturación, el dispositivo se ve y actúa como una fuente de corriente, y probablemente podría usarse como amplificador. Es bastante fácil hacer un modelo de señal pequeña. El drenaje actúa como una fuente de corriente, que es controlada por $V_{\text{gs}}$ . ¿Qué debemos hacer con respecto a la terminal de la puerta? La puerta realmente no está conectada a nada dentro del transistor, por lo que se ve como un circuito abierto. (De hecho, hay una capacitancia $C_{\text{gate}} = c_{\text{ox}} A_{\text{gate}}$ donde $A_{\text{gate}} = WL$ , el área de la puerta, pero en la mayoría de las aplicaciones lineales de baja frecuencia, esta capacitancia no es significativa.) Así nuestro modelo de señal pequeña para el MOSFET, si está operando en el modo de saturación, es como se ve en la Figura $\PageIndex{3}$ .

Figura $\PageIndex{3}$ : Modelo MOSFET de señal pequeña

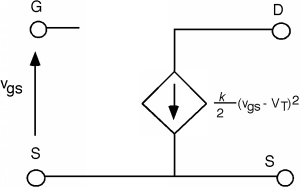
La puerta de un MOSFET tiene un voltaje V_gs relativo a la fuente. La conexión entre el drenaje y la fuente contiene una fuente de corriente que apunta hacia la fuente, con un valor igual a la mitad de k veces el cuadrado de la diferencia entre V_gs y V_T. — Figura $\PageIndex{3}$ : Modelo MOSFET de señal pequeña

Este parece ser un amplificador bastante bueno. Tiene impedancia de entrada infinita (y por lo tanto no cargará la etapa anterior del amplificador) y tiene una buena fuente de corriente controlada por voltaje (pero no lineal) para su salida. Una cifra en la sección sobre regímenes MOS muestra que a medida que $V_{\text{ds}}$ se incrementa, la longitud del canal, de hecho, se acorta un poco. El aumento $V_{\text{ds}}$ hace que la región de pellizco se expanda un poco, lo que, por supuesto, roba de la región del canal. Un canal más corto significa una resistencia de canal ligeramente menor, y así $I_{d}$ en realidad aumenta un poco con el aumento $V_{\text{ds}}$ en lugar de permanecer constante. Vimos desde el transistor bipolar, que cuando esto ocurre, debemos agregar una resistencia en paralelo con nuestra fuente de corriente. Así, completemos el modelo con un adicional $r_{o}$ pero de hecho, lo pondremos con una línea discontinua, ya que a excepción de los dispositivos de canal muy corto, tiene muy poco efecto en el rendimiento del dispositivo (Figura $\PageIndex{4}$ ).

Figura $\PageIndex{4}$ : Agregar un $r_{o}$

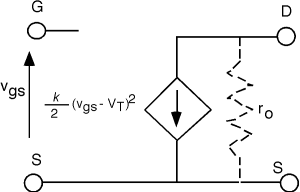
El modelo MOSFET de señal pequeña de la Figura 3 anterior, con la adición de una resistencia r_o que conecta el drenaje y la fuente, en paralelo con la fuente de corriente. — Figura $\PageIndex{4}$ : Agregar un $r_{o}$

El MOSFET tiene varias ventajas sobre el transistor bipolar. Una de las principales, como veremos, es que es mucho más fácil de hacer. Solo necesitas dos regiones n en un solo sustrato tipo p. Se trata básicamente de un dispositivo de superficie. Esto significa que no tienes que acumular diferentes capas de material tipo n y p como lo haces con el transistor bipolar. Por último, veremos que una variación en la tecnología MOSFET ofrece una gran ventaja sobre los dispositivos bipolares a la hora de construir circuitos lógicos con un gran número de puertas (circuitos VLSI y ULSI).

Para ver por qué esto es así, tenemos que desviarnos un poco, y discutir los circuitos lógicos.

Support Center

How can we help?