5.1: Introducción a las Líneas de Transmisión - Parámetros Distribuidos

Última actualización
Guardar como PDF

Page ID: 86507

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Habiendo aprendido algo sobre cómo generamos señales con transistores bipolares y de efecto de campo, ahora dirigimos nuestra atención al problema de obtener esas señales de un lugar a otro. Desde que Samuel Morse (y el fundador de mi alma mater, Ezra Cornell) demostraron el primer telégrafo en funcionamiento, ingenieros y científicos han estado trabajando en el problema de describir y predecir cómo se comportan las señales eléctricas a medida que viajan por estructuras específicas llamadas líneas de transmisión.

Cualquier estructura eléctrica que lleve una señal de un punto a otro puede considerarse una línea de transmisión. Ya sea un cable coaxial de larga distancia utilizado en Internet, un par trenzado en un edificio como parte de una red de área local, un cable que conecta una PC a una impresora, un diseño de bus en una placa base o una capa de metalización en un circuito integrado, el comportamiento fundamental de todas estas estructuras se describe por el mismo ecuaciones básicas. A medida que las velocidades de conmutación por computadora alcanzan los 100 megahercios, en el rango de gigahercios, las consideraciones sobre el comportamiento de la línea de transmisión son cada vez más críticas y se convierten en una fuerza más dominante en las limitaciones de rendimiento de cualquier sistema.

Para nuestros propósitos iniciales, presentaremos una figura de línea de transmisión “genérica”\(\PageIndex{1}\), que incorporará la mayoría (pero no todas) características de las líneas de transmisión reales. Luego haremos algunas simplificaciones bastante amplias, que, si bien hacen que nuestros resultados sean menos aplicables a situaciones de la vida real, simplifican enormemente las soluciones y nos llevan a ideas que, de hecho, podemos aplicar a una amplia gama de situaciones.

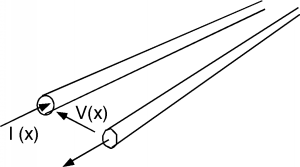Dos conductores cilíndricos paralelos se encuentran cerca uno del otro. Una corriente I (x) viaja por una de ellas, y regresa por la otra. Hay una diferencia de potencial de V (x) entre los conductores.

La línea genérica consta de dos conductores. Supondremos que\(V(x)\) existe una diferencia de potencial entre los dos conductores, y que una corriente\(I(x)\) fluye hacia abajo por un conductor, y regresa a través del otro. Por el momento, dejaremos que la línea de transmisión sea “semi-infinita”, lo que significa que tenemos acceso a la línea en algún momento\(x\), pero la línea luego se extiende en\(x\) dirección al infinito. (¡Tales líneas son un poco difíciles de manejar en el laboratorio!)

Para poder describir cómo\(V(x)\) y\(I(x)\) comportarse en esta línea, tenemos que hacer algún tipo de modelo de las características eléctricas de la propia línea. No podemos simplemente conformar cualquier modelo que queramos, sin embargo; tenemos que basar el modelo en realidades físicas.

Comencemos con solo considerar uno de los conductores y los efectos físicos de la corriente que fluye a través de ese conductor. Sabemos por la física de primer año que una corriente que fluye en un cable da lugar a un campo magnético,\(H\) (Figura\(\PageIndex{2}\)). Multiplica\(H\) por\(\mu\) y obtienes\(B\), la densidad del flujo magnético, y luego integra\(B\) sobre un plano paralelo a los cables y obtienes\(\Phi\), el flujo magnético que “une” el circuito. Esto se muestra en la Figura\(\PageIndex{3}\) para al menos parte de la superficie. La definición de\(L\), la inductancia de un elemento de circuito, es solo\[L = \frac{\Phi}{I}\]

donde\(\Phi\) está el flujo que une el elemento del circuito, y\(I\) es la corriente que fluye a través de él. Nuestro único problema al encontrar\(\Phi\) es que cuanto más larga sea una sección de alambre tomamos, más\(\Phi\) tenemos para lo mismo\(I\). Así, introduciremos el concepto de un parámetro distribuido.

Definición: Parámetro distribuido

Un parámetro distribuido es un parámetro que se extiende a lo largo de una estructura y no se limita a un elemento agrupado como una bobina de alambre.

Por ejemplo, definiremos aquí\(\mathbf{L}\) como la inductancia distribuida para la línea de transmisión. Cuenta con unidades de\(\mathrm{Henrys} / \mathrm{meter}\). Si tenemos una longitud de línea de transmisión\(x_{0}\) metros de largo, y si esa línea tiene una inductancia distribuida de\(\mathbf{L} \mathrm{~H} / \mathrm{m}\), entonces la inductancia\(L\) de esa longitud de línea es justa\(L = \mathbf{L} x_{0}\).

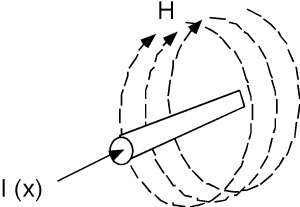Una corriente I (x) fluye hacia la página a lo largo de un conductor cilíndrico, generando un campo magnético H que gira en el sentido de las agujas del reloj.

De igual manera, si tenemos dos conductores separados por alguna distancia, y si hay una diferencia de potencial\(V\) entre los conductores, entonces debe haber alguna carga\(\pm (Q)\) en los dos conductores lo que da lugar a esa diferencia de potencial. Podemos imaginar una distribución lineal de carga en la línea de transmisión,\(\rho\) (en unidades de\(\mathrm{C} / \mathrm{m}\)), donde tenemos\(\rho \mathrm{~Coulombs} / \mathrm{m}\) en un conductor, y\(-\rho \mathrm{~Coulombs} / \mathrm{m}\) en el otro conductor. Para una línea de longitud\(x_{0}\), tendríamos\(Q = \pm \left(\rho x_{0}\right)\) en cada sección de alambre. Siempre que tenga dos conductores cargados con una diferencia de voltaje entre ellos, puede describir la relación entre la carga y el voltaje como una capacitancia. Los dos conductores tendrían una capacitancia\[\begin{array}{l} C &= \frac{Q}{V} \\ &= \frac{\rho x_{0}}{V} \end{array}\]

y una capacitancia distribuida\(\mathbf{C}\) (en unidades de\(\mathrm{Farads} / \mathrm{m}\)), que es justo\(\frac{\rho}{V}\). Una longitud de línea\(x_{0}\) larga tendría una capacitancia\(C = \mathbf{C} x_{0} \mathrm{~Farads}\) asociada a ella, como en la Figura\(\PageIndex{4}\).

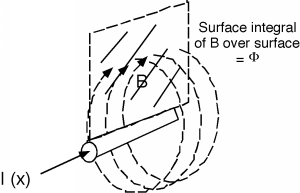El conductor y el campo magnético de la Figura 2 anterior se muestran, con B, la densidad de flujo magnético, estando integrada sobre la superficie de un plano vertical que discurre paralelo al conductor para obtener Phi.

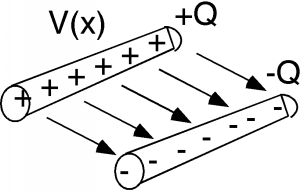Dos cables paralelos, con el de la izquierda llevando una carga positiva Q y el de la derecha llevando una carga negativa -Q. El cable de la izquierda tiene un potencial V (x) en relación con el cable de la derecha.

Así, vemos que la línea de transmisión tiene tanto una inductancia\(\mathbf{L}\) distribuida como una capacitancia distribuida\(\mathbf{C}\), las cuales están atadas entre sí. Realmente no hay manera de que podamos separar uno del otro. En otras palabras, no podemos tener sólo la capacitancia, o solo la inductancia'; siempre habrá algo de cada uno asociado a cada sección de línea ahora importa cuán pequeña o cuán grande la hagamos.

Ya estamos listos para construir nuestro modelo. Lo que queremos hacer es llegar a alguna disposición de inductores y capacitores que representen eléctricamente las propiedades de la capacitancia distribuida y la inductancia que discutimos anteriormente. A medida que un largo de línea se alarga, su capacitancia aumenta, así que mejor tendríamos que poner las capacitancias distribuidas en paralelo entre sí, ya que esa es la forma en que se suman los condensadores. También, a medida que la línea se alarga, su inductancia total aumenta, así que mejor teníamos que poner las inductancias distribuidas en serie entre sí, pues esa es la forma en que se suman las inductancias. La figura\(\PageIndex{5}\) es una representación de la inductancia y capacitancia distribuidas de la línea de transmisión genérica.

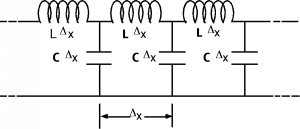Un cable horizontal contiene tres inductores cuya inductancia es el producto de la inductancia unitaria y Delta x. A la derecha de cada inductor, un cable vertical que contiene un condensador cuya capacitancia es el producto de la capacitancia de la unidad y Delta x conduce hacia abajo a un cable horizontal inferior que no contiene elementos. La distancia entre los cables verticales adyacentes es Delta x Este patrón continúa hacia la izquierda y la derecha de la sección mostrada.

Rompemos la línea en secciones\(\Delta x\) largas, cada una con una inductancia\(\mathbf{L} \Delta x\) y una capacitancia\(\mathbf{C} \Delta x\). Si reducimos a la mitad\(\Delta x\), reduciríamos a la mitad la inductancia y capacitancia de cada sección, pero tendríamos el doble de ellas por unidad de longitud. ¡Duh! El punto es que no importa lo finos que hagamos\(\mathbf{C} \Delta x\), todavía tenemos inductores y capacitores dispuestos como vemos en la Figura\(\PageIndex{5}\), con los dos tipos de componentes entremezclados.

Podríamos hacer un modelo más realista y darnos cuenta de que todos los cables reales tienen resistencia en serie asociada a ellos, y que lo que sea que usemos para mantener los dos conductores separados tendrá alguna conductancia de fuga asociada. Para dar cuenta de esto, introduciríamos una resistencia en serie\(\mathbf{R}\) (\(\Omega\)por unidad de longitud) y una conductancia en serie\(\mathbf{G}\) (\(\Omega\)por unidad de longitud). Una sección de nuestro modelo de línea entonces se parece a Figura\(\PageIndex{6}\).

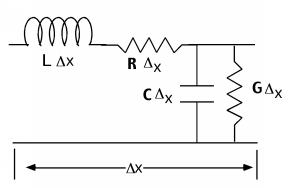Una sección de longitud Delta x de dos alambres horizontales. El cable superior conecta un inductor y una resistencia en serie. Dos cables verticales, uno que contiene un condensador y el otro que contiene una derivación, conectan los cables horizontales entre sí. Los valores de la inductancia, resistencia, capacitancia y conductancia de los componentes son los productos de los respectivos valores unitarios y la longitud de sección Delta x.

A pesar de que se trata de un modelo más realista, lleva a matemáticas mucho más complicadas. Empezaremos de todos modos, ignorando la resistencia en serie\(\mathbf{R}\) y la conductancia de derivación\(\mathbf{G}\). Esta “aproximación” resulta ser bastante buena siempre y cuando o la línea no sea demasiado larga, o las frecuencias de las señales que estamos enviando por la línea no lleguen demasiado altas. Sin la resistencia en serie o la conductancia paralela tenemos lo que se llama una línea de transmisión ideal sin pérdidas.