5.8: Líneas en cascada
- Page ID
- 86508
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)También podemos usar diagramas de rebote para manejar problemas algo más complicados.
Arnold Aggie decide agregar una interfaz ethernet adicional a la que ya está conectada a su computadora. Decide simplemente agregar una “T” al terminal donde el cable está conectado a su interfaz de “red delgada”, y agregar un poco más de cable. Desafortunadamente, no tiene cuidado con el cable coaxial que usa, por lo que tiene algo de\(75 \mathrm{~ \Omega}\) televisión co-ax en lugar del cable\(50 \mathrm{~ \Omega}\) ethernet. Termina con la situación que se muestra en la Figura\(\PageIndex{1}\). Este tipo de problema se llama problema de línea en cascada porque tenemos dos líneas diferentes, una enganchada tras otra. El análisis es similar a lo que hemos hecho antes, solo un poco más complicado es todo.
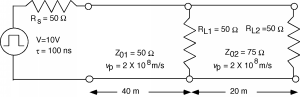 Figura\(\PageIndex{1}\): Problema de línea en cascada
Figura\(\PageIndex{1}\): Problema de línea en cascada

Tendremos que pensar un poco más antes de poder dibujar el diagrama de rebote para este problema. El controlador para cable ethernet que llega a la computadora de Arnold se puede modelar como\(10 \mathrm{~V}\) (open circuit) source with a \(50 \mathrm{~\Omega}\) internal impedance. Since the source does not (initially) know anything about how the line it is driving is terminated, the first signal \(V_{1}^{+}\) will be the same as in our initial problem, in this case just a +\(5 \mathrm{~V}\) signal headed down the line.
Let's focus on the "T" for a minute, as shown in Figure \(\PageIndex{2}\).
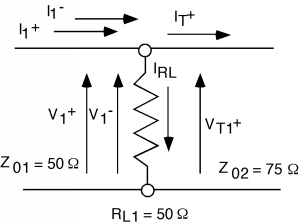 Figure \(\PageIndex{2}\): At the junction
Figure \(\PageIndex{2}\): At the junction

\(V_{1}^{+}\)es incidente en el cruce. Cuando choca con el cruce, habrá una onda reflejada\(V_{1}^{-}\) y también ahora una onda transmitida\(V_{T1}^{+}\). Dado que la onda incidente no puede decir la diferencia entre una\(75 \mathrm{~\Omega}\) resistencia y una línea de\(75 \mathrm{~\Omega}\) transmisión, piensa que está viendo una resistencia de terminación igual a una\(50 \mathrm{~\Omega}\) resistencia (\(R_{L1}\)) en paralelo con una\(75 \mathrm{~\Omega}\) resistencia (la segunda línea). \(50 \mathrm{~\Omega}\)en paralelo con\(75 \mathrm{~\Omega}\) is\(30 \mathrm{~\Omega}\). Llamemos a esta resistencia de carga “aparente”\(R'_{L}\), para que luego podamos calcular\(\Gamma_{V_{12}}\), el primer coeficiente de reflexión de voltaje al pasar de la línea 1 a la línea 2 como:\[\begin{array}{l} \Gamma_{V_{12}} &=& \dfrac{R'_{L} - Z_{01}}{R'_{L} + Z_{01}} \\[4pt] &=& \dfrac{30 - 50}{30 + 50} \\ &=& -0.25 \end{array}\]
Tenga en cuenta que podríamos haber comenzado desde cero y anotado KVL y KCL para el cruce\[V_{1}^{+} + V_{1}^{-} = V_{T1}^{+}\]
y\[I_{1}^{+} + I_{1}^{-} = I_{RL} + I_{T1}^{+}\]
Luego, reescribiendo Ecuación\(\PageIndex{3}\) en términos de voltaje e impedancias tenemos:\[\frac{V_{1}^{+}}{Z_{01}} - \frac{V_{1}^{-}}{Z_{01}} = \frac{V_{T1}^{+}}{Z_{02}} + \frac{V_{T1}^{+}}{R_{L}}\]
Ahora tenemos dos ecuaciones con dos incógnitas (\(V_{1}^{+}\)y\(V_{T1}^{+}\)). Al resolver Ecuación\(\PageIndex{4}\) para\(V_{T1}^{+}\) y luego enchufarlo a Ecuación\(\PageIndex{2}\), podríamos obtener la relación de\(V_{1}^{-}\) a\(V_{1}^{+}\), o el coeficiente de reflexión de voltaje. El lector interesado puede confirmar que efectivamente, obtienes el mismo resultado de esta manera.
Para poder resolver completamente este problema, también necesitamos saber\(V_{T1}^{+}\), la onda transmitida también. Dado que la ecuación\(\PageIndex{2}\) dice\(V_{T1}^{+}\) es solo la suma del incidente y las ondas reflejadas en la primera línea\[V_{T1}^{+} = V_{1}^{+} + \Gamma_{V_{12}} V_{1}^{+}\]
Así podemos escribir\[\frac{V_{T1}^{+}}{V_{L}^{+}} = 1 + \Gamma_{V_{12}} = \frac{R'_{L} + Z_{01}}{R'_{L} + Z_{01}} + \frac{R'_{L} - Z_{01}}{R'_{L} + Z_{01}} = \frac{2 R'_{L}}{R'_{L} + Z_{01}} = \frac{60}{30 + 50} = 0.75 \equiv T_{V_{12}}\]
Una cosa importante a tener en cuenta es que\[T_{V} = 1 + \Gamma_{V}\] NO\[T_{V} + \Gamma_{V} = 1\]
No “conservamos” voltaje en una terminación, en el sentido de que el voltaje reflejado y transmitido tiene que sumar para ser el voltaje incidente. Más bien, el voltaje transmitido es la suma del voltaje incidente y el voltaje reflejado, para que podamos obedecer la ley de voltaje de Kirchoff.
Ahora podemos comenzar a hacer nuestro diagrama de rebote. Propagamos una\(+5 \mathrm{~V}\) onda y una\(-5 \mathrm{~V}\) onda (separada por\(100 \mathrm{~ns}\)) hacia abajo hacia el cruce. Dado que la línea es\(40 \mathrm{~m}\) larga, y las olas se mueven en\(2 \times 10^{8} \ \frac{\mathrm{m}}{\mathrm{s}}\), se necesita\(200 \mathrm{~ns}\) para que lleguen al cruce. Allí, una\(-1.25 \mathrm{~V}\) onda se refleja de nuevo hacia la fuente, y una\(+3.75 \mathrm{~V}\) onda se transmite a la segunda línea de transmisión en la Figura\(\PageIndex{3}\).
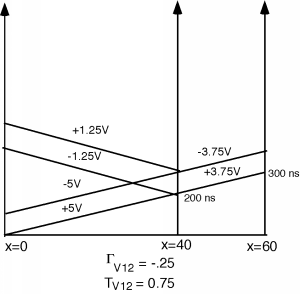
Figura\(\PageIndex{3}\): Reflexión y transmisión en la “T”

Dado que la carga para la segunda línea es\(50 \mathrm{~\Omega}\), and the characteristic impedance, \(Z_{02}\), for the second line is \(75 \mathrm{~\Omega}\), we will have a reflection coefficient, \[\begin{array}{l} \Gamma_{V_{2}} &=& \dfrac{R_{L2} - Z_{02}}{R_{L2} + Z_{02}} \\[4pt] &=& \dfrac{50 - 75}{50 + 75} \\ &=& -0.2 \end{array}\]
Thus a \(-0.75 \mathrm{~V}\) signal is reflected off of the second load in Figure \(\PageIndex{4}\).
What is the magnitude of the voltage which is developed across the second load?
- Answer
-
3 Volts!
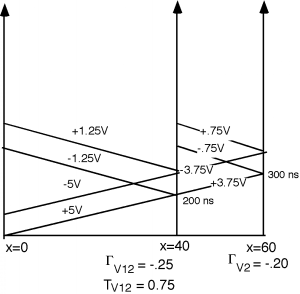 Figure \(\PageIndex{4}\): Reflection of transmitted pulse
Figure \(\PageIndex{4}\): Reflection of transmitted pulse

¿Qué pasa con el\(0.75 \mathrm{~V}\) pulso cuando llega a la “T”? Bueno, aquí hay otro desajuste, con un coeficiente de reflexión\(\Gamma_{V_{21}}\) dado por\[\begin{array}{l} \Gamma_{V_{21}} &=& \dfrac{25 - 75}{25 + 75} \\ &=& -0.5 \end{array}\]
(La\(50 \mathrm{~V}\) resistencia y la línea de\(50 \mathrm{~V}\) transmisión parecen una\(25 \mathrm{~\Omega}\) terminación para\(75 \mathrm{~\Omega}\)línea) y un coeficiente de transmisión\[\begin{array}{l} T_{V_{21}} &=& 1 + \Gamma_{V_{21}} \\ &=& 0.5 \end{array}\]
y así agregamos al diagrama de rebote en la Figura\(\PageIndex{5}\).
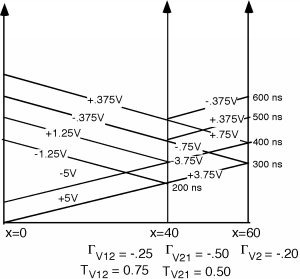 Figura\(\PageIndex{5}\): Cuando el pulso de carga reflejado golpea la unión
Figura\(\PageIndex{5}\): Cuando el pulso de carga reflejado golpea la unión

Podríamos seguir adelante, pero el voltaje reflejado de la segunda carga solo será\(75 \mathrm{~mV}\) now, so let's call it a day.
There are a couple of other interesting applications of bounce diagrams and the transient behavior of transmission lines that we might look at before we move on to other things. The first is called the Charged Line Problem. Here it is:
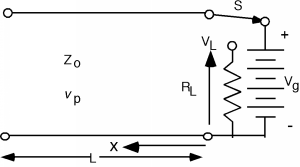 Figure \(\PageIndex{6}\): The "Charged Line" problem
Figure \(\PageIndex{6}\): The "Charged Line" problem

Contamos con una línea de transmisión con impedancia característica\(Z_{0}\) y velocidad de fase\(v_{p}\). Es\(L\) largo, y desde hace algún tiempo se ha conectado a una batería de potencial\(V_{g}\) como se muestra en la Figura\(\PageIndex{7}\). En el momento\(t=0\),\(S\) se lanza el interruptor, que retira la batería del circuito, y conecta la línea a una resistencia de carga\(R_{L}\). La pregunta es: ¿cómo se ve el voltaje a través de la resistencia de carga\(V_{L}\),, en función del tiempo? Esto es casi como lo que hemos hecho antes, pero no del todo.
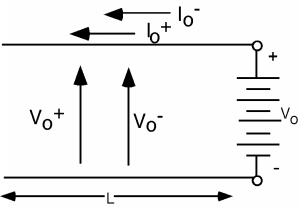 Figura\(\PageIndex{7}\): Condiciones iniciales
Figura\(\PageIndex{7}\): Condiciones iniciales

En primer lugar, ahora tenemos condiciones iniciales distintas de cero. Para\(t=0\) we will have both voltages and current on the line. In order to match boundary conditions, we must do more than have one voltage and one current, because the voltage on the line must be \(V_{g}\), while the current flowing down the line must be \(0\). So, we will put in both a \(V^{+}\) and a \(V^{-}\) and their corresponding currents. Note that \(x\) is going to the left this time. Let's forget about the switch and the load resistor for a minute and just look at the line and battery. We have two equations we must satisfy: \[V_{0}^{+} + V_{0}^{-} = V_{g}\] and \[I_{0}^{+} + I_{0}^{-} = 0\]
We can use the impedance relationship to change Equation \(\PageIndex{13}\) to: \[\frac{V_{0}^{+}}{Z_{0}} - \frac{V_{0}^{-}}{Z_{0}} = 0\]
I hope most of you can then see by inspection that we must have \[\begin{array}{l} V_{0}^{+} &=& V_{0}^{-} \\[4pt] &=& \dfrac{V_{g}}{2} \end{array}\]
OK, the switch \(S\) is thrown at \(t=0\). Now the end of the line looks like Figure \(\PageIndex{8}\).
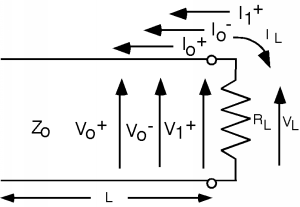
Figure \(\PageIndex{8}\): After the Resistor is Connected

Hemos anticipado el hecho de que vamos a necesitar otra onda de voltaje y corriente si vamos a poder igualar las condiciones límite cuando la resistencia de carga está conectada, y hemos agregado a\(V_{1}^{+}\) y\(V_{1}^{-}\) a la línea. Estas son nuevas ondas de voltaje y corriente que se originan en la posición de resistencia de carga para satisfacer las nuevas condiciones de límite allí. Ahora volvemos a hacer KVL y KCL. \[V_{0}^{+} + V_{0}^{-} + V_{1}^{+} = V_{L}\]y\[\frac{V_{0}^{+}}{Z_{0}} - \frac{V_{0}^{-}}{Z_{0}} + \frac{V_{1}^{+}}{Z_{0}} = - \frac{V_{L}}{R_{L}}\]
Ya hemos hecho la sustitución de impedancia para la ecuación actual en Ecuación\(\PageIndex{17}\). Sabemos cuál es la suma y la diferencia de\(V_{0}^{+}\) y\(V_{0}^{-}\) son, así que vamos a sustituirlos en. \[V_{g} + V_{1}^{+} = V_{L}\]y\[\frac{V_{1}^{+}}{Z_{0}} = - \frac{V_{L}}{R_{L}}\]
De esto obtenemos\[V_{L} = -\left( \frac{R_{L}}{Z_{0}} V_{1}^{+}\right)\]
que sustituimos de nuevo en Ecuación\(\PageIndex{18}\):\[V_{g} + V_{1}^{+} = -\left( \frac{R_{L}}{Z_{0}} V_{1}^{+}\right)\]
Entonces podemos resolver para\(V_{1}^{+}\):\[\begin{array}{l} V_{1}^{+} &=& -\dfrac{V_{g}}{1 + \frac{R_{L}}{Z_{0}}} \\[4pt] &=& -\left( \dfrac{Z_{0}}{R_{L} + Z_{0}} V_{g}\right) \end{array}\]
El voltaje en la carga viene dado por Ecuación\(\PageIndex{18}\) y es claramente justo:\[V_{L} = V_{g} - \frac{Z_{0}}{R_{L} + Z_{0}} V_{g}\]
y en particular, cuando\(R_{L}\) se elige para ser\(Z_{0}\) (lo cual se suele hacer cuando se utiliza este circuito), tenemos\[V_{L} = \frac{V_{g}}{2}\]
Ahora, ¿qué hacemos? ¡Construimos un diagrama de rebote! Quedémonos con la suposición de que\(R_{L} = Z_{0}\), en cuyo caso el coeficiente de reflexión en el extremo de la resistencia es\(0\). En el extremo de circuito abierto de la línea de transmisión\(\Gamma\) es\(+1\). Entonces tenemos Figura\(\PageIndex{9}\).
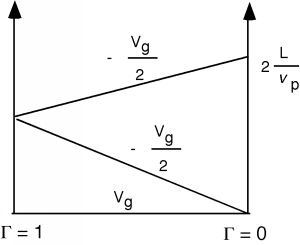 Figura\(\PageIndex{9}\): Diagrama de rebote para el problema de la línea cargada
Figura\(\PageIndex{9}\): Diagrama de rebote para el problema de la línea cargada

Tenga en cuenta que para este diagrama de rebote, hemos agregado un voltaje adicional,\(V_{g}\), on the baseline to indicate that there is an initial voltage on the line, before the switch is thrown, and \(t\) starts on the bounce diagram.
If we concentrate on the voltage across the load, we add \(V_{g}\) and \(-\frac{V_{g}}{2}\) and find that the voltage across the load resistor rises to \(\frac{V_{g}}{2}\) at time \(t=0\) in Figure \(\PageIndex{10}\). The \(-\frac{V_{g}}{2}\) voltage wave travels down the line, hits the open circuit, reflects back, and when it gets to the load resistor, brings the voltage across the load resistor back down to zero. We have made a pulse generator!
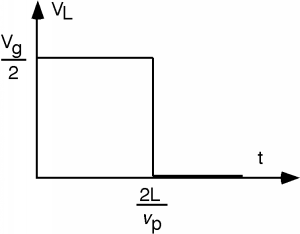 Figure \(\PageIndex{10}\): Voltage \(V_{L}\) across the load resistor \(R_{L}\)
Figure \(\PageIndex{10}\): Voltage \(V_{L}\) across the load resistor \(R_{L}\)

En la era digital actual, esto podría parecer una forma extraña de crear un pulso. Imagínese, sin embargo, si necesitara un pulso con un potencial muy grande (cientos de miles o incluso millones de voltios) para, digamos, un acelerador de partículas. ¡Es poco probable que alguna vez se construya un MOSFET que está a la altura de la tarea! De hecho, en un campo de estudio llamado electrónica de potencia pulsada solo esos circuitos se utilizan todo el tiempo. A veces se construyen con líneas de transmisión reales, a veces se construyen a partir de inductores y capacitores discretos, enganchados juntos al igual que en el modelo de parámetros distribuidos. Dichos circuitos se denominan redes de formación de pulsos o PFN para abreviar.
Por último, solo porque nos brinda una buena oportunidad para revisar cómo llegamos a donde estamos ahora mismo, consideremos el problema de una carga no resistiva al final de una línea. ¡Supongamos que la línea termina con un condensador! Por simplicidad, vamos a dejar\(R_{s} = Z_{0}\), así que cuando se cierra el interruptor una onda\(S\) se\(V_{1}^{+} = \frac{V_{g}}{2}\) dirige hacia abajo de la línea como en la Figura\(\PageIndex{11}\). Pensemos en lo que sucede cuando golpea el condensador. Sabemos que necesitamos generar una señal reflejada\(V_{1}^{-}\), así que sigamos adelante y pongamos esto en Figura\(\PageIndex{12}\), junto con su onda de corriente complementaria.
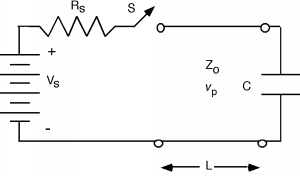 Figura\(\PageIndex{11}\): Problema transitorio con carga capacitiva
Figura\(\PageIndex{11}\): Problema transitorio con carga capacitiva

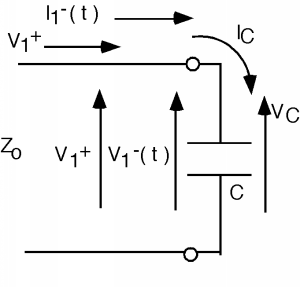 Figura\(\PageIndex{12}\): El pulso inicial golpea la carga
Figura\(\PageIndex{12}\): El pulso inicial golpea la carga

El condensador está inicialmente descargado, y sabemos que no podemos cambiar instantáneamente el voltaje a través de un condensador (¡al menos sin una corriente infinita!) y así el voltaje inicial a través del condensador debe ser cero, haciendo\(V_{1}^{-} (0) = -V_{1}^{+}\), if we make time \(t=0\) be when the initial wave just gets to the capacitor. So, at \(t=0\), \(\Gamma_{V}(0) = -1\). Note that we are making \(\Gamma\) a function of time now, as it will change depending upon the charge state of the capacitor.
The current into the capacitor, \(I_{C}\), is just \(I_{1}^{+} - I_{1}^{-}(t)\). \[\begin{array}{l} I_{C}(0) &=& I_{1}^{+} + I_{1}^{-}(0) \\[4pt] &=& \dfrac{V_{g}}{Z_{0}} \end{array}\] since \[\begin{array}{l} I_{1}^{+} &=& \dfrac{V_{1}^{+}}{Z_{0}} \\[4pt] &=& \dfrac{V_{g}}{2 Z_{0}} \end{array}\] and \[\begin{array}{l} I_{1}^{-} (0) &=& -\dfrac{V_{1}}{Z_{0}} \\[4pt] &=& \dfrac{V_{g}}{2 Z_{0}} \end{array}\]
How will the current into the capacitor, \(I_{C}(t)\), behave? We have to remember the capacitor equation: \[\begin{array}{l} I_{C} (t) &=& C \dfrac{\text{d} V_{C}(t)}{\text{d} t} \\[4pt] &=& C \left(\dfrac{\partial \left(V_{1}^{+} + V_{1}^{-}(t)\right)}{\partial t}\right) \\[4pt] &=& C \dfrac{\text{d} V_{1}^{-}(t)}{\text{d} t} \end{array}\] since \(V_{1}^{+}\) is a constant and hence has a zero time derivative. Well, we also know that \[\begin{array}{l} I_{C}(t) &=& I_{1}^{+} + I_{1}^{-}(t) \\[4pt] &=& \dfrac{V_{1}^{+}}{Z_{0}} - \dfrac{V_{1}^{-} (t)}{Z_{0}} \end{array}\]
So we equate Equations \(\PageIndex{28}\) and \(\PageIndex{29}\) and we get \[C \frac{\text{d} V_{1}^{-}(t)}{\text{d} t} = \frac{V_{1}^{+}}{Z_{0}} - \frac{V_{1}^{-} (t)}{Z_{0}}\]
or \[\frac{\text{d} V_{1}^{-} (t)}{\text{d} t} + \frac{1}{Z_{0} C} V_{1}^{-} (t) = \frac{1}{C} \frac{V_{1}^{+}}{Z_{0}}\]
which gets us back to another differential equation!
The homogeneous solution is easy. We have \[\frac{\text{d} V_{1}^{-} (t)}{\text{d} t} + \frac{1}{Z_{0} C} V_{1}^{-} (t) = 0\]
for which the solution is obviously \[V_{1, \text{homo}}^{-} (t) = V_{0} e^{-\frac{t}{Z_{0} C}}\]
After a long time, the derivative of the homogeneous solution is zero, and so the particular solution (the constant part) is the solution to \[\frac{1}{Z_{0} C} V_{1, \text{part}}^{-} = \frac{1}{C} \frac{V_{1}^{+}}{Z_{0}}\] or \[V_{1, \text{part}}^{-} = V_{1}^{+}\]
The complete solution is the sum of the two: \[\begin{array}{l} V_{1}^{-}(t) &=& V_{1, \text{homo}}^{-} (t) + V_{1, \text{part}}^{-} \\ &=& V_{0} e^{-\frac{t}{Z_{0} C}} + V_{1}^{+} \end{array}\]
Now all we need to do is find \(V_{0}\), the initial condition. We know, however, that \(V_{1}^{-} (0) = -V_{1}^{+}\), so that makes \(V_{0} = -2 V_{1}^{+}\)! So we have: \[\begin{array}{l} V_{1}^{-} (t) &=& 2 V_{1}^{+} e^{- \frac{t}{Z_{0} C}} + V_{1}^{+} \\ &=& V_{1}^{+} \left(1 - 2e^{- \frac{t}{Z_{0} C}}\right) \end{array}\]
Since \(V_{1}^{+} = \frac{V_{g}}{2}\), we can plot \(V_{1}^{-} (t)\) as a function of time from which we can make a plot of \(\Gamma_{V} (t)\):
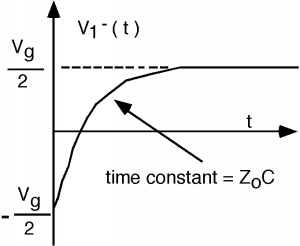 Figure \(\PageIndex{13}\): Reflected voltage as a function of time
Figure \(\PageIndex{13}\): Reflected voltage as a function of time

El condensador comienza pareciendo un cortocircuito, y se carga para parecer un circuito abierto, lo cual tiene perfecto sentido. ¿Se puede averiguar cuál sería la forma de un pulso reflejado en el condensador, dado que la constante de tiempo\(Z_{0} C\) era corta comparada con el ancho del pulso?


