6.2: Comportamiento de la línea del A/C

Última actualización
Guardar como PDF

Page ID: 86565

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Si vamos a tratar de usar fasores en una línea de transmisión, entonces también tenemos que permitir la variación espacial. Esto es sencillo de hacer, si solo dejamos que el fasor sea una función de$x$, así lo hemos hecho$\widetilde{V} (x)$. Cómo varía el fasor$x$ es una de las cosas que ahora tenemos que averiguar.

Empecemos de nuevo con las Ecuaciones del Telégrafo. \[\frac{\partial V(x, t)}{\partial x} = (- \mathbf{L}) \frac{\partial I(x, t)}{\partial t}\]\[\frac{\partial I(x, t)}{\partial x} = (- \mathbf{C}) \frac{\partial V(x, t)}{\partial t}\]

Porque ahora$V(x, t)$ podemos sustituir$\widetilde{V} (x) e^{i \omega t}$ y para$I(x, t)$ enchufamos$\widetilde{I} (x) e^{i \omega t}$. Entonces obtenemos:\[\frac{\partial \left( \widetilde{V}(x) e^{i \omega t} \right)}{\partial x} = (- \mathbf{L}) \frac{\partial \left( \widetilde{I}(x) e^{i \omega t} \right)}{\partial t}\]

y\[\frac{\partial \left(\widetilde{I}(x) e^{i \omega t} \right)}{\partial x} = (- \mathbf{C}) \frac{\partial \left(\widetilde{V}(x) e^{i \omega t} \right)}{\partial t}\]

Tomamos la derivada con respecto al tiempo, que baja una$i \omega$, y luego cancelamos la$i \omega$ de ambos lados de cada ecuación:\[\frac{\partial \widetilde{V}(x)}{\partial x} = -\left(i \omega \mathbf{L} \widetilde{I}(x) \right)\]

y\[\frac{\partial \widetilde{I}(x)}{\partial x} = -\left(i \omega \mathbf{C} \tilde{V}(x) \right)\]

¡Voila! En un simple movimiento, ¡hemos eliminado por completo la variable de tiempo,$t$, de nuestras ecuaciones! Realmente no se ha ido, claro, por una vez averiguamos qué$\widetilde{V} (x)$ es, tenemos que multiplicarlo por$e^{i \omega t}$ y luego tomar la parte real antes de poder extraer, una vez más, lo real$V(x, t)$ que queremos. No obstante, en lo que respecta a las ecuaciones del telégrafo,$t$ ha desaparecido de la pantalla del radar.

Para resolverlos hacemos justo lo que hicimos con el problema transitorio. Tomamos una derivada con respecto a$x$ de la Ecuación$\PageIndex{5}$, que nos da una$\frac{\partial \widetilde{I} (x)}{\partial x}$ en el lado derecho, por la cual podemos sustituir Ecuación$\PageIndex{6}$, que nos deja con\[\frac{\partial^{2} \widetilde{V} (x)}{\partial x^{2}} = - \left(\omega^{2} \mathbf{LC} \widetilde{V} (x)\right)\]

($-$tiempos$-$ es$+$, pero$ii = -1$ y así tenemos un$-$ frente a la$\omega^{2}$). Luego reescribimos la ecuación$\PageIndex{7}$ como\[\frac{\partial^{2} \widetilde{V} (x)}{\partial x^{2}} + \omega^{2} \mathbf{LC} \widetilde{V} (x) = 0\]

La solución más simple a esta ecuación es\[\widetilde{V} (x) = V_{0} e^{\pm \left(i \omega \sqrt{\mathbf{LC}} x \right)}\]

de la que luego podemos obtener la señal de voltaje real\[\begin{array}{l} V(x, t) &=& \widetilde{V}(x) e^{i \omega t} \\[4pt] &=& V_{0} e^{i \left(\omega t \pm \omega \sqrt{\mathbf{LC}} x \right)} \end{array}\]

Tenga en cuenta que podríamos facturar un$e^{i \omega \sqrt{\mathbf{LC}}}$ desde el exponente, que, como es solo una constante, podríamos incluirlo en$V_{0}$ (y llamarlo$V_{0}'$), cambiar el orden de$x$ y$t$, y escribir Ecuación$\PageIndex{10}$ como\[V(x, t) = V_{0}' e^{i \left(x \pm \frac{1}{\sqrt{\mathbf{LC}}} t \right)}\]

¡que se parece mucho a la$f(x \pm vt)$ solución “general” de la que estábamos hablando antes!

El número$\omega \sqrt{\mathbf{LC}}$ es especial. Por lo general, se representa con la letra griega$\beta$ y se llama el coeficiente de propagación. Así tenemos\[V(x, t) = V_{0} e^{i \left(\omega t \pm \beta x\right)}\]

Como antes, un punto en la onda de fase constante requiere que el argumento dentro del paréntesis permanezca constante. Así, si$V(x_{1}, t_{1})$ va a igualar$V(x_{2}, t_{2})$ (es decir, lo que estaba$x_{1}$ en el punto$t_{1}$ es ahora$x_{2}$ en el momento$t_{2}$), debe ser que\[\omega t_{1} \pm \beta x_{1} = \omega t_{2} \pm \beta x_{2}\]

\frac{x_{2} - x_{1}}{t_{2} - t_{1}} = \frac{Δ}{(x)} = \pm (\frac{ω}{β}) = \pm (\frac{ω}{ω}) = \pm (\frac{1}{\sqrt{L C}}) \equiv v_{p}

Cuál de nuevo, define la velocidad de fase de la onda. Otras relaciones a tener en cuenta son

β = \frac{2}{π}

\begin{array}{rcl} λ & = & \frac{v_{p}}{f} \\ = & \frac{\frac{ω}{β}}{\frac{ω}{2}} \\ = & \frac{2}{π} \end{array}

El primero viene del hecho de que la ola varía en $x$ como $e^{i β x}$ . Por lo tanto, cuando $x = γ$ , la longitud de onda, $β γ$ solo aumenta en $2 π$ , para conseguir que el fasor pase por una rotación completa. Obsérvese también, como antes, la elección del signo menos en el ± en Ecuación representa una onda que va en el $x$ dirección, mientras que la elección del signo + dará una ola que va en el $- x$ dirección. Claramente, al comenzar tomando la derivada x de la ecuación para $I (x, t)$ terminaríamos con

I (x, t) = I_{0} e^{i (ω t \pm β x)}

Consideremos entonces los dos fasores y definamos el fasor de voltaje asociado con la onda de voltaje positiva como

{\tilde{V}}_{más} (x) = V^{+} e^{- (i β x)}

y el fasor de voltaje negativo como

{\tilde{V}}_{menos} (x) = V^{-} e^{i β x}

Debemos tener en cuenta que tanto $V^{+}$ y $V^{-}$ pueden ser, y probablemente son, números complejos. (A partir de ahora dejaremos caer el pequeño ~ sobre las variables porque es muy tedioso conseguir que aparezca con este procesador de textos. Solo tendrás que tener en cuenta que cualquier variable que no pongamos explícitamente dentro de los marcadores de valor absoluto (i.e. $| V^{+} |$ ) va a ser, en general, un número complejo). Tendremos, por supuesto, expresiones similares para las ondas de corriente que van positivas y negativas.

Consideremos las ondas positivas de corriente y voltaje, y conectémoslas a la Ecuación.

\frac{\partial^{} (V^{+} e^{- (i β x)})}{\partial x^{}} = - (i ω L I^{+} e^{- (i β x)})

La derivada x trae abajo un $- (i β)$ , el $e^{- (i β x)}$ de cancelar, y tenemos

V^{+} = \frac{i ω L}{i β} I^{+}

Pero, desde $β = ω \sqrt{L C}$ tenemos

V^{+} = \sqrt{\frac{L}{C}} I^{+} \equiv Z_{0} I^{+}

como lo habíamos hecho antes.

Entonces, ¿qué ha cambiado? No mucho del caso de los transitorios en una línea. Ahora vamos a suponer que tenemos un problema de estado estacionario. Esto significa que encendimos el generador hace mucho tiempo. Suponemos que ha estado conectado a la línea el tiempo suficiente para que todo el comportamiento transitorio se haya extinguido, y que los voltajes y corrientes ya no están cambiando (excepto oscilando en frecuencia $ω$ , por supuesto).

Si la línea es semi-infinita (o coincide con una carga igual a $Z_{0}$ ) como en Figura$\PageIndex{1}$ entonces es bastante obvio que

V^{+} = \frac{Z_{0}}{Z_{0} + Z_{g}} V_{g}

donde $Z_{g}$ es la impedancia de la fuente, y $V_{g}$ es el fasor de voltaje de la fuente.

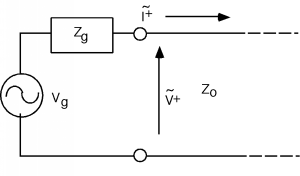
Una línea de transmisión con impedancia Z_0 y longitud infinita está unida en su extremo izquierdo a una fuente de voltaje sinusoidal v_g con una impedancia de fuente z_g El voltaje desde el extremo inferior al extremo superior izquierdo de la línea de transmisión es tilde V+, y la corriente que ingresa a la línea de transmisión, moviéndose hacia la derecha, es tilde I+.