6.5: Diagrama de manivela

De hecho todavía tenemos algunas opciones abiertas para nosotros. Uno de los más agradables, al menos en términos de obtener alguna idea, se llama diagrama de manivela. Tenga en cuenta que esta ecuación es una ecuación compleja, la cual nos obliga a tomar la relación de dos números complejos:$1+{\Gamma }_{\nu }{e}^{-(i2\beta s)}$y$1-{\Gamma }_{\nu }{e}^{-(i2\beta s)}$.

Trazemos estas dos cantidades en el plano complejo, comenzando en$s=0$(el extremo de carga de la línea). Podemos representar${\Gamma }_{\nu }$, el coeficiente de reflexión, por su magnitud y su fase, que son$\left|{\Gamma }_{\nu }\right|$y${\phi }_{\Gamma }$. Para el numerador trazamos un 1, y luego agregamos el vector complejo$\Gamma$que tiene una longitud$\left|\Gamma \right|$y se sienta en ángulo${\phi }_{\Gamma }$con respecto al eje real, como se muestra en la Figura\(\PageIndex{1}\). El denominador es exactamente lo mismo, excepto que el\(\Gamma\) vector apunta en dirección opuesta como se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{1}\): Plotting $1+{\Gamma }_{\nu }$

Figura\(\PageIndex{2}\): Trazado$1-{\Gamma }_{\nu }$

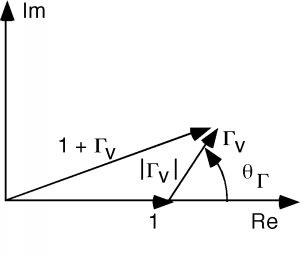
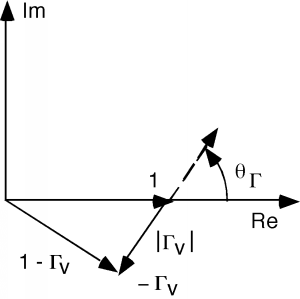
El vector superior es proporcional a$V\left(s\right)$y el vector inferior es proporcional a$I\left(s\right)$Figura\(\PageIndex{3}\). Por supuesto, para$s=0$estamos a la carga, así que$V\left(s=0\right)=V_L$y$I\left(s=0\right)=I_L$.

Figura\(\PageIndex{3}\): Another crank diagram showing that $1+{\Gamma }_{\nu }=\frac{V_L}{V^{+}}$ and $1-{\Gamma }_{\nu }=\frac{Z_0{I}_L}{V^{+}}$

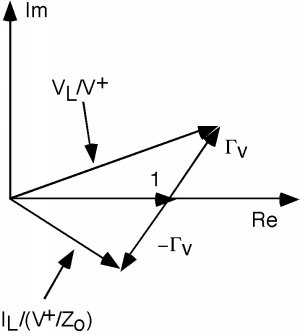
As we move down the line, the two "$\Gamma$" vectors rotate around at a rate of $-2\beta s$as shown in Figure \(\PageIndex{4}\). As they rotate, one vector gets longer and the other gets shorter, and then the opposite occurs. In any event, to get $Z\left(s\right)$ we have to divide the first vector by the second. In general, this is not easy to do, but there are some places where it is not too bad. One of these is when $2\beta s=-{\theta }_{\Gamma }$, which is shown in Figure \(\PageIndex{5}\).

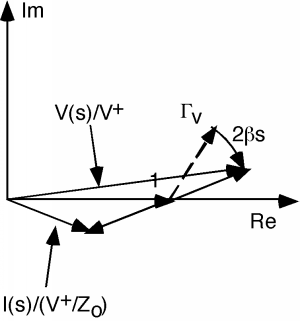
Figura\(\PageIndex{4}\):  Rotación de los fasores en el diagrama de manivela

Figura\(\PageIndex{5}\): Rotating a crank diagram to a $V_{\max }$

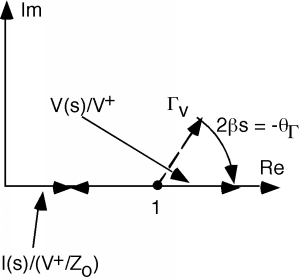
At this point, the voltage vector has rotated around so that it is just lying on the real axis. Obviously its length is now $1+\left|\Gamma \right|$. By the same token, the current vector is also lying on the real axis, and has a length $1-\left|\Gamma \right|$. Dividing one by the other, and multiplying by $Z_0$ gives us $Z\left(s\right)$ at this point.

$$Z\left(s\right)=Z_0\frac{1+\left|{\Gamma }_{\nu }\right|}{1-\left|{\Gamma }_{\nu }\right|}$$

Where is this point, and does it have any special meaning? For this, we need to go back to our expression for $V\left(s\right)$ in this equation.

$$\begin{array}{rcl}\hfill V\left(s\right)& \hfill =\hfill & V^{+}{e}^{i\beta s}(1+{\Gamma }_{\nu }{e}^{-2i\beta s})\hfill \\ \hfill & \hfill =\hfill & V^{+}{e}^{i\beta s}(1+\left|{\Gamma }_{\nu }\right|e^{i({\theta }_{\Gamma }-2\beta s)})\hfill \\ \hfill & \hfill =\hfill & V^{+}{e}^{i\beta s}(1+\left|{\Gamma }_{\nu }\right|e^{i\phi \left(s\right)})\hfill \end{array}$$

where we have substituted $\left|{\Gamma }_{\nu }\right|e^{i\theta }$ for the phasor ${\Gamma }_{\nu }$ and then defined a new angle $\phi \left(s\right)={\theta }_{\Gamma }-2\beta s$.

Now let's find the magnitude of $V\left(s\right)$. To do this we need to square the real and imaginary parts, add them, and then take the square root.

$$\begin{array}{rcl}\hfill \left|V\left(s\right)\right|& \hfill =\hfill & \left|V^{+}\right|(1+\left|{\Gamma }_{\nu }\right|e^{i\phi \left(s\right)})\hfill \\ \hfill & \hfill =\hfill & \left|V^{+}\right|\sqrt{{\left(1+\left|{\Gamma }_{\nu }\right|\cos \left(\phi \left(s\right)\right)\right)}^2+{\left(\left|{\Gamma }_{\nu }\right|\right)}^2{\sin }^2\left(\phi \left(s\right)\right)}\hfill \end{array}$$

so,

$$\left|V\left(s\right)\right|=\left|V^{+}\right|\sqrt{1+2\left|{\Gamma }_{\nu }\right|\cos \left(\phi \left(s\right)\right)+{\left(\left|{\Gamma }_{\nu }\right|\right)}^2{\cos }^2\left(\phi \left(s\right)\right)+{\left(\left|{\Gamma }_{\nu }\right|\right)}^2{\sin }^2\left(\phi \left(s\right)\right)}$$

which, since ${\sin }^2\left(·\right)+{\cos }^2\left(·\right)=1$

$$\left|V\left(s\right)\right|=\left|V^{+}\right|\sqrt{1+{\left(\left|{\Gamma }_{\nu }\right|\right)}^2+2\left|{\Gamma }_{\nu }\right|\cos \left(\phi \left(s\right)\right)}$$

Remember, $\phi \left(s\right)$ is an angle which changes with $s$. In particular, $\phi \left(s\right)={\theta }_{\Gamma }-2\beta s$. Thus, as we move down the line $\left|V\left(s\right)\right|$ will oscillate as $\cos \left(\phi \left(s\right)\right)$ oscillates. A typical plot for $V\left(s\right)$ (for $\left|{\Gamma }_{\nu }\right|=0.5$ and ${\theta }_{\Gamma }={45}^{°}$) is shown below in Figure \(\PageIndex{6}\).

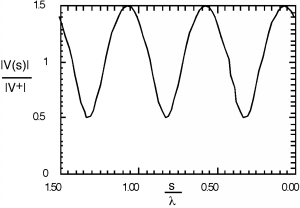
Figura Patrón\(\PageIndex{6}\):  de onda estacionaria