1.5: El Sistema de Amortiguador de Masas II - Resolviendo la ODE LTI de 1er orden para respuesta de tiempo, dada una excitación de pulso y un IC

Una entrada de duración limitada, típicamente llamada pulso, es un tipo muy común de excitación impuesta a los sistemas. Por ejemplo, cuando un martillo golpea un clavo, la fuerza impuesta sobre el clavo por el martillo es un pulso. Un pulso real, como la fuerza de impacto de martillo, a menudo se modela como un pulso de medio seno. Que la fuerza que actúa sobre la masa en la Figura 1.3.1 sea el pulso de medio seno descrito por la siguiente figura y Ecuación\(\ref{eqn:1.5}\):

Figura\(\PageIndex{1}\): Pulso de medio seno.

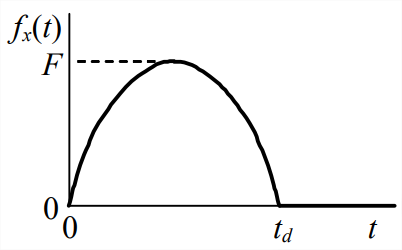
\ [f_ {x} (t) =\ left\ {\ begin {array} {l}
F\ sin\ left (\ pi\ frac {t} {t_ {d}}\ right), 0\ leq t\ leq t_ {d}\\
0, t_ {d} <t
\ end {array}\ right. \ label {eqn:1.5}\]

En Ecuación\(\ref{eqn:1.5}\) para\(f_x(t)\),\(t_d\) denota la duración del pulso. La notación será más manejable en este problema si expresamos la sinusoide variable en el tiempo en la forma\(\sin \omega t\), donde\(\omega\) denota la frecuencia circular de oscilación, en radianes por segundo. En este caso, claramente la frecuencia circular se expresa en términos de la duración del pulso como\(\omega = \pi /t_d\). Especificemos que la velocidad inicial de la masa en el tiempo\(t\) = 0 es algún valor conocido\(v_0\). El enunciado matemático del problema para encontrar la velocidad tiempo-historia es:

\ [\ subrayado {\ texto {ODE}:}\ quad m\ punto {v} +c v=f_ {x} (t)\
\\ subrayado {\ texto {IC}:}\ quad v (0) =v_ {0}\
\ subrayado {\ texto {Buscar}:}\ quad v (t)\ quad\ texto {para todos}\ cuádruple t>0\ nonumber\]

Para resolver este problema en forma cerrada, utilizaremos un método con el que deberías estar familiarizado a partir de tu estudio previo de ODEs. Primero, encontramos la solución homogénea (también llamada complementaria)\(v_h(t)\), que es la solución de la ODE homogénea, la versión de la Ecuación 1.3.3 con el lado derecho cero:

\[m \dot{v}_{h}+c v_{h}=0\label{eqn:1.6} \]

Una ODE LTI homogénea siempre tiene soluciones en potencias lineales de tiempo de\(e\) = 2.71828... (la base de logaritmos naturales), con algunos coeficientes constantes inicialmente desconocidos:

\[v_{h}(t)=C e^{\lambda t}, \nonumber \]

en el que las constantes\(C\) y\(\lambda\) son desconocidas en esta etapa. Para encontrar\(\lambda\), sustituimos la solución en la ODE homogénea\(\ref{eqn:1.6}\):

\[m C \lambda e^{\lambda t}+c C e^{\lambda t}=(m \lambda+c) C e^{\lambda t}=0 \nonumber \]

Si\(Ce^{\lambda t}\) = 0, obtenemos la solución trivial inútil\(v_h(t)\) = 0, por lo que una solución útil requiere que t\(m\lambda + c\) = 0, que se conoce como la ecuación característica de la ODE. La solución de esta ecuación da el llamado valor característico,\(\lambda\) =\(-c/m\), que conduce a:

\[v_{h}(t)=C e^{-(c / m) t}\label{eqn:1.7} \]

Tenga en cuenta que todavía no hemos resuelto por constante\(C\). Podemos encontrar\(C\) solo después de haber determinado una solución particular, también conocida como la solución no homogénea porque es una solución que satisface la ecuación ODE completa 1.3.3 para el lado derecho dado\(f_x(t)\). Para este problema, necesitaremos dos soluciones particulares, porque\(f_x(t)\) se define de manera diferente a lo largo de dos intervalos de tiempo diferentes, Ecuación\(\ref{eqn:1.5}\). Primero, encontramos una solución particular\(v_p(t)\) válida sobre la duración del pulso, 0\(\leq\)\(t\)\(\leq\)\(t_d\), para lo cual la ODE es:

\[m \dot{v}_{p}+c v_{p}=F \sin \omega t, \text { where } \omega=\pi / t_{d}\label{eqn:1.8} \]

Para encontrar un particular\(v_p(t)\) que satisfaga la Ecuación ODE\(\ref{eqn:1.8}\), aplicamos el método de coeficientes indeterminados, lo que implica hacer una suposición educada del carácter funcional de la solución, utilizando coeficientes multiplicativos que se determinarán sustituyendo al candidato solución de nuevo en Ecuación ODE\(\ref{eqn:1.8}\). La función sinusoidal del lado derecho de la ecuación ODE\(\ref{eqn:1.8}\) tiene un conjunto finito de derivadas: la derivada de un seno es un coseno, la derivada de un coseno es un seno, etc. Por lo tanto, asumimos una forma de solución que consiste en una suma lineal de la función y todas sus derivadas:

\[v_{p}(t)=P_{1} \sin \omega t+P_{2} \cos \omega t, \nonumber \]

con coeficientes\(P_1\) e\(P_2\) indeterminados en esta etapa. Sustituya esta solución candidata de nuevo a la ecuación ODE\(\ref{eqn:1.8}\):

\[m \omega\left(P_{1} \cos \omega t-P_{2} \sin \omega t\right)+c\left(P_{1} \sin \omega t+P_{2} \cos \omega t\right)=F \sin \omega t \nonumber \]

Recoge términos que se multiplican\(\sin\omega t\) y\(\cos\omega t\) en ambos lados de la ecuación:

\[\left(-m \omega P_{2}+c P_{1}\right) \sin \omega t+\left(m \omega P_{1}+c P_{2}\right) \cos \omega t=(F) \sin \omega t+(0) \cos \omega t \nonumber \]

Las funciones\(\sin\omega t\) y\(\cos\omega t\) son linealmente independientes entre sí, lo que requiere que los términos del lado izquierdo y del lado derecho que se multiplican\(\sin\omega t\) deben igualarse entre sí, y lo mismo para los términos que multiplican cosωt, lo que lleva a dos ecuaciones algebraicas para los coeficientes \(P_1\)y\(P_2\):

\[c P_{1}-m \omega P_{2}=F \quad \text { and } \quad m \omega P_{1}+c P_{2}=0 \nonumber \]

La segunda ecuación da\(P_2=-(m\omega/c)P_1\), y sustituirla en la primera ecuación para eliminar\(P_2\) conduce a:

\[P_{1}=\frac{c F}{(m \omega)^{2}+c^{2}} \quad \text { and } \quad P_{2}=\frac{-m \omega}{c} P_{1}\label{eqn:1.9} \]

En lugar de escribir fórmulas algebraicas desordenadas para todos los coeficientes en este problema, es conveniente expresar todos los demás en términos de\(P_1\) y\(P_2\), como es en Ecuación\(\ref{eqn:1.9}\).

Para obtener la solución completa para la duración del pulso, 0\(\leq\)\(t\)\(\leq\)\(t_d\), ahora combinamos las soluciones homogéneas y particulares:

\[v(t)=v_{h}(t)+v_{p}(t)=C e^{-(c / m) t}+P_{1} \sin \omega t+P_{2} \cos \omega t, \text { for } 0 \leq t \leq t_{d}\label{eqn:1.10} \]

Aún no\(\ref{eqn:1.10}\) se conoce el coeficiente\(C\) en la ecuación; pero ahora, finalmente, podemos aplicar la condición inicial (IC) para determinar\(C\):

\[v(0)=v_{0}=C(1)+P_{1}(0)+P_{2}(1) \Rightarrow C=v_{0}-P_{2}=v_{0}+(m \omega / c) P_{1}\label{eqn:1.11} \]

Ecuaciones\(\ref{eqn:1.9}\) a través de\(\ref{eqn:1.11}\) describir la respuesta de velocidad durante la duración del pulso\(\leq\)\(t\)\(\leq\)\(t_d\), 0, por lo que todavía necesitamos encontrar la respuesta post-pulso, para\(t_d\) <\(t\). Para ello, debemos reconocer dos hechos: (1)\(f_x(t)\) = 0 for\(t_d\) <\(t\); y (2) la velocidad\(v(t)\) no puede cambiar repentinamente at\(t\) =\(t_d\) (porque la aceleración no puede ser infinita), más bien, la velocidad debe ser igual Ecuación\(\ref{eqn:1.10}\) evaluada en\(t\) =\(t_d\) . El hecho 1 significa que la ODE for\(t_d\) <\(t\) es homogénea; de ahí que la solución particular sea cero, y solo tenemos una solución homogénea, pero ahora con un coeficiente diferente,\(D\), que antes:

\[v(t)=D e^{-(c / m) t}, \text { for } t_{d}<t\label{eqn:1.12} \]

Para encontrar\(D\), usamos el Hecho 2, que esencialmente es el IC para\(t_d\) <\(t\), y la Ecuación\(\ref{eqn:1.10}\):

\[D e^{-(c / m) t_{d}}=v\left(t_{d}\right)=C e^{-(c / m) t_{d}}+P_{1} \sin \omega t_{d}+P_{2} \cos \omega t_{d}\label{eqn:1.13} \]

\[\Rightarrow \quad D=v\left(t_{d}\right) e^{(c / m) t_{d}} \nonumber \]

\[\Rightarrow \quad v(t)=v\left(t_{d}\right) e^{-\frac{c}{m}\left(t-t_{d}\right)}, \text { for } t_{d}<t \label{eqn:1.14} \]

Ecuación\(\ref{eqn:1.14}\), con Ecuación\(\ref{eqn:1.13}\) para\(v(t_d)\), combinada con Ecuación\(\ref{eqn:1.9}\) y Ecuación\(\ref{eqn:1.11}\) para coeficientes\(P_1\)\(C\),\(P_2\) y, representa la respuesta para\(t_d\) <\(t\). Debido a que la masa\(m\) y la constante de amortiguación viscosa\(c\) son cantidades físicas positivas, la ecuación\(\ref{eqn:1.14}\) es una decadencia exponencial pura, que se acerca a cero como\(t \rightarrow \inf\).