1.10: El Sistema Masa-Muelle - Resolviendo una ODE LTI de 2do orden para Respuesta de Tiempo
- Page ID
- 84630
Supongamos que tenemos un sistema del tipo representado en la Figura 1.9.1 para el cual la fuerza de amortiguación\(c\dot{x}\), en la Ecuación 1.9.6, es insignificantemente pequeña en comparación con la fuerza inercial\(m\ddot{x}\) y la fuerza estructural\(kx\). La figura\(\PageIndex{1}\) es una fotografía de un sistema real 1 con tan poca amortiguación que, en algunas circunstancias, podemos descuidar la fuerza de amortiguación. El carro de masa de este sistema se desplaza hacia adelante y hacia atrás sobre rodamientos lineales de baja fricción, los cuales están encerrados debajo del carro y no son visibles en la fotografía. La longitud total de este sistema, desde el extremo izquierdo (fijo) del muelle, hasta el borde más derecho del carro de masa es de 8\(\frac{1}{2}\) pulgadas (21.6 cm), y cada una de las tres losas metálicas de color claro unidas al carro tiene masa de\(\frac{1}{2}\) kilogramo.

Si podemos descuidar la fuerza de amortiguación en un sistema como el de la Figura\(\PageIndex{1}\), entonces el término\(c\dot{x}\) cae fuera de la Ecuación 1.9.6, y nos quedamos con la ODE de segundo orden más simple,
\[m \ddot{x}+k x=f_{x}(t)\label{eqn:1.18} \]
Si conocemos los CI (Ecuación 1.9.5) y la fuerza de excitación\(f_x(t)\), entonces podemos resolver la Ecuación\(\ref{eqn:1.18}\) para\(x(t)\). Para referencia futura, tenga en cuenta que la cantidad de masa\(m\) y la constante de rigidez del resorte\(k\) son valores intrínsecamente positivos. También, observe que se\(f_x(t)\) puede aplicar al sistema de la Figura\(\PageIndex{1}\) a través del eslabón visible en el lado derecho del carro de masa.
Será instructivo determinar una respuesta temporal para este sistema masa-resorte (\(m-k\)) de segundo orden, aplicando el procedimiento estándar de solución ODE descrito en la Sección 1.5. Encontraremos la solución algebraica completa como la suma de soluciones homogéneas y particulares,\(x(t) = x_h(t)+x_p(t)\). Supongamos que en el tiempo\(t\) = 0 el resorte no está deformado y la masa está en reposo, de modo que ICs Ecuación 1.9.5 son
\[\dot{x}(0)=0 \text { and } x(0)=0\label{eqn:1.19} \]
Supongamos también que la excitación es un pulso de fuerza descrito por la ecuación\(f_x(t) = F_m(t/t_m)e^{(1-t/t_m)}\); al aplicar cálculo a esta función, puede demostrar fácilmente que sube de cero a\(t\) = 0 al valor máximo\(F_m\) en el tiempo\(t\) =\(t_m\), y, a partir de entonces, vuelve a caer gradualmente a cero (ver Figura\(\PageIndex{2}\)). En dinámica, una función lineal del tiempo como\(t/t_m\) suele denominarse función de “rampa”; dado que nuestra excitación consiste en una función exponencial decreciente multiplicada por una función de rampa, llamamos a esta excitación un pulso de fuerza “exponencial en rampa”.
La ODE homogénea asociada a la Ecuación\(\ref{eqn:1.18}\) es\(m\ddot{x}_h+kx_h=0\). Echamos esta ecuación en una forma familiar dividiendo por masa\(m\) y definiendo la cantidad positiva\(\omega^2_n=k/m\), dando a la ODE
\[\ddot{x}_{h}+\omega_{n}^{2} x_{h}=0\label{eqn:1.20} \]
La raíz positiva\(\omega_n = \sqrt{k/m}\) se llama la frecuencia natural de este\(m-k\) sistema, y\(\omega_n\) tiene significación física que se discutirá a continuación con la solución final. Tal vez recuerde de su estudio anterior de ODEs, o puede verificar fácilmente mediante la sustitución en Ecuación\(\ref{eqn:1.20}\), que la solución se puede expresar como
\[x_{h}(t)=C_{1} \sin \omega_{n} t+C_{2} \cos \omega_{n} t\label{eqn:1.21} \]
Constantes\(C_1\) y\(C_2\) son desconocidas en este punto del proceso de solución.
Con excitación por el pulso exponencial inclinado definido anteriormente, cualquier solución en particular\(x_p(t)\) debe satisfacer la ODE no homogénea
\[m \ddot{x}_{p}+k x_{p}=F_{m}\left(t / t_{m}\right) e^{\left(1-t / t_{m}\right)}\label{eqn:1.22} \]
Para encontrar un particular\(x_p(t)\) que satisfaga la Ecuación ODE\(\ref{eqn:1.22}\), aplicamos el método de coeficientes indeterminados, al igual que en la Sección 1.5. Es fácil demostrar por sucesivas diferenciaciones que todas las derivadas con respecto al tiempo de la función\((t/t_m)e^{(1-t/t_m)}\) producen solamente múltiplos constantes de\((t/t_m)e^{(1-t/t_m)}\) sí misma, y de\(e^{(1-t/t_m)}\). Por lo tanto, buscamos una solución particular que consista en una suma lineal de estas dos funciones:
Determinamos las constantes\(P_1\) y\(P_2\) sustituyendo Ecuación\(\ref{eqn:1.23}\) en Ecuación\(\ref{eqn:1.22}\), igualando los coeficientes de\((t/t_m)e^{(1-t/t_m)}\) y\(e^{(1-t/t_m)}\) en los dos lados de la ecuación algebraica resultante, y luego resolviendo para\(P_1\) y\(P_2\) [tarea Problema 1.10 (a)]. Este proceso produce los resultados
La solución completa (pero aún no definitiva) es
Ahora podemos determinar las constantes desconocidas restantes sustituyendo Ecuación\(\ref{eqn:1.25}\) en Ecuación ICs\(\ref{eqn:1.19}\),\(\dot{x}(0)\) = 0 y\(x(0)\) = 0, y resolviendo algebraicamente para constantes\(C_1\) y\(C_2\) [tarea Problema 1.10 (b)]. Los resultados son
La solución completa y final es Ecuación\(\ref{eqn:1.25}\), con constantes\(C_1\),\(C_2\),\(P_1\), y\(P_2\) definidas en términos de los parámetros básicos\(m\),,\(k\)\(F_m\), y\(t_m\) por Ecuaciones\(\ref{eqn:1.24}\) y\(\ref{eqn:1.26}\). Vamos a calcular y trazar una respuesta de tiempo para el sistema de Figura\(\PageIndex{1}\). La masa total del carro más las losas metálicas unidas de tres\(\frac{1}{2}\) kilogramos es\(m\) = 2.20 kg, y la rigidez del resorte es\(k\) = 770 N/m. Supongamos que el impulso de fuerza exponencial en rampa tiene un valor máximo\(F_m\) = 6 N en el instante\(t_m\) = 1/12 s. El MATLAB líneas de comando en la página siguiente calculan e imprimen la cantidad de frecuencia\(f_n\) =\(\omega_n/2\pi\), y calculan y trazan la respuesta de tiempo en el intervalo 0\(\leq\)\(t\)\(\leq\) 2 s. Tenga en cuenta que no fue necesario ensamblar estas líneas de comando en un archivo M formal; más bien, el las líneas se compusieron en un programa de edición de texto, luego se copió todo el grupo de líneas y se pegó en el prompt “>>” en la ventana de comandos de MATLAB. Además, dado que la solución Ecuación\(\ref{eqn:1.25}\) incluye el producto de dos funciones de tiempo en el término\((t/t_m)e^{(1-t/t_m)}\), es necesario implementar este producto utilizando la multiplicación de matrices MATLAB (. *) en la operación prod=tt. *efun.
>> %respuesta masa-resorte: CI en reposo; entrada de pulso exponencial en rampa m=2.20; k=770;% masa y rigidez del sistema, unidades SI wn=sqrt (k/m); fn=wn/2/pi; disp ('Frecuencia natural (ciclos/seg) fn ='), disp (fn) Fm=6.0; tm=1/12; %parámetros de excitación t=0:. 005:2; %secuencia de tiempo para excitación/respuesta tt=t/tm; efun=exp (1-tt); prod=tt. *efun; f=FM*prod; %excitación a1=m/tm^2; a2=a1+k; p1=FM/a2; P2=2*a1*p1/a2; %P constantes C1= (P2-P1) *exp (1) /wn/tm; C2=-p2*exp (1); %C constantes wt=wn*t; x=C1*sin (wt) +C2*cos (wt) +P1*PROD+P2*EFUN; %gráfica de respuesta (t,100*f/k, 'k.' , t,100*x, 'k'), grid, xlabel ('Tiempo t [seg] '),... ylabel ('Traducciones referencia f_x (t) /k y x real (t) [cm]'),... title ('Respuesta del sistema masa-resorte al impulso exponencial en rampa')
Frecuencia natural (ciclos/seg) fn = 2.9775
La figura\(\PageIndex{2}\) es el gráfico de MATLAB producido por la secuencia de comandos anterior. La gráfica se editó en la ventana de figura de MATLAB, principalmente para reducir el tamaño y agregar la leyenda.
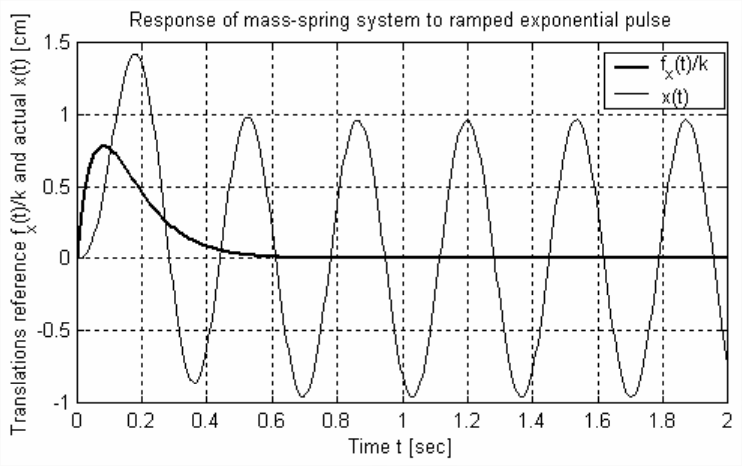
La cantidad de referencia\(f_x(t)/k\) trazada en la Figura\(\PageIndex{2}\) representa la fuerza de excitación, pero dividida por\(k\), de manera que tiene las unidades de traslación. Se puede ver en la Ecuación ODE básica\(\ref{eqn:1.18}\)\(m \ddot{x}+k x=f_{x}(t)\),, que la cantidad trazada representa físicamente la deformación elástica que\(f_{x}(t)\) produciría la excitación dinámica si la masa\(m\) fuera cero o insignificante. Debido a que esta cantidad de referencia se calcula por descuido de toda la fuerza inercial dinámica\(m\ddot{x}\), a menudo se le llama la respuesta pseudo-estática.
Observe en la Figura\(\PageIndex{2}\) que la traslación dinámica real\(x(t)\) de la masa sobrepasa en gran medida la traslación pseudo-estática inicialmente (con una respuesta máxima de aproximadamente +1.4 cm a aproximadamente 0.18 s), y que la respuesta real persiste como vibración significativa después de que la excitación del pulso haya se extinguieron. Estas son características dinámicas importantes de muchos sistemas que encontramos en la práctica de ingeniería. En realidad, todos los sistemas mecánicos que consisten en masas puramente pasivas y miembros estructurales pasivos tienen cierto grado de amortiguación positiva; pero, si las fuerzas de amortiguación son bajas en comparación con las fuerzas inerciales y estructurales, entonces estos sistemas reales responderán a la excitación de manera similar, al menos en un sentido cualitativo, a la respuesta “real” de la Figura\(\PageIndex{2}\). Por ejemplo, el sistema real de la Figura\(\PageIndex{1}\) está amortiguado positiva pero ligeramente; en respuesta al pulso de fuerza dado, este sistema experimentaría casi la misma respuesta inicial y sobreimpulso como se muestra en la Figura\(\PageIndex{2}\), pero la vibración moriría gradualmente, y el movimiento cesaría por completo después de tres o cuatro segundos.
Los términos en Ecuación\(\ref{eqn:1.25}\) que representan principalmente vibración son las funciones sinusoidales\(\sin\omega_n t\) y\(\cos\omega_n t\), siendo el argumento ángulo (en radianes) de estas funciones periódicas\(\theta(t)\) =\(\omega_n t\). El periodo de dicha función es el tiempo requerido para que la función complete un ciclo completo y comience a repetirse. En este caso, denotemos ese periodo como\(T_n\) y observemos que sus unidades físicas naturales son segundos/ciclo. La frecuencia asociada\(f_n\), en las unidades ciclos/segundo, 2 es obviamente solo la inversa del periodo,\(f_n=1/T_n\). Así, el argumento ángulo (en radianes) de las funciones sinusoidales periódicas se puede escribir en las siguientes formas equivalentes:\(\theta (t)\) =\(\omega_n t\) =\(2\pi (t/T_n\) =\(2\pi f_n t\). La relación importante entre la frecuencia natural circular\(\omega_n\), en radianes/segundo, y la frecuencia natural cíclica\(f_n\), en ciclos/segundo, es\(f_n\) =\(\omega_n/2\pi\). Para los valores de masa\(m\) y rigidez\(k\) utilizados en los cálculos de MATLAB anteriores, el valor de impresión de\(f_n\) es de 2.98 ciclos por segundo, y esta es la frecuencia que es más obvia en la Figura\(\PageIndex{2}\); por ejemplo, tan cerca como podemos detectar a ojo, casi exactamente tres ciclos completos de vibración ocurren entre\(t\) = 0.7 s y\(t\) = 1.7 s.
1 Esto es parte de una Planta Rectilineal Modelo 210a diseñada y fabricada por Educational Control Products de Bell Canyon, California, USA.
2 Más comúnmente en la terminología moderna, un ciclo/segundo se designa como un hercio, con la abreviatura Hz.


