3.5: Rodamiento Inducido por Ailerón de un Avión o Misil

La principal fuente de la teoría aerodinámica de esta sección es Nelson, 1989, páginas 19-20, 153-156 y 250-260. El momento de balanceo aerodinámico en un avión o misil está escrito en notación aeronáutica estándar como

\[\begin{align} L(t) &=\frac{\partial L}{\partial \delta} \delta(t)+\frac{\partial L}{\partial p} p(t) \\[4pt] &\equiv L_{\delta} \delta(t)+L_{p} p(t) \label{eqn:3.11} \end{align} \]

Existe una ambigüedad notacional entre el momento\(L(t)\) y el operador de transformación de Laplace\(L[f(t)]\) introducido en el Capítulo 2; tales ambigüedades son inevitables en el trabajo técnico, por lo que debes acostumbrarte a ellas.

El ángulo de balanceo (inclinación) (en radianes) es\(\theta(t)\), definido aquí como positivo en el sentido de las agujas del reloj como lo ve un observador detrás del vehículo, es decir, balanceo hacia la derecha (Figura\(\PageIndex{1}\)). En la Ecuación\(\ref{eqn:3.11}\),\(\delta(t)\) se encuentra el ángulo de desviación del alerón de entrada (en radianes) para producir balanceo, el alerón derecho se desvía hacia arriba y el alerón izquierdo desviado hacia abajo para producir una tasa de balanceo positiva,\(p(t) \equiv \dot{\theta}\) (rad/s).

Figura\(\PageIndex{1}\): Rodamiento inducido por alerón de un avión

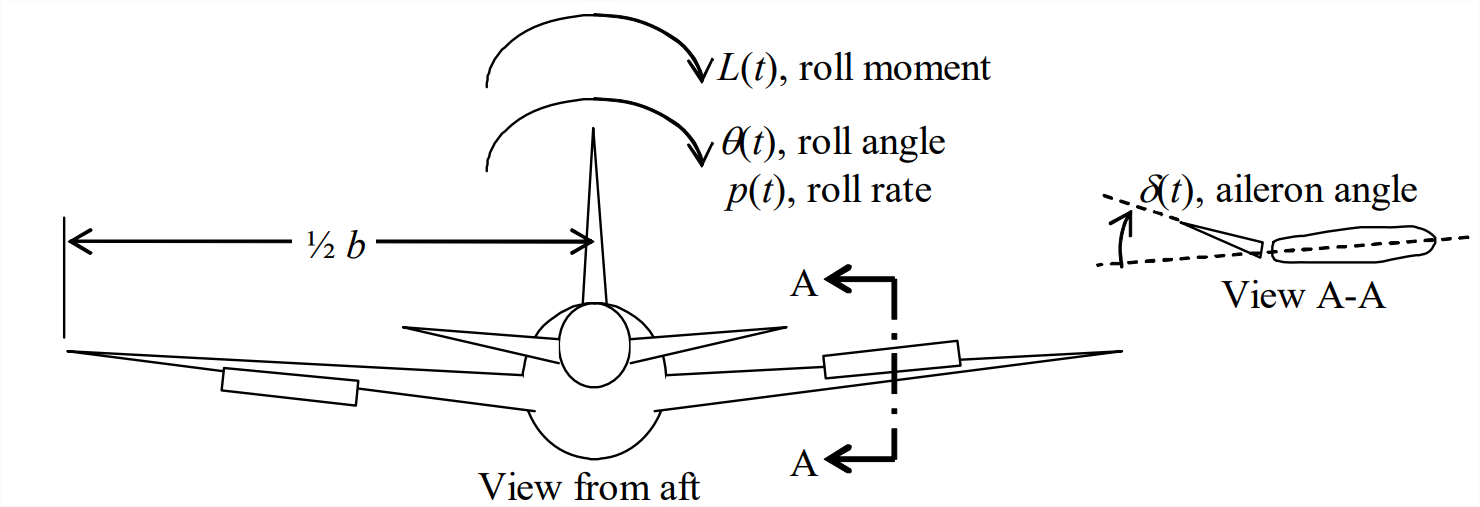
Las derivadas aerodinámicas dimensionales en la Ecuación\(\ref{eqn:3.11}\) se relacionan con coeficientes adimensionales por:

\[L_{\delta}=\bar{q} S b C_{\delta}>0 \quad\left(\frac{1 b-f t}{r a d} \text { or } \frac{N-m}{r a d}\right)\label{eqn:3.12} \]

\[L_{p}=\bar{q} S b \frac{b}{2 V} C_{p}=\frac{\bar{q} S b^{2}}{2 V} C_{p}<0 \quad\left(\frac{1 \mathrm{b}-\mathrm{ft}}{\mathrm{rad} / \mathrm{sec}} \operatorname{or} \frac{\mathrm{N}-\mathrm{m}}{\mathrm{rad} / \mathrm{sec}}\right)\label{eqn:3.13} \]

Las constantes en Ecuaciones\(\ref{eqn:3.12}\) y\(\ref{eqn:3.13}\) se definen como:

• \(\bar{q}=\frac{1}{2} \rho V^{2}\)es la presión dinámica de flujo libre (lb/ft ² o N/m ²)
• \(\rho\)es la densidad del aire (slug/ft ³ o kg/m ³)
• \(V\)es la velocidad del aire de flujo libre (pies/s o m/s)
• \(S\)es el área de forma plana del ala (ft ² o m ²)
• \(b\)es la envergadura completa del ala (ft o m)
• \(C_{\delta}>0\)es el coeficiente de momento de estabilidad aerodinámica adimensional (rad ⁻¹), momento de rodadura debido a la deflexión del alerón (una función del número de Mach)
• \(C_p <0\)es el coeficiente de momento de estabilidad aerodinámica adimensional (rad ⁻¹), amortiguación del balanceo debido a la velocidad de balanceo (una función del número de Mach).

El término\(b / 2 V\) en Ecuación\(\ref{eqn:3.13}\), el momento de amortiguación debido a la tasa de balanceo, amerita alguna explicación. La velocidad de balanceo en el sentido de las agujas del reloj de la punta del ala derecha es\(p \times b / 2\), por lo que el ángulo de ataque adicional inducido en la punta del ala por la velocidad de balanceo es\(\tan ^{-1}\left[\frac{p b / 2}{V}\right] \approx \frac{p b}{2 V}\), un ángulo pequeño (la magnitud del ángulo es exagerada en la Figura\(\PageIndex{2}\), solo para mejorar la claridad). Así,\(\frac{b}{2 V} p(t)\) en Eqsuations\(\ref{eqn:3.13}\) y\(\ref{eqn:3.11}\) juega el mismo papel que el de\(\delta(t)\) en Eqs. \(\ref{eqn:3.12}\)y\(\ref{eqn:3.11}\).

La segunda ecuación de ^la ley de Newton de movimiento para rodar es\(J \ddot{\theta} \equiv J \dot{p}=L(t)\), en la que\(J\) (slug-ft2 o kg-m2) es la inercia rotacional del vehículo alrededor de su eje de rodadura. Esta ecuación se basa en la suposición de que el vehículo solo puede rodar (es decir, sin acoplamiento con otros grados de libertad como el desplazamiento lateral y la guiñada). Sustitución de Eqs. \(\ref{eqn:3.11}\)-\(\ref{eqn:3.13}\) en la ley de Newton da:

\[J \dot{p}=L_{\delta} \delta+L_{p} p \Rightarrow J \dot{p}-L_{p} p=L_{\delta} \delta \nonumber \]

\[\Rightarrow \quad \dot{p}+\left(\frac{-L_{p}}{J}\right) p=\left(\frac{-L_{p}}{J}\right)\left(\frac{L_{\delta}}{-L_{p}}\right) \delta(t)=\left(\frac{-L_{p}}{J}\right) \frac{2 V}{b}\left(\frac{C_{\delta}}{-C_{p}}\right) \delta(t)\label{eqn:3.14} \]

Escribir Ecuación\(\ref{eqn:3.14}\) en forma ^estándar de primer orden La ecuación 3.4.8 da [con\(b\) en la Ecuación 3.4.8 temporalmente reemplazada por\(B\) para reducir la ambigüedad notacional]:

\[\dot{p}+\frac{1}{\tau_{1}} p=B \delta(t)\label{eqn:3.15} \]

en la que tenemos, respectivamente, constante de tiempo\(\tau_1\) y constante\(B\):

\[\tau_{1}=\frac{J}{-L_{p}}=\frac{2 V J}{\bar{q} S b^{2}\left(-C_{p}\right)}=\frac{4 J}{\rho V S b^{2}\left(-C_{p}\right)}>0\label{eqn:3.16} \]

\[B=\left(\frac{-L_{p}}{J}\right) \frac{2 V}{b}\left(\frac{C_{\delta}}{-C_{p}}\right)=\frac{1}{\tau_{1}} \frac{2 V}{b}\left(\frac{C_{\delta}}{-C_{p}}\right)=\frac{\bar{q} S b C_{\delta}}{J}>0\label{eqn:3.17} \]

Ejemplo\(\PageIndex{1}\)

^{Utilice los resultados de esta sección y la ecuación 3.4.9 de respuesta general de paso de primer orden para calcular la respuesta rodante a una entrada de alerón\(\delta(t)=2.5^{\circ} \mathrm{H}(t)\) escalonado para un hipotético avión de transporte civil de tamaño mediano.} Los siguientes son datos representativos: la inercia rotacional alrededor del eje de rodadura es\(J\) = 4.0e5 slug-ft ², el área en forma de planta del ala es\(S\) = 1 100 ft ², y la envergadura del ala es\(b\) = 90 pies; para vuelo a 10 000 pies de altitud y velocidad del aire de corriente libre\(V\) = 350 ft/s, Los coeficientes de momento de balanceo adimensionales aerodinámicos son\(C_\delta\) = 0.061 por radián y\(C_p\) = -0.34 por radián. A 10 000 pies de altitud, la densidad estándar del aire es\(\rho\) = 0.001 755 slug/ft ³ (Nelson, 1989, p. 248).

Solución

\[\bar{q}=\frac{1}{2} \rho V^{2}=\frac{1}{2} \times 1.755 e-3 \frac{\mathrm{slug}}{\mathrm{ft}^{3}} \times\left(350 \frac{\mathrm{ft}}{\mathrm{s}}\right)^{2}=107.5 \frac{\mathrm{lb}}{\mathrm{ft}^{2}} \nonumber \]

\[L_{p}=\frac{\bar{q} S b^{2}}{2 V} C_{p}=\frac{107.5 \mathrm{lb} / \mathrm{ft}^{2} \times 1,100 \mathrm{ft}^{2} \times(90 \mathrm{ft})^{2}}{2 \times 350 \mathrm{ft} / \mathrm{s}} \times\left(-0.34 \mathrm{rad}^{-1}\right)=-4.65 \mathrm{e} 5 \frac{\mathrm{lb}-\mathrm{ft}}{\mathrm{rad} / \mathrm{s}} \nonumber \]

\[\tau_{1}=\frac{J}{-L_{p}}=\frac{4.0 \mathrm{e} 5 \mathrm{lb}-\mathrm{s}^{2}-\mathrm{ft}}{4.65 \mathrm{e} 5 \mathrm{lb}-\mathrm{s}-\mathrm{ft} / \mathrm{rad}}=0.86 \mathrm{s} \nonumber \]

(Comentarios respecto a las unidades: El ángulo es una cantidad adimensional, por lo que el radián, que es la métrica fundamental del ángulo, no tiene unidades. En el cálculo anterior para\(L_p\), todas las unidades mostradas, incluyendo el radián, se equilibran en el resultado final para dar la unidad resultante correcta,\(\frac{1 \mathrm{b}-\mathrm{ft}}{\mathrm{rad} / \mathrm{s}}\); es importante reconocer esta unidad en contraposición, por ejemplo\(\frac{1 b-f t}{\operatorname{deg} /s}\), a, que sería el caso si\(C_p\) se dieran por grado. Sin embargo, en los cálculos que producen resultados que no son cantidades angulares, como los\(\tau_1\) anteriores, el radián debe reconocerse como sin unidades, y no debe aparecer en las unidades del resultado numérico final. Esta es una característica general que puede confundirnos cuando comprobamos para cerciorarnos de que las unidades de respuestas numéricas son correctas).

\[B=\frac{1}{\tau_{1}} \frac{2 V}{b}\left(\frac{C_{\delta}}{-C_{p}}\right)=\frac{1}{0.86 \mathrm{s}} \times \frac{2 \times 350 \mathrm{ft} / \mathrm{s}}{90 \mathrm{ft}} \times \frac{0.061 \mathrm{rad}^{-1}}{0.34 \mathrm{rad}^{-1}}=1.62 \mathrm{s}^{-2} \nonumber \]

A partir de la Ecuación 3.4.9, la respuesta de velocidad de balanceo a la entrada de paso de 2.5° es

\[p(t)=B U \tau_{1}\left[1-\exp \left(-t / \tau_{1}\right)\right]=1.62 s^{-2} \times 2.5 \operatorname{deg} \times 0.86 s \times\left(1-e^{-t /(0.86 \mathrm{s})}\right) \nonumber \]

\[p(t)=3.5[1-\exp (-1.16 t)] \frac{\text { degrees }}{s} \nonumber \]

La constante de tiempo es\(\tau_{1}\) = 0.86 s, y la velocidad de balanceo en estado estacionario de 3.5 grados/s se logra esencialmente en el tiempo de sedimentación de\(4\tau_{1}\) = 3.44 s.