4.8: Capítulo 4 Tareas

1. ^{Este problema involucra los datos y resultados del sistema amortiguador-resorte de primer orden que se analiza en la Sección 4.2 con el uso del programa MATLAB MatlabDemo41.}
   1. Sustituir los datos de amortiguador-resorte y los valores dados de\(F\) y\(\omega\) en las Ecuaciones 4.3.8 y 4.3.10 para calcular la magnitud\(X\) y el ángulo de fase φ (en grados, en el rango −180°\(\leq\)\(\phi\) < +180°) de la respuesta de frecuencia.
   2. Examine el gráfico de historial de tiempo generado por el programa MATLAB MatlabDemo41. El propósito de este problema es que evalúes esa gráfica como si fuera registrada a partir de un experimento. Consideremos, en particular, el tiempo después de aproximadamente\(t\) = 1.3 s, cuando la salida se ha asentado en respuesta sinusoidal en estado estacionario. Mida de la gráfica la magnitud de salida en estado estacionario\(X\). Mida cualquier información que se requiera de la gráfica, luego calcule el ángulo de fase\(\phi\) (en grados, en el rango −180°\(\leq\)\(\phi\) < +180°) de la respuesta de estado estacionario. Estos resultados experimentales simulados para\(X\) y\(\phi\) deben ser iguales (o al menos cercanos a, ya que no es posible realizar mediciones precisas a partir de una gráfica) los resultados comparables calculados en la parte 1.1 a partir de fórmulas teóricas.
2. ^{Se realiza una prueba experimental de respuesta de frecuencia en un sistema LTI (no necesariamente un sistema de primer orden), con entrada\(u(t)=U \cos \omega t\) y salida\(x(t)=X \cos (\omega t+\phi)\).} A continuación o en la página siguiente se muestra un gráfico simulado [2.1 o 2.2 o 2.3, lo que se asigne] de las cantidades de entrada y salida en estado estacionario a una frecuencia particular. Calcular a partir de la gráfica, con tanta precisión como permitan los datos, los siguientes valores: (i) el periodo sinusoidal\(T_p\), y luego la frecuencia (tanto en Hz como en rad/s), (ii) la relación de magnitud FRF\(X / U\) (asumir unidades físicas consistentes), y (iii) la fase FRF\(\phi\) (en grados, en rango −180°\(\leq\)\(\phi\) < +180°).

   1. 

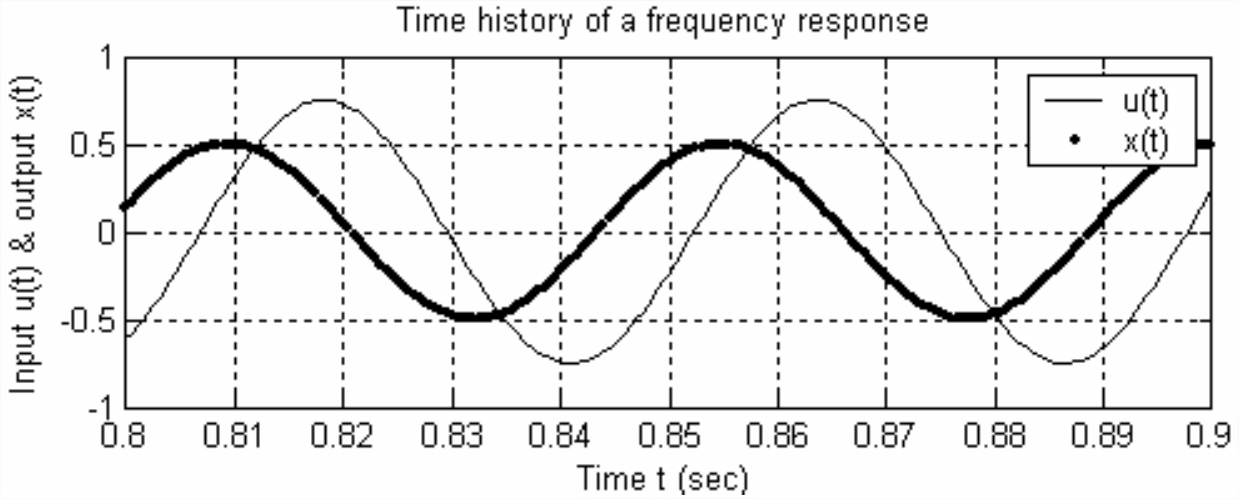
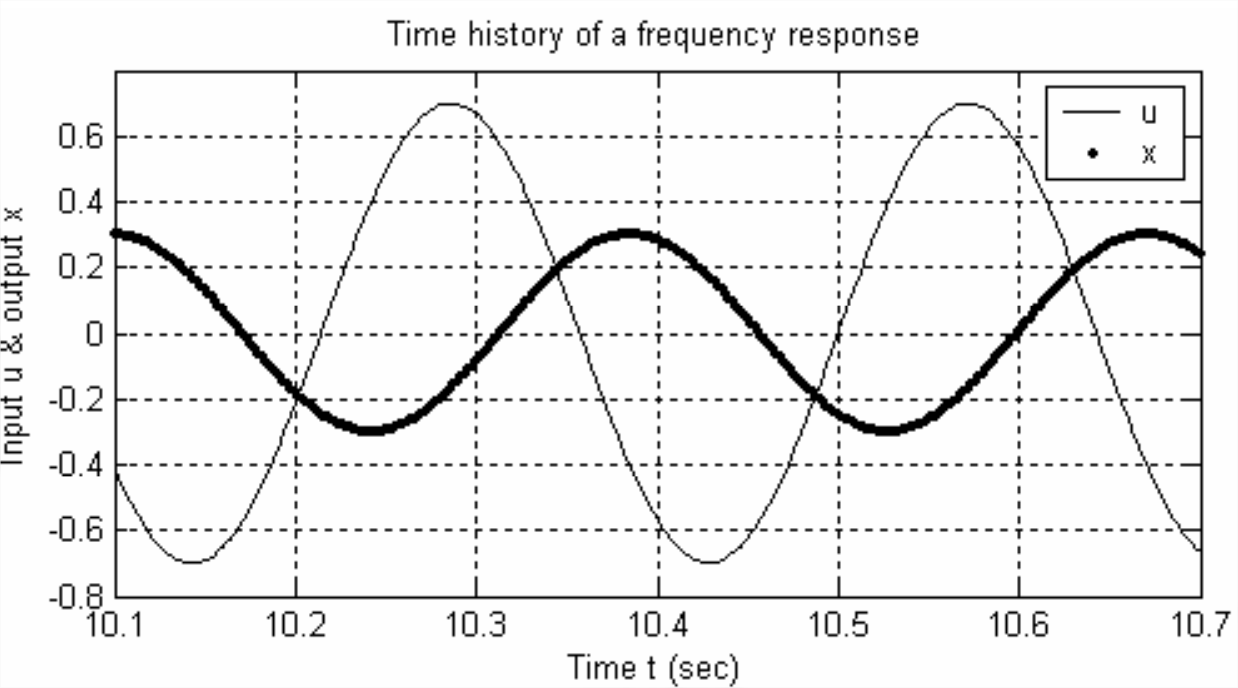
      Figura\(\PageIndex{1}\)

   2. 

      Figura\(\PageIndex{2}\)

   3. 

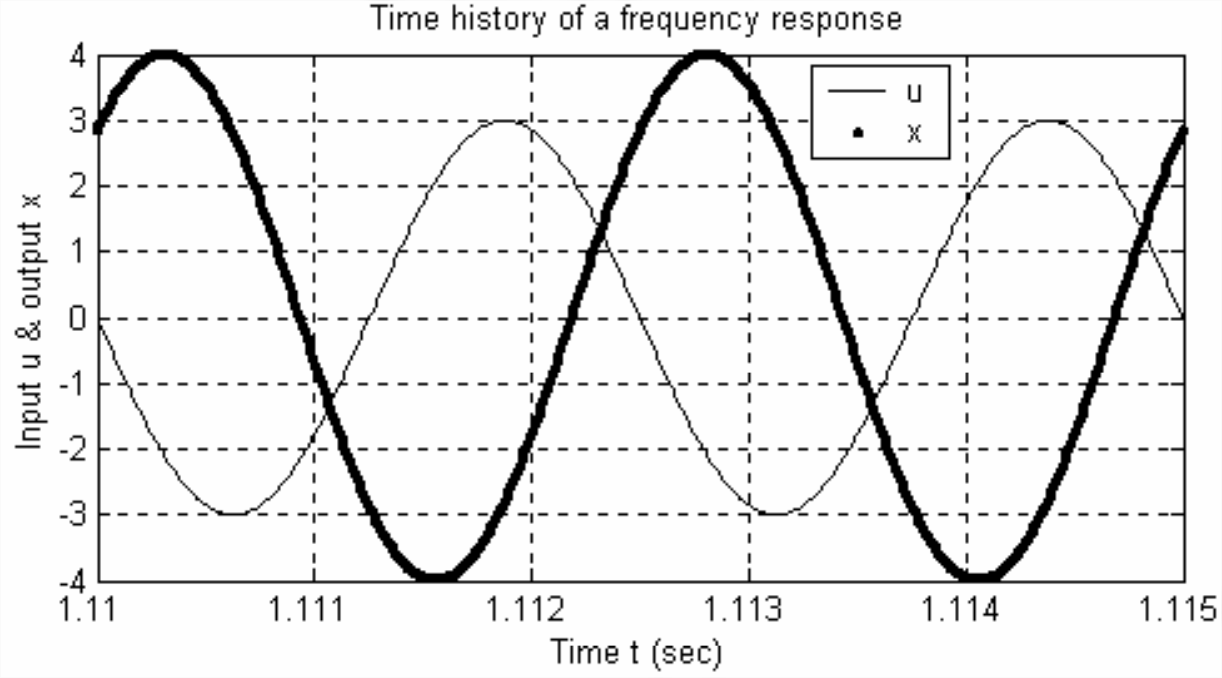
      Figura\(\PageIndex{3}\)

3. La ODE gobernante del filtro paso bajo amortiguador-resorte serie en la Figura 3.7.4 es la Ecuación 3.7.5,\(\tau_{1} \dot{x}_{o}+x_{o}=x_{i}(t)\). ^{Mostrar que la función de frecuencia-respuesta compleja de primer orden asociada es\(F R F(\omega)=T F(j \omega)=1 /\left(1+j \omega \tau_{1}\right)\).} Los siguientes gráficos de script de MATLAB de esta ecuación la relación de magnitud FRF y la fase en un formato convencional (log-log para relación de magnitud, semilog para fase en grados, gráfico de relación de magnitud directamente sobre gráfico de fase), para el caso de constante de tiempo\(\tau_{1}\) = 0.0145 s, con frecuencias de excitación que van de 1 Hz a 1 000 Hz. Tenga en cuenta que MATLAB realiza la mayor parte del trabajo por usted si comienza con el FRF complejo y luego usa la capacidad de MATLAB para realizar aritmética compleja. En particular, la función MATLAB abs calcula el valor absoluto (magnitud) de un número complejo, y el ángulo de la función MATLAB calcula el ángulo en radianes de un número complejo.

   t1=0.0145;% Constante de tiempo del sistema de primer orden (seg)

   f=logspace (0,3,200); w=2*pi*f;% 200 pts. 1 Hz-1 kHz espaciados uniformemente en escala logarítmica

   FRF=1./ (1+j*w*t1);% FRF complejo; tenga en cuenta la necesidad de operación de matriz. /

   magrat=abs (FRF); fazdeg=ángulo (FRF) *180/pi;% relación de magnitud y fase en grados

   subparcela (2,1,1), loglog (f, magrat, 'k'), grid, ylabel ('relación de magnitudes FRF'),...

   title ('FRF del sistema de primer orden con constante de tiempo = 0.0145 seg')

   subparcela (2,1,2), semilogx (f, fazdeg, 'k'), rejilla,...

   ylabel ('Fase FRF (grados) '), xlabel ('Frecuencia (Hz)')

   Ejecute este script en su computadora y envíe las gráficas que produce. Adicionalmente,

   1. calcular la frecuencia de interrupción\(f_{b}=1 /\left(2 \pi \tau_{1}\right)\) y mostrar que coincide con la frecuencia de ruptura inferida de las gráficas de MATLAB;
   2. usar aritmética compleja para evaluar a mano (y calculadora manual) el FRF complejo\(F R F(\omega)=\frac{1}{1+j \omega \tau_{1}}\), a frecuencia\(f\) = 30 Hz, y mostrar que su relación de magnitud calculada a mano y fase coinciden con las de MATLAB. Es posible que tenga ocasión de hacer más gráficos de FRF, así que, para su referencia futura, asegúrese de comprender las operaciones de todos los comandos de MATLAB en el script anterior.
4. La ODE gobernante del filtro paso alto amortiguador-resorte serie en la Figura 3.7.4 es la Ecuación 3.7.6,\(\dot{x}_{o}+\left(1 / \tau_{1}\right) x_{o}=\dot{x}_{i}(t)\) [ver también tarea Problema 3.7].
   1. ^{Mostrar que la función de frecuencia-respuesta compleja de filtro paso alto de primer orden asociada es\(F R F(\omega)=j \omega \tau_{1} /\left(1+j \omega \tau_{1}\right)\).}
   2. Para la respuesta de frecuencia, estamos evaluando la entrada en el formulario\(x_{i}(t)=X_{i} \cos \omega t\) y la salida en el formulario\(x_{o}(t)=X_{o} \cos (\omega t+\phi)\). Utilice la FRF de la parte 4.1 para mostrar que las ecuaciones para la relación de magnitud y fase de FRF son\[\frac{X_{o}(\omega)}{X_{i}}=\frac{\omega \tau_{1}}{\sqrt{1+\left(\omega \tau_{1}\right)^{2}}}, \quad \phi(\omega)=\frac{\pi}{2}-\tan ^{-1}\left(\omega \tau_{1}\right)=\tan ^{-1}\left(\frac{1}{\omega \tau_{1}}\right) \nonumber \] Utilice esta ecuación de relación de magnitud para derivar ecuaciones para las asíntotas de baja frecuencia y alta frecuencia, y esbozar esas asíntotas en una gráfica logarítmica como la Figura 4.3.3. Se puede utilizar la definición de frecuencia de ruptura,\(\omega_{b}=1 / \tau_{1}\), para que\(\omega \tau_{1}=\omega / \omega_{b}=f / f_{b}\). Este sistema tiene el carácter de un filtro de paso alto suave, por lo que su boceto de las asíntotas debe tener la apariencia apropiada a ese nombre.
   3. Deje que la constante de tiempo\(\tau_{1}\) = 1 s, y considere el rango de frecuencia de excitación 0.01\(\leq\)\(\omega\)\(\leq\) 100 rad/s (10 ^-2\(\leq\)\(\omega\)\(\leq\) 10 ⁺² rad/s). Adaptar el programa MATLAB, y utilizar el formato gráfico proporcionado en la tarea Problema 4.3 para graficar con MATLAB la relación de magnitud FRF y fase (en grados). Como se hace en el Problema 4.3, programa directamente el FRF complejo, en este caso\(F R F(\omega)=j \omega \tau_{1} /\left(1+j \omega \tau_{1}\right)\), no las ecuaciones de la parte 4.4.3.
5. Un sistema LTI estándar de masa-amortiguador-resorte tiene la ecuación diferencial ordinaria de movimiento\(m \ddot{x}+c \dot{x}+k x=f_{x}(t)\), en la que\(f_{x}(t)\) está la entrada y\(x(t)\) es la salida.
   1. Utilice la ODE para derivar la función de transferencia\(T F(s) \equiv L[x(t)]_{I C s=0} / L\left[f_{x}(t)\right]\) para el\(k\) sistema\(m\)\(c\) - -. Esta función de transferencia es una ecuación algebraica en términos de variables independientes\(s\) y constantes\(m\),\(c\), y\(k\).
   2. Utilice la función de transferencia\(TF(s)\) para derivar la función de respuesta de frecuencia compleja\(FRF(\omega)\) para el\(k\) sistema\(m\)\(c\) - - en términos de frecuencia variable independiente\(\omega\) y constantes\(m\),\(c\), y\(k\).
   3. A partir\(FRF(\omega)\) del\(k\) sistema\(m\)\(c\) - -, escribir ecuaciones en términos de frecuencia\(\omega\) y constantes variables independientes\(m\)\(c\), y\(k\) para la relación de magnitud real\(|F R F(\omega)|\) y el ángulo de fase real\(\angle F R F(\omega)=\phi(\omega)\).