6.3: Ejemplos de respuesta del sistema de primer orden

Ejemplo\(\PageIndex{1}\)

A menudo es el caso de que la entrada a un sistema se describe por diferentes funciones, cada función en efecto durante un período de tiempo diferente para\(t > 0\). Por ejemplo, la siguiente ecuación y dibujo representan una entrada que consta de dos funciones generales diferentes:

\ [u (t) =\ left\ {\ begin {array} {c}
0,\ quad t<0\\
u_ {1} (t),\ quad 0<t<t_ {1}\\
u_ {2} (t),\ quad t_ {1} <t
\ end {array}\ derecha. \ nonumber\]

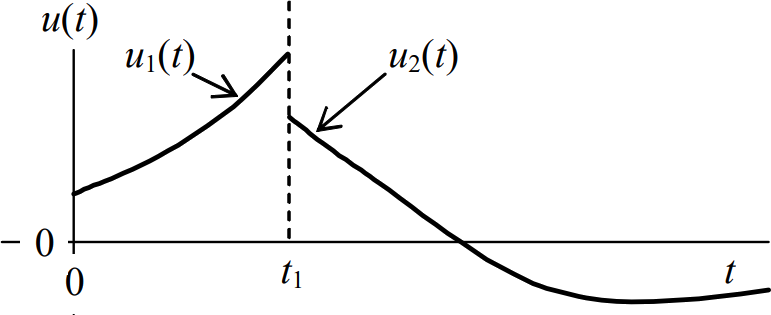
Solución

La respuesta forzada general a este tipo de entrada puede expresarse muy bien en términos de integrales de convolución, pero debemos reconocer que requiere de dos ecuaciones diferentes, y debemos considerar cuidadosamente los límites de las integrales definidas. Primero, para el intervalo de tiempo\(0 \leq t \leq t_{1}\), es claro que la segunda forma de Ecuaciones 6.2.4 es directamente aplicable, con\(u(t) \equiv u_{1}(t)\):

\[x(t)=x_{0} e^{-t / \tau_{1}}+b \int_{\tau=0}^{\tau=t} e^{-(t-\tau) / \tau_{1}} u_{1}(\tau) d \tau \quad, \text { for } 0 \leq t \leq t_{1}\label{eqn:6.6a} \]

Para la respuesta durante el segundo intervalo de tiempo,\(t \geq t_{1}\), la integral definida en la segunda forma de Ecuaciones 6.2.4 aún debe evaluarse sobre los límites\(\tau=0\) a\(\tau=t>t_{1}\), lo que significa que ambos\(u_{1}\) y\(u_{2}\) necesitan ser integrados, pero cada uno solo sobre el intervalo de tiempo para el que se define:

\[x(t)=x_{0} e^{-t / \tau_{1}}+b\left[\int_{\tau=0}^{\tau=t_{1}} e^{-(t-\tau) / \tau_{1}} u_{1}(\tau) d \tau+\int_{\tau=t_{1}}^{\tau=t} e^{-(t-\tau) / \tau_{1}} u_{2}(\tau) d \tau\right] \quad, \text { for } t \geq t_{1}\label{eqn:6.6b} \]

\(\ref{eqn:6.6b}\)Obsérvese especialmente en Ecuación que\(\tau=t_{1}\) es tanto el límite superior de la integral que implica\(u_1\) como el límite inferior de la integral que implica\(u_2\). Las ecuaciones\(\ref{eqn:6.6a}\) y\(\ref{eqn:6.6b}\) son especialmente útiles para la respuesta a un pulso de duración limitada, como se ilustra en el siguiente ejemplo.

Ejemplo\(\PageIndex{2}\)

Consideramos nuevamente el problema de velocidad de una masa que se mueve sobre una película viscosa, que se resuelve mediante métodos básicos de ODE en la Sección 1.5:

\[\mathrm{ODE}+\mathrm{IC}: m \dot{v}+c v=f_{x}(t), \quad v(0)=v_{0}, \quad \text { find } v(t) \text { for } t>0\label{eqn:6.7} \]

\ [f_ {x} (t) =\ izquierda\ {\ comenzar {matriz} {c}
F\ sin\ izquierda (\ pi t/t_ {d}\ derecha)\ equiv F\ sin\ omega t\ quad\ texto {donde}\ omega=\ pi/t_ {d}, 0\ leq t\ leq t_ {d}\
0, t_ {d} <t
\ end {array}\ derecho. \ nonumber\]

Solución

Aquí tenemos\(u(t)=f_{x}(t)\),\(\tau_{1}=m / c\), y\(b=1 / m\). Relativo a la notación del Ejemplo\(\PageIndex{1}\) anterior,\(u_{1}\) es el pulso de medio seno, y\(u_{2}\) es cero.

Mientras el pulso está activo,\(0 \leq t \leq t_{d}\), La ecuación\(\ref{eqn:6.6a}\) se convierte

\[v(t)=v_{0} e^{-t / \tau_{1}}+\frac{F}{m} e^{-t / \tau_{1}} \int_{\tau=0}^{\tau=t} e^{\tau / \tau_{1}} \sin \omega \tau d \tau\label{eqn:6.8} \]

Podemos evaluar la integral definida por varios métodos diferentes: encontrarla en una tabla de integrales definidas (o integrales indefinidas, pero no olvidemos el límite inferior de integración); o integrarla por partes dos veces; o evaluarla con software que haga manipulación simbólica, como Mathematica o versiones recientes de MATLAB. El resultado es

\[\int_{\tau=0}^{\tau=t} e^{\tau / \tau_{\mathrm{t}}} \sin \omega \tau d \tau=\frac{\tau_{1}}{1+\left(\omega \tau_{1}\right)^{2}}\left[e^{t / \tau_{1}}\left(\sin \omega t-\omega \tau_{1} \cos \omega t\right)+\omega \tau_{1}\right]\label{eqn:6.9} \]

Combinando Ecuación\(\ref{eqn:6.8}\) y Ecuación\(\ref{eqn:6.9}\) da la velocidad durante la duración del pulso:

\[v(t)=\left[v_{0}+\frac{F}{c} \frac{\omega \tau_{1}}{1+\left(\omega \tau_{1}\right)^{2}}\right] e^{-t / \tau_{1}}+\frac{F}{c} \frac{1}{1+\left(\omega \tau_{1}\right)^{2}}\left(\sin \omega t-\omega \tau_{1} \cos \omega t\right), 0 \leq t \leq t_{d}\label{eqn:6.10} \]

En el instante\(t=t_{d}\) en que el pulso va a cero\(\omega t_{d}=\pi\),, entonces la velocidad es

\[v\left(t_{d}\right)=\left[v_{0}+\frac{F}{c} \frac{\omega \tau_{1}}{1+\left(\omega \tau_{1}\right)^{2}}\right] e^{-t_{d} / \tau_{1}}+\frac{F}{c} \frac{\omega \tau_{1}}{1+\left(\omega \tau_{1}\right)^{2}}\label{eqn:6.11} \]

Para el tiempo después de que el pulso va a cero,\(t_{d} \leq t\), Ecuación\(\ref{eqn:6.6b}\) se convierte

\[v(t)=v_{0} e^{-t / \tau_{1}}+\frac{F}{m} e^{-t / \tau_{1}}\left(\int_{\tau=0}^{\tau=t_{d}} e^{\tau / \tau_{1}} \sin \omega \tau d \tau+\int_{\tau=t_{d}}^{\tau=t} e^{\tau / \tau_{1}} \times 0 d \tau\right)\label{eqn:6.12} \]

Con el uso de nuevo de la ecuación\(\ref{eqn:6.9}\), y de algún álgebra, la ecuación\(\ref{eqn:6.12}\) se convierte

\[v(t)=v_{0} e^{-t / \tau_{1}}+\frac{F}{c} e^{-t / \tau_{1}} \frac{\omega \tau_{1}}{1+\left(\omega \tau_{1}\right)^{2}}\left(1+e^{t_{d} / \tau_{1}}\right)=v\left(t_{d}\right) e^{-\left(t-t_{d}\right) / \tau_{1}}, \text { for } t \geq t_{d}\label{eqn:6.13} \]

La forma final en el lado derecho de la Ecuación\(\ref{eqn:6.13}\) usa Ecuación\(\ref{eqn:6.11}\), y muestra que la respuesta post-pulso es una decadencia exponencial pura, que esperaríamos físicamente.

Ejemplo\(\PageIndex{3}\)

De la Sección 3.3, tenemos la ecuación de movimiento para la velocidad\(p(t)\) de giro de una rueda de reacción Figura 3.3.1 con inercia rotacional\(J\)\(c_{\theta}\), constante de amortiguación viscosa del rodamiento y par motor aplicado\(M_{m}(t)\):

\[\dot{p}+\frac{c_{\theta}}{J} p=\frac{1}{J} M_{m}(t) \Rightarrow \dot{p}+\frac{1}{\tau_{1}} p=b M_{m}(t) \text { where } \tau_{1}=\frac{J}{c_{\theta}} \text { and } b=\frac{1}{J} \nonumber \]

Solución

Que la velocidad inicial sea cero,\(p(0) \equiv p_{0}=0\). Deje que el par motor tenga la forma de una rampa:

\[M_{m}(t)=\frac{M_{r}}{t_{r}} t, t \geq 0 \nonumber \]

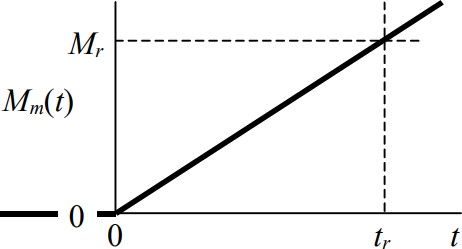
Entonces la segunda forma de solución general Ecuaciones 6.2.4 se convierte

\[p(t)=p_{0} e^{-t / \tau_{1}}+b \int_{\tau=0}^{\tau=t} e^{-(t-\tau) / \tau_{1}} M_{m}(\tau) d \tau=\frac{1}{J} \int_{\tau=0}^{\tau=t} e^{-(t-\tau) / \tau_{1}} \frac{M_{r}}{t_{r}} \tau d \tau \nonumber \]

\[\Rightarrow \quad p(t)=\frac{1}{J} \frac{M_{r}}{t_{r}} e^{-t / \tau_{1}} \int_{\tau=0}^{\tau=t} e^{\tau / \tau_{1}} \tau d \tau \nonumber \]

Podemos evaluar la integral fácilmente utilizando la integración por partes:

\[\int_{\tau=0}^{\tau=t} \overbrace{\tau}^{u} \overbrace{e^{\tau / \tau_{1}}}^{d v} d \tau=\left[\tau \times \tau_{1} e^{\tau / \tau_{1}}\right]_{\tau=0}^{\tau=t}-\int_{\tau=0}^{\tau=t} \tau_{1} e^{\tau / \tau_{1}} d \tau=\tau_{1} t e^{t / \tau_{1}}-\tau_{1}^{2}\left(e^{t / \tau_{1}}-1\right) \nonumber \]

Por lo tanto, la solución total es

\[p(t)=\frac{1}{J} \frac{M_{r}}{t_{r}} e^{-t / \tau_{1}}\left[\tau_{1} t e^{t / \tau_{1}}-\tau_{1}^{2}\left(e^{t / \tau_{1}}-1\right)\right]=\frac{M_{r}}{c_{\theta} t_{r}}\left[t-\tau_{1}\left(1-e^{-t / \tau_{1}}\right)\right]\label{eqn:6.14} \]

Al esbozar una gráfica versus el tiempo de la velocidad de giro adimensional\(\frac{p(t)}{M_{r} / c_{\theta}}\), puede mostrar fácilmente que\(t \rightarrow \infty\), ya que esta cantidad es asintótica a la función de rampa\(\left(t-\tau_{1}\right) / t_{r}\).