6.5: Algoritmo Numérico para la Solución General del Problema Estándar de Primer Orden

Buscamos soluciones de la Ecuación 6.4.5 en forma de series temporales, es decir, en instantes discretos e igualmente espaciados en el tiempo. En consecuencia, definimos la siguiente notación que emplea subíndices descriptivos:

\(t=\)	\(t_1\)	\(t_{2}=t_{1}+\Delta t\)	\(t_{3}=t_{2}+\Delta t\)	\(\dots\)	\(t_{n}=t_{n-1}+\Delta t\)	\(t_{n+1}=t_{n}+\Delta t\)	\(\dots\)
\(x(t)=\)	\(x_1\)	\(x_2\)	\(x_3\)	\(\dots\)	\(x_{n}\)	\(x_{n+1}\)	\(\dots\)
\(u(t)=\)	\(u_1\)	\(u_2\)	\(u_3\)	\(\dots\)	\(u_{n}\)	\(u_{n+1}\)	\(\dots\)

Conceptualmente, comenzamos con los valores conocidos en\(t = t_1\), luego integramos la Ecuación 6.4.5 de\(t_{1}\) a\(t_{2}=t_{1}+\Delta t\), en la que definimos\(\Delta t\) como el paso de tiempo constante; ahora tenemos valores conocidos en\(t=t_{2}\), así podemos integrarnos nuevamente para pasar de\(t_{2}\) a\(t_{3}=t_{2}+\Delta t\). Procedemos de esta manera de una vez a la siguiente hasta que hayamos determinado valores de\(x(t)\) en instantes discretos en el tiempo a lo largo del intervalo de tiempo completo de interés. De la Ecuación 6.4.5, la ecuación exacta y general para pasar del instante de tiempo\(t_{n-1}\) al siguiente instante\(t_n\) es

\[x_{n}=e^{a\left(t_{n}-t_{n-1}\right)} x_{n-1}+\int_{\tau=t_{n-1}}^{\tau=t_{n}} e^{a\left(t_{n}-\tau\right)} b u(\tau) d \tau\label{eqn:6.18} \]

Al comparar la Ecuación\(\ref{eqn:6.18}\) con la Ecuación 6.2.4, observe que la integral en la Ecuación\(\ref{eqn:6.18}\) es claramente una integral de convolución de respuesta forzada.

Hasta este punto, la solución es exacta. Pero ahora introducimos lo que, en general, es una aproximación. Suponemos que\(u(\tau)\) varía tan poco a lo largo del paso de tiempo de integración\(\Delta t\) que introduce solo un pequeño error para aproximarse\(u(\tau)\) como constante sobre\(\Delta t\), permaneciendo su valor que al inicio del tiempo de integración:

\[u(\tau) \approx u\left(t_{n-1}\right) \equiv u_{n-1} \text { for } t_{n-1} \leq \tau<t_{n}\label{eqn:6.19} \]

Usando la ecuación de aproximación\(\ref{eqn:6.19}\) y\(t_{n}=t_{n-1}+\Delta t\), reescribimos la ecuación\(\ref{eqn:6.18}\) con la integral de convolución expresada en una forma más fácilmente integrable:

\[x_{n}=e^{a \Delta t} x_{n-1}+\left[\int_{\tau=t_{n-1}}^{\tau=t_{n-1}-\Delta t} e^{a\left(t_{n-1}+\Delta t-\tau\right)} d \tau\right] b u_{n-1} \nonumber \]

Cambiamos la variable de integración,\(\xi=t_{n-1}+\Delta t-\tau\), para que la integral se convierta

\[\int_{\xi=\Delta t}^{\xi=0} e^{a \xi}(-d \xi)=\int_{\xi=0}^{\xi=\Delta t} e^{a \xi} d \xi=\frac{1}{a}\left(e^{a \Delta t}-1\right) \nonumber \]

Finalmente, con la ecuación de aproximación\(\ref{eqn:6.19}\), la ecuación de solución se\(\ref{eqn:6.18}\) puede escribir como

\[x_{n}=e^{a \Delta t} x_{n-1}+\frac{1}{a}\left(e^{a \Delta t}-1\right) b u_{n-1} \equiv \phi x_{n-1}+\gamma u_{n-1}\label{eqn:6.20} \]

\(\ref{eqn:6.20}\)La ecuación es una fórmula de recurrencia que es fácil de evaluar numéricamente de un instante de tiempo al siguiente, especialmente porque los coeficientes\(\phi \equiv e^{a \Delta t}\) y\(\gamma \equiv\left(e^{a \Delta t}-1\right) b / a=(\phi-1) b / a\) son invariantes\(\Delta t\) una vez seleccionados. Tenga en cuenta que si la entrada\(u(t)\) es una constante, como para una función de paso, entonces\(u_{n}=\) constante para todos\(n=1,2, \ldots\), en cuyo caso Ecuación\(\ref{eqn:6.20}\) es una solución exacta porque la ecuación\(\ref{eqn:6.19}\) es exacta, no una aproximación. Además, si el real\(u(t)\) es constante por partes, entonces la Ecuación se\(\ref{eqn:6.20}\) puede aplicar para producir resultados exactos, siempre que\(\Delta t\) se elija individualmente para cada intervalo de constante de\(u(t)\) tal manera que el intervalo sea un múltiplo entero propio\(\Delta t\).

Para ilustrar la aplicación de la Ecuación\(\ref{eqn:6.20}\), volvemos a visitar la solución numérica de la Sección 1.6, la respuesta de velocidad de un sistema amortiguador de masa a un pulso de fuerza de medio seno. M-archivo MatlabDEMO11.m de la Sección 1.6, que calcula exactamente la respuesta, proporciona el punto de referencia para evaluar el cálculo aproximado de la respuesta. El archivo M de script MATLAB para calcular y graficar la respuesta aproximada es:

%Matlabdemo61.m

% de respuesta aproximada del sistema amortiguador de masa al forzamiento de pulso de medio seno IC +

m=5; c=2;% de masa del sistema y coeficiente de amortiguación viscoso, unidades SI

a=-c/m; b=1/m;

F=18; td=7.5;% de pulso de medio seno, amplitud (N), duración (s) del pulso

w=pi/td; %frecuencia circular del pulso de medio seno (rad/s)

Dt=1.5; %paso de tiempo para cálculos de recurrencia

t=0:dt:24; lt=length (t); %array de instantes de tiempo para cálculos de recurrencia

phi=exp (a*dt); gam =( phi-1) /a*b;% constantes en la fórmula de recurrencia

para N=1:LT %serie de tiempo array de pulso de fuerza de entrada

si t (n) <=7.5

fx (n) =F*sin (pi*t (n) /td);

else

fx (n) =0;

final

final

v=ceros (1, Lt); v (1) =3.3; %matriz de velocidad de inicialización, velocidad inicial (m/s)

para n=2:lt

v (n) =phi*v (n-1) +gam*fx (n-1);

final

parcela (t, v, 'k'), barra (t+dt/2, fx/10,1, 'k')

Tenga en cuenta que la implementación de la fórmula de recurrencia Ecuación\(\ref{eqn:6.20}\) en MatlabDemo61.m es un simple de tres líneas for -loop.

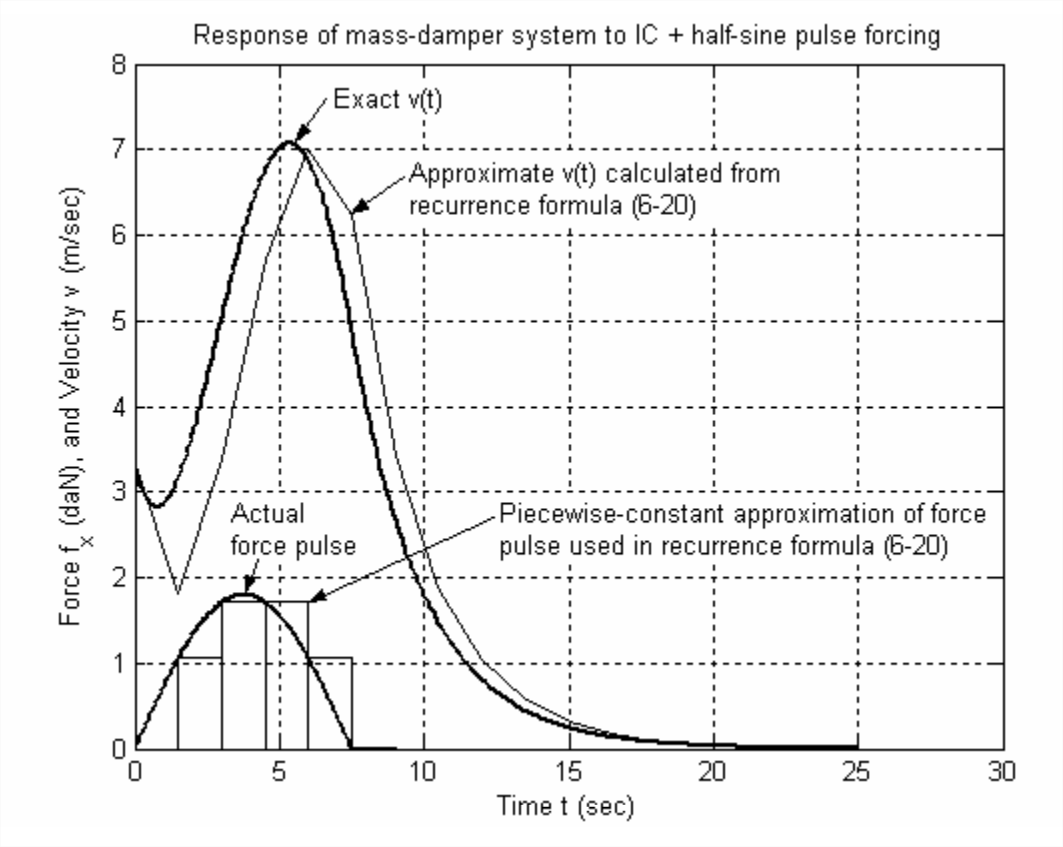
La figura de la página siguiente se produjo combinando los resultados de los archivos M MatlabDemo11.m y MatlabDemo61.m, y luego agregando etiquetas explicativas y editando la gráfica de barras. Para este ejemplo, el paso de tiempo\(\Delta t\) se eligió intencionalmente para que fuera irrazonablemente grande,\(\Delta t\) = 1.5 s (comparado con la constante de tiempo del sistema\(\tau_{1}\) = 2.5 s), con el fin de producir claras distinciones entre las variables dinámicas exactas y aproximadas. Sin embargo, el cálculo aproximado de la velocidad muestra las tendencias correctas cualitativamente y no es altamente inexacto cuantitativamente. Si los cálculos se repitieran con un paso de tiempo más razonable\(\Delta t \leq 0.1 \tau_{1}\), entonces los resultados serían mucho más precisos (tarea Problema 6.4).

Observe también en la figura de la siguiente página el gráfico de barras de la fuerza aproximada\(f_{x}(t)\) utilizada en la Ecuación\(\ref{eqn:6.20}\), que es la representación gráfica de la ecuación de aproximación\(\ref{eqn:6.19}\). Debido a su carácter constante a trozos, a esto a veces se le llama aproximación de escalera. Esta aproximación introduce un retardo de tiempo o retraso en el orden de\(\Delta t\) en la entrada aproximada. Este retardo de tiempo artificial se transmite obviamente a la respuesta aproximada calculada.

Figura\(\PageIndex{1}\)

Es interesante y posiblemente útil observar que, debido a aproximarse\(u(\tau)\) como constante a lo largo de cada paso de tiempo\(\Delta t\), la Ecuación\(\ref{eqn:6.20}\) es esencialmente IC + respuesta de paso sobre cada uno\(\Delta t\). Supongamos que íbamos a buscar una fórmula de recurrencia aún más precisa que la ecuación\(\ref{eqn:6.20}\) aproximándose\(u(\tau)\) como variando linealmente con el tiempo en cada paso de tiempo. En ese caso, la solución sería esencialmente IC + respuesta escalonada + respuesta rampa sobre cada uno\(\Delta t\). (El Ejemplo 6.3 en la Sección 6.3 ilustra la respuesta en rampa). Entonces, la fórmula de recurrencia aproximada más refinada sería Ecuación\(\ref{eqn:6.20}\) complementada con un término adicional que represente la respuesta en rampa, y esperaríamos que ese término adicional incluyera ambos\(u_{n-1}\) y\(u_{n}\) como consecuencia de la variación lineal aproximada de\(u(\tau)\); ver tarea Problema 6.5.