10.6: Respuesta batiente de sistemas de segundo orden a excitación sinusoidal aplicada súbitamente

Hasta ahora en el Capítulo 10, hemos considerado solo la respuesta de frecuencia pura de los sistemas ^{de segundo} orden, es decir, la respuesta sinusoidal en estado estacionario a la excitación sinusoidal. En el análisis de frecuencia-respuesta basado en la Ecuación 4.7.18, se ignoran las condiciones iniciales, al igual que cualquier parte de arranque sinusoidal no estable de la excitación; en otras palabras, tanto la excitación sinusoidal pura como la respuesta son idealizadas para comenzar en algún tiempo indefinido en el pasado. Pero cualquier excitación real debe comenzar en algún momento definido, momento en el que cualquier sistema dinámico real tiene algunas condiciones iniciales. Después del inicio de la excitación sinusoidal, habrá un intervalo de transición de respuesta entre las condiciones iniciales y, siempre que el sistema sea estable, el logro de la respuesta sinusoidal en estado estacionario. La Sección 4.2 ilustra dicho intervalo de transición para un sistema estable ^de primer orden, que no presenta un comportamiento oscilatorio natural. En esta sección, consideramos una forma de respuesta transicional, batido, que a menudo se observa en sistemas vibratorios ligeramente amortiguados, cuyas formas más simples son los sistemas de ^segundo orden subamortiguados.

El carácter básico de la respuesta de latido a la excitación sinusoidal se ilustra mejor teóricamente por el sistema idealizado de ^segundo orden sin amortiguar. Consideremos nuevamente la ODE estándar para sistemas de ^{segundo orden sin} amartillar, Ecuación 10.1.1. Supongamos ahora que\(u(t)=0\) para\(t < 0\), y definamos la excitación sinusoidal aplicada súbitamente (SAS) como\(u(t)=U \sin \omega t\) para\(t\geq 0\). (Usamos\(\sin \omega t\) aquí más que lo habitual\(\cos \omega t\) porque es más natural, especialmente para los sistemas mecánicos, que la excitación comience continuamente desde cero a\(t\) = 0, en lugar de con una discontinuidad). Así, la ecuación 10.1.1 de la ODE se convierte

\[\ddot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)=\omega_{n}^{2} U \sin \omega t, \text { for } t \geq 0\label{eqn:10.36} \]

Por simplicidad, dejamos que las condiciones iniciales sean cero:\(\dot{x}(0)=0\) y\(x(0)=0\). La solución algebraica completa de la Ecuación ODE\(\ref{eqn:10.36}\) con estos CI de descanso se encuentra en la tarea Problema 1.12 por el método de coeficientes indeterminados:

\[x(t)=\frac{U}{1-\left(\omega / \omega_{n}\right)^{2}}\left[\sin \omega t-\left(\omega / \omega_{n}\right) \sin \omega_{n} t\right], \text { valid for } \omega \neq \omega_{n}, t \geq 0\label{eqn:10.37} \]

La ecuación\(\ref{eqn:10.37}\) es válida sólo si la frecuencia de excitación es diferente a la frecuencia natural,\(\omega \neq \omega_{n}\); sin embargo, esto no es una restricción práctica seria, porque en realidad es casi imposible excitar un sistema exactamente a su frecuencia natural. [Pero ver tarea Problema 1.12.4 para la solución teórica válida si\(\omega=\omega_{n}\).]

Es apropiado escribir la ecuación de solución de respuesta\(\ref{eqn:10.37}\) en una forma algebraica ligeramente diferente:

\[x(t)=\frac{U}{1-\left(\omega / \omega_{n}\right)^{2}}\left[\sin \omega t-\sin \omega_{n} t+\left(1-\omega / \omega_{n}\right) \sin \omega_{n} t\right]\label{eqn:10.38} \]

Esta forma de nos\(x(t)\) permite invocar una identidad trigonométrica útil:

\[\sin \omega t-\sin \omega_{n} t=2 \cos \frac{1}{2}\left(\omega t+\omega_{n} t\right) \times \sin \frac{1}{2}\left(\omega t-\omega_{n} t\right)\label{eqn:10.39} \]

Ahora podemos expresar la solución Ecuación\(\ref{eqn:10.38}\) en una ecuación que muestra más claramente las características del latido:

\[x(t)=\frac{U}{1-\left(\omega / \omega_{n}\right)^{2}}\left[2 \cos \frac{1}{2}\left(\omega+\omega_{n}\right) t \times \sin \frac{1}{2}\left(\omega-\omega_{n}\right) t+\left(1-\omega / \omega_{n}\right) \sin \omega_{n} t\right]\label{eqn:10.40} \]

Para el cálculo, con definiciones de relación de frecuencia de conducción\(\beta \equiv \omega / \omega_{n}\) y periodo natural\(T_{n} \equiv 2 \pi / \omega_{n}\), expresamos Ecuación\(\ref{eqn:10.40}\) en la forma adimensional:

\[\frac{x(t)}{U}=\frac{1}{1-\beta^{2}}\left[2 \cos \left((\beta+1) \pi \frac{t}{T_{n}}\right) \times \sin \left((\beta-1) \pi \frac{t}{T_{n}}\right)+(1-\beta) \sin \left(2 \pi \frac{t}{T_{n}}\right)\right]\label{eqn:10.41} \]

Usemos la evaluación numérica y la visualización gráfica para ayudarnos a examinar las partes de Ecuaciones\(\ref{eqn:10.40}\) y\(\ref{eqn:10.41}\); La figura\(\PageIndex{1}\) de la siguiente página incluye gráficas tanto de excitación sinusoidal aplicada repentinamente como de la respuesta asociada calculada a partir de la ecuación\(\ref{eqn:10.41}\), con la excitación frecuencia establecida en 90% de la frecuencia natural,\(\omega=0.9 \omega_{n}\) o\(\beta=0.9\).

Con el uso de Figura\(\PageIndex{1}\), podemos identificar los roles de los términos entre corchetes de Ecuaciones\(\ref{eqn:10.40}\) y\(\ref{eqn:10.41}\) para cualquier caso en el que la frecuencia de excitación\(\omega\) esté algo cercana a la frecuencia natural del sistema\(\omega_{n}\). El término dominante (en magnitud) que se asemeja mucho a la excitación es\(2 \cos \frac{1}{2}\left(\omega+\omega_{n}\right) t\), una sinusoide cuya frecuencia es la media de la excitación y frecuencias naturales. Pero este término dominante se multiplica por\(\sin \frac{1}{2}\left(\omega-\omega_{n}\right) t\), que es un modulador de amplitud que varía lentamente cuya frecuencia es la mitad de la diferencia entre las frecuencias de excitación y naturales. Para el caso de Figura\(\PageIndex{1}\) con\(\omega / \omega_{n}=0.9\), tenemos\(\left|\frac{1}{2}\left(\omega-\omega_{n}\right)\right|=0.05 \omega_{n}\). Por lo tanto, el periodo completo del término de modulación de amplitud es\(2 \pi / 0.05 \omega_{n}=20 T_{n}\); a partir de la Figura\(\PageIndex{1}\), este periodo es el intervalo total entre el tiempo\(t = 0\) s y el segundo mínimo posterior de la envolvente moduladora de amplitud. Además, los términos de latido son mínimos en amplitud en cada medio período del término de modulación de amplitud, en este caso\(0,10 T_{n}, 20 T_{n}, \ldots\), y los términos de latido son máximos en amplitud en instantes entre los instantes de medio período, en este caso\(5 T_{n}, 15 T_{n}, 25 T_{n}, \ldots\)

Figura\(\PageIndex{1}\): Gráfica superior: excitación (at\(t = 0\)) sinusoidal (SAS) aplicada súbitamente con frecuencia\(\omega=0.9 \omega_{n}\); gráfica inferior: respuesta desde cero condiciones iniciales de un sistema estándar no amortiguado ^{de segundo} orden que tiene frecuencia natural\(\omega_{n}\).

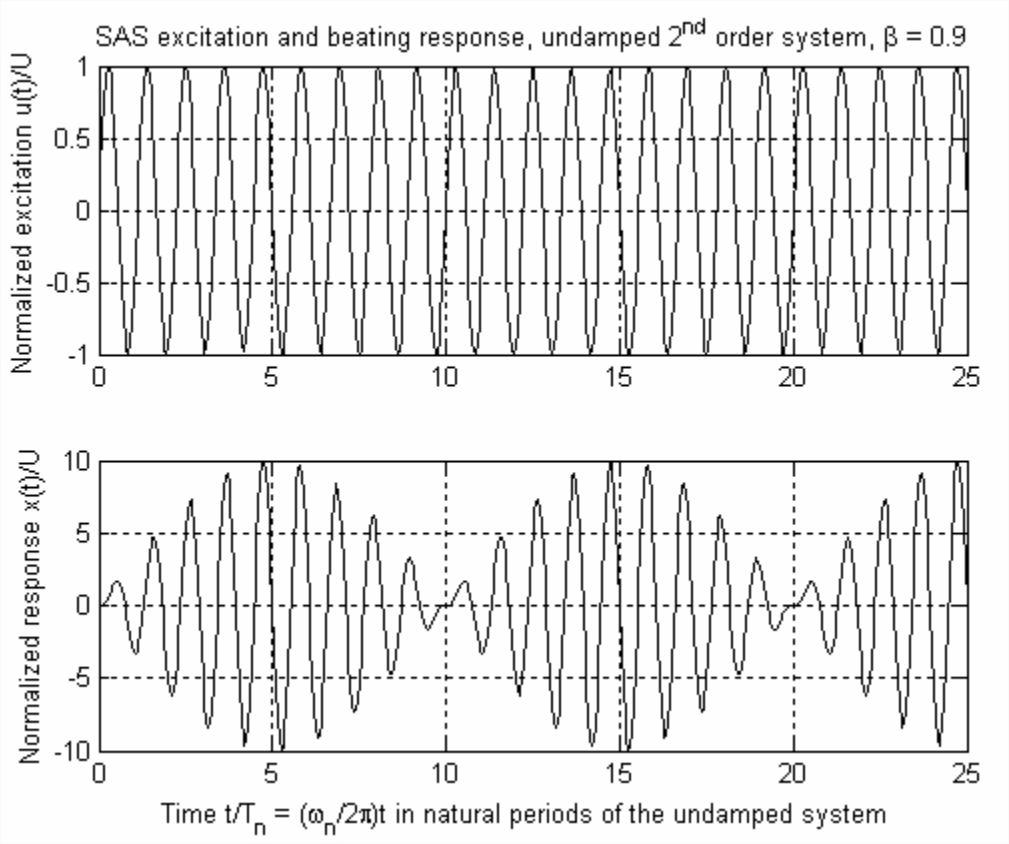
El periodo aparente de latido es el intervalo entre mínimos sucesivos o máximos sucesivos de respuesta,\(10 T_{n}\) en el caso de la Figura\(\PageIndex{1}\), que es la mitad del periodo del término modulador de amplitud. Por lo tanto, la frecuencia aparente de latido es\(\left|\omega-\omega_{n}\right|\), que es el doble de la frecuencia del término modulador de amplitud. De igual manera, cuando escuchamos dos tonos musicales de tonos (frecuencias) cercanos pero no idénticos, la frecuencia de latido que percibimos es la diferencia entre las dos frecuencias tonales.

Consideremos ahora el término restante,\(\left(1-\omega / \omega_{n}\right) \sin \omega_{n} t\), dentro de los paréntesis de Ecuaciones\(\ref{eqn:10.40}\) y\(\ref{eqn:10.41}\). El latido puro sin amortiguar, en general, es la combinación de dos sinusoides que tienen frecuencias diferentes pero muy próximas, ya que las dos sinusoides pasan dentro y fuera de fase entre sí. El batido del sistema de ^segundo orden no amortiguado que se muestra en la Figura\(\PageIndex{1}\) es la combinación de dos sinusoides en el término\(\sin \omega t-\sin \omega_{n} t\) de Ecuación\(\ref{eqn:10.38}\). Estas dos sinusoides representan

1. la respuesta impulsada del sistema a la frecuencia de excitación\(\omega\), y
2. la mayor parte de la respuesta de vibración libre del sistema a su frecuencia natural\(\omega_{n}\).

Cuando estas dos sinusoides están en fase, se combinan y, junto con el menor aporte del término\(\left(1-\omega / \omega_{n}\right) \sin \omega_{n} t\), forman la respuesta máxima; cuando están desfasadas, se anulan entre sí por completo, dejando solo la pequeña parte restante de la respuesta de vibración libre debido al término\(\left(1-\omega / \omega_{n}\right) \sin \omega_{n} t\).

Hasta ahora, hemos examinado la respuesta a la excitación sinusoidal aplicada súbitamente de un sistema físicamente poco realista de ^{segundo orden sin} amortiguar. Consideremos a continuación la influencia de una amortiguación subcrítica más realista al resolver para una respuesta de tiempo completa de un sistema de ^segundo orden subamortiguado el ODE\(\ddot{x}+2 \zeta \omega_{n} \dot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\) con\(u(t) = 0\) para\(t < 0\) y\(u(t)=U \sin \omega t\) para\(t \geq 0\), y con CI de descanso\(x(0)=0\) y\(\dot{x}(0)=0\). Una solución integral de convolución apropiada es la Ecuación 9.3.8:

\[x(t)=\frac{\omega_{n}^{2}}{\omega_{d}} \int_{\tau=0}^{\tau=t} e^{-\zeta \omega_{n} \tau} \sin \omega_{d} \tau \times u(t-\tau) d \tau=\frac{\omega_{n}^{2}}{\omega_{d}} \int_{\tau=0}^{\tau=t} e^{-\zeta \omega_{n} \tau} \sin \omega_{d} \tau \times U \sin \omega(t-\tau) d \tau \nonumber \]

La frecuencia amortiguada es\(\omega_{d} \equiv \omega_{n} \sqrt{1-\zeta^{2}}\), por lo que podemos expresar la respuesta integral en forma adimensional como

\[\frac{x(t)}{U}=\frac{\omega_{n}}{\sqrt{1-\zeta^{2}}} \int_{\tau=0}^{\tau=t} e^{-\zeta \omega_{n} \tau} \sin \omega_{n} \sqrt{1-\zeta^{2}} \tau \times \sin \omega(t-\tau) d \tau\label{eqn:10.42} \]

Después de la evaluación de la formidable integral en Ecuación\(\ref{eqn:10.42}\), la solución es ¹

\[\frac{x(t)}{U}=\frac{e^{-\zeta \omega_{n} t} \beta\left[2 \zeta \cos \omega_{d} t-\frac{\left(1-\beta^{2}-2 \zeta^{2}\right)}{\sqrt{1-\zeta^{2}}} \sin \omega_{d} t\right]+\left(1-\beta^{2}\right) \sin \omega t-2 \zeta \beta \cos \omega t}{\left(1-\beta^{2}\right)^{2}+(2 \zeta \beta)^{2}}\label{eqn:10.43} \]

La ecuación para la respuesta de un sistema de ^segundo orden sin amortiguar que es más similar en forma algebraica a Ecuación\(\ref{eqn:10.43}\) es Ecuación\(\ref{eqn:10.37}\), y se puede mostrar fácilmente que para\(\zeta=0\) Ecuación se\(\ref{eqn:10.43}\) reduce a Ecuación\(\ref{eqn:10.37}\). Sin embargo, a diferencia de la Ecuación\(\ref{eqn:10.37}\), la Ecuación\(\ref{eqn:10.43}\) aparentemente no se puede reconfigurar en una forma comparable a la Ecuación\(\ref{eqn:10.40}\) que sea susceptible de interpretación física relativa al comportamiento de latido. Para aprender el carácter físico de la Ecuación\(\ref{eqn:10.43}\), parece que lo mejor que podemos hacer es evaluarla computacionalmente con parámetros numéricos relevantes y luego interpretar los resultados. Para el cálculo de la Ecuación\(\ref{eqn:10.43}\), con definiciones de relación de frecuencia de conducción\(\beta \equiv \omega / \omega_{n}\) y período natural\(T_{n} \equiv 2 \pi / \omega_{n}\), podemos expresar los argumentos de función dependientes del tiempo de Ecuación\(\ref{eqn:10.43}\) en las siguientes formas en términos de tiempo adimensional\(t / T_{n}\):\(-\zeta \omega_{n} t=-2 \pi \zeta\left(t / T_{n}\right), \omega_{d} t=2 \pi \sqrt{1-\zeta^{2}}\left(t / T_{n}\right)\), y\(\omega t=2 \pi \beta\left(t / T_{n}\right)\). La Figura\(\PageIndex{2}\) incluye gráficas de respuesta SAS calculadas a partir de la Ecuación\(\ref{eqn:10.43}\) para amortiguamiento cero y para relaciones de amortiguamiento viscoso ligero\(\zeta\) = 0.01 y 0.02, con la frecuencia de excitación establecida en 90% de la frecuencia natural,\(\omega=0.9 \omega_{n}\) o\(\beta=0.9\), la misma que para la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{2}\): Cálculos de la ecuación\(\ref{eqn:10.43}\) para un sistema estándar ^{de segundo} orden que tiene frecuencia natural no amortiguada\(\omega_{n}\), con amortiguación cero (arriba) y dos valores positivos de relación de amortiguación viscosa,\(\zeta\) = 0.01 y 0.02; respuesta de las condiciones iniciales de reposo a una aplicada súbitamente ( at\(t\) = 0) excitación sinusoidal (SAS) con frecuencia\(\omega=0.9 \omega_{n}\).

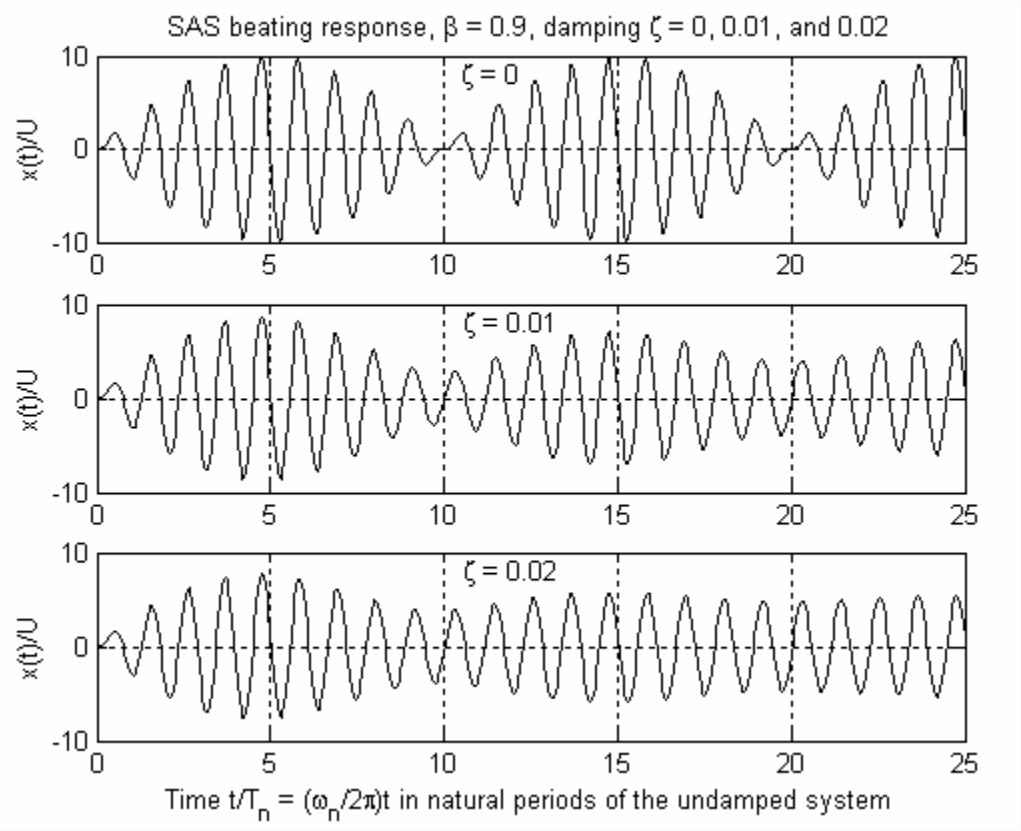
La respuesta en la Figura\(\PageIndex{2}\) para\(\zeta = 0\) es, por supuesto, la misma que la de la Figura\(\PageIndex{1}\), con golpizas muy significativas. Sin embargo, las respuestas para\(\zeta\) = 0.01 y 0.02 muestran que incluso estas cantidades relativamente pequeñas de amortiguamiento suprimen el latido, al menos para este caso de\(\omega=0.9 \omega_{n}\). Aunque menos obvio que para el amortiguamiento cero, el aparente periodo de golpes para\(\zeta=0.01\),\(\sim 10 T_{n}\), sigue siendo bastante evidente. Sin embargo, para\(\zeta=0.02\), la respuesta en la Figura\(\PageIndex{2}\) después de 25 periodos naturales casi se ha asentado en su condición de estado estacionario, para lo cual se puede calcular a partir de la Ecuación 10.2.7 que la relación frecuencia-magnitud de respuesta en estado estacionario es\(X / U=5.171\). Para investigar la naturaleza del latido para cualquier otro caso de relación de amortiguación\(\zeta>0\) y relación de frecuencia de excitación\(\beta \equiv \omega / \omega_{n}\), necesitaríamos nuevamente evaluar la Ecuación\(\ref{eqn:10.43}\) numéricamente; ver, por ejemplo, tarea Problema 10.17.

¹ El autor derivó Ecuación\(\ref{eqn:10.43}\) primero con MATLAB aplicando las operaciones syms, int, simples y bastante simbólicas, y luego implementando el toque humano con lápiz y papel para simplificar aún más el resultado de MATLAB. Ver tarea Problemas 1.6 y 1.9.