11.3: Ejemplos

Ejemplo\(\PageIndex{1}\): damped, spring-supported rigid bar, hinged at point \(H\)

Derivamos la ODE específica de movimiento para el sistema de Figura\(\PageIndex{1}\), asumiendo pequeños ángulos de rotación. La barra tiene inercia rotacional\(J_{H}\) alrededor de la bisagra\(H\), la cual suponemos que tiene una fricción insignificante. La barra se muestra en la posición de equilibrio estático de referencia, sujeta a la gravedad estática pero antes de que la fuerza dinámica aplicada\(F(t)\) se active. El grado dinámico de libertad que\(\theta(t)\) se muestra con líneas discontinuas es la pequeña rotación relativa a la posición de equilibrio estático. (Es la convención gráfica de este libro para este y todos los sistemas posteriores de este tipo que el cuerpo rígido se dibuje en su posición de equilibrio estático, y el movimiento dinámico relativo a esta posición de referencia se indica con líneas discontinuas y anotación). Observe el resorte de rotación con constante de resorte\(k_{\theta}\) en la bisagra\(H\); este resorte resiste la rotación generando un momento opuesto de magnitud\(k_{\theta} \times \theta\). Las unidades típicas para\(k_{\theta}\) son lb-pulgadas/radian y N-m/radian.

Figura\(\PageIndex{1}\): Ejemplo 11.3.1: barra rígida con bisagras amortiguada, soportada por resorte

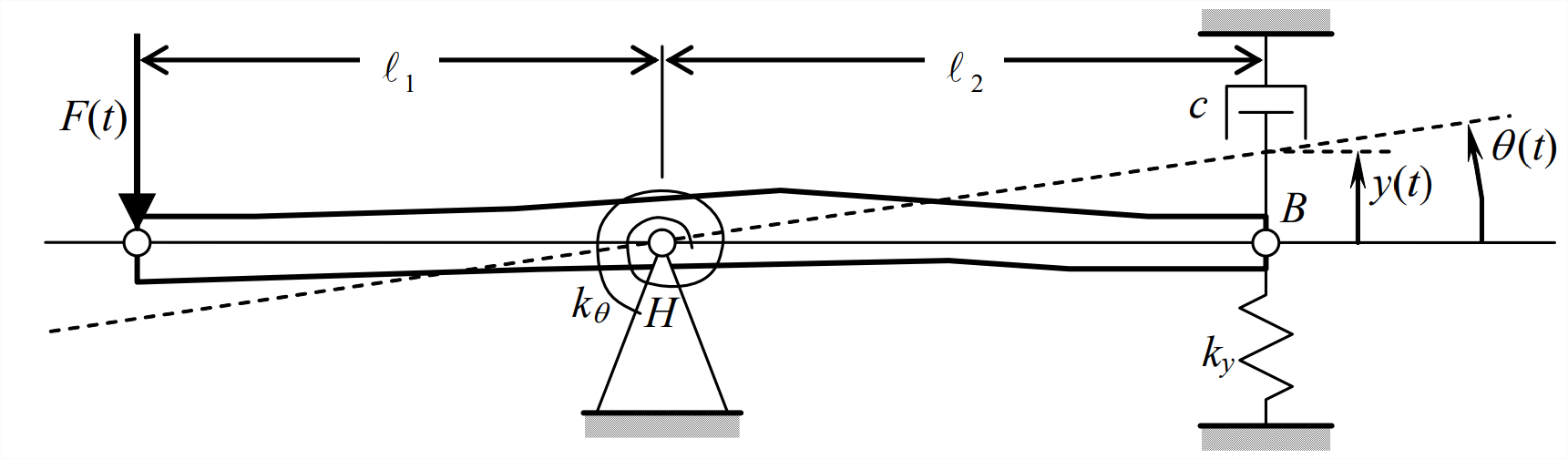
Antes de dibujar un diagrama dinámico de cuerpo libre (DFBD, como se define en la Sección 7.5), necesitamos expresar apropiadamente las fuerzas de reacción sobre la barra en un punto\(B\) desde el resorte de traslación (\(k_{y} \times y\)) y el amortiguador viscoso traslacional (\(c \times \dot{y}\)). Observe que el punto\(B\) se mueve en un arco circular de radio\(\ell_{2}\), así que eso\(y=\ell_{2} \sin \theta\). Para arbitrariamente grandes\(\theta\), el término\(\sin \theta\) y su derivada del tiempo harían que la ecuación de movimiento de la Ecuación 11.2.10 no sea lineal. Sin embargo, la suposición de rotación pequeña\(|\theta(t)|<\approx 10^{\circ}\),, linealiza esa ODE; la geometría de rotación pequeña da ecuaciones lineales aproximadas en términos de\(\theta\) estiramiento\(y\) del resorte de traslación debido al movimiento del punto\(B\), y para la velocidad del amortiguador-pistón \(\dot{y}\):

\[y=\ell_{2} \sin \theta \approx \ell_{2} \theta(\theta \text { in radians }), \quad \text { and } \quad \dot{y}=\ell_{2} \cos \theta \times \dot{\theta} \approx \ell_{2} \dot{\theta} \nonumber \]

La geometría de rotación pequeña se utilizó previamente en el ejemplo de la Sección 7.1 para linealizar la ecuación de movimiento del péndulo. Para el sistema de la Figura\(\PageIndex{1}\), la suposición de rotación pequeña es físicamente plausible así como matemáticamente conveniente, ya que los resortes de traslación y rotación muy probablemente restringirían la rotación de la barra a pequeños ángulos en relación con la posición de equilibrio estático.

El DFBD apropiado se dibuja a continuación. Tenga en cuenta que no incluimos el peso de la barra entre las fuerzas aplicadas. Omitimos el peso de la barra porque solo nos interesa el movimiento dinámico relativo a la posición de equilibrio estático, y porque esta barra es aproximadamente horizontal para que la gravedad no tenga ningún efecto pendular sobre ella; si no estás seguro de por qué descuidamos el peso en este caso, entonces revisa la Sección 7.5.

Figura\(\PageIndex{2}\)

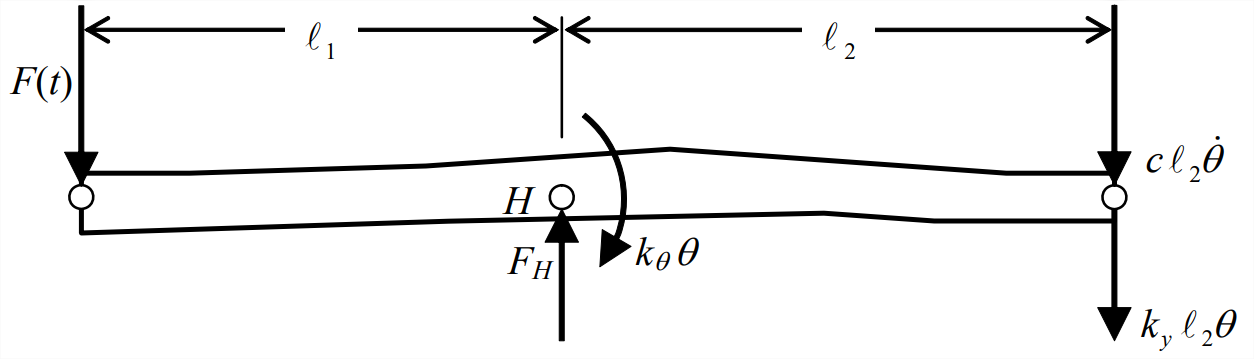
De la DFBD y la Ecuación 11.2.10, la ecuación diferencial ordinaria de movimiento es

\[J_{H} \ddot{\theta}=\ell_{1} F(t)-k_{\theta} \theta-\ell_{2}\left(c \ell_{2} \dot{\theta}+k_{y} \ell_{2} \theta\right) \nonumber \]

\[\Rightarrow \quad J_{H} \ddot{\theta}+c \ell_{2}^{2} \dot{\theta}+\left(k_{\theta}+k_{y} \ell_{2}^{2}\right) \theta=\ell_{1} F(t)\label{eqn:11.12} \]

La ecuación se\(\ref{eqn:11.12}\) puede poner en la forma estándar para un sistema ^{amortiguado de segundo} orden, y todos los resultados relevantes de los Capítulos 9 y 10 pueden expresarse en términos de los parámetros físicos de este sistema mecánico en particular. Por ejemplo, podemos encontrar inmediatamente ecuaciones para el sistema de frecuencia natural no amortiguada y relación de amortiguación viscosa:

\[\omega_{n}=\sqrt{\frac{k_{\theta}+k_{y} \ell_{2}^{2}}{J_{H}}}, \quad 2 \zeta \omega_{n}=\frac{c \ell_{2}^{2}}{J_{H}} \Rightarrow \zeta=\frac{1}{2} \frac{c \ell_{2}^{2}}{\sqrt{J_{H}\left(k_{\theta}+k_{y} \ell_{2}^{2}\right)}}\label{eqn:11.13} \]

NOTA: Es fácil cometer errores en álgebra cuando derivamos resultados como Ecuaciones\(\ref{eqn:11.13}\). Un tipo de verificación parcial bueno y fácil que puedes usar es evaluar las dimensiones físicas de los resultados algebraicos. (Es sólo una comprobación parcial porque la consistencia dimensional es una condición necesaria, pero no garantiza la corrección de una ecuación algebraica). ¿Las ecuaciones\(\ref{eqn:11.13}\) tienen las dimensiones físicas correctas? Deberías poder demostrar que la ecuación para\(\omega_{n}\) tiene la dimensión (tiempo) ^-1 y que la ecuación para\(\zeta\) es adimensional. No hay que olvidar que la rotación\(\theta\) es adimensional y que el radián, la métrica natural de rotación, no tiene unidades. Si se siente más cómodo trabajando con unidades que con dimensiones, es satisfactorio verificar unidades en su lugar. El Cuadro 3.1.1 debería ser útil en relación con las unidades mecánicas.

Ejemplo\(\PageIndex{2}\): 1-DOF typical-section model for study of aerolastic wing twist

Desde el comienzo de la ingeniería aeronáutica moderna a finales del siglo XIX y principios del siglo XX, la interacción de la presión aerodinámica con la flexibilidad estructural del avión a menudo ha producido consecuencias inesperadas y a veces desastrosas. El tema de estos fenómenos se conoció como aeroelasticidad. Durante y después de la Primera Guerra Mundial, las alas monoplanas en voladizo de relación de aspecto alto tendían a ser susceptibles tanto al aleteo aeroelástico, a la vibración no amortiguada que puede escalar a la destrucción del ala y el avión, como a la divergencia aeroelástica, el giro gradual de un ala en, por ejemplo , pull-up de una inmersión ¹. En sus intentos de analizar estos fenómenos aeroelásticos, los primeros ingenieros aeronáuticos utilizaron modelos dinámicos simplificados de bajo grado de libertad de estructuras de alas. La base de estos modelos se llama sección típica: una sección transversal “típica” de un ala recta y sin barrido de alta relación de aspecto se trata aerodinámicamente como una superficie aerodinámica en flujo bidimensional (sin flujo en el sentido de la envergadura), y estructuralmente como un cuerpo rígido soportado por resorte (sin flexión de la viga en el sentido de la envergadura y retorciendo).

El modelo de sección típica más simple es el sistema de un grado de libertad (1-DOF) dibujado en la Figura\(\PageIndex{3}\). Es útil visualizar esto como un modelo físico montado para pruebas en un túnel de viento. Se supone que el eje elástico EA (la bisagra) no tiene fricción, y el resorte de rotación\(k_{\theta}\) representa la rigidez torsional del ala. (El término eje elástico se refiere a la línea a lo largo de la envergadura de un ala recta y sin barrido de alta relación de aspecto alrededor de la cual las secciones del ala giran en el sentido de la cuerda si se impone un momento de torsión puro sobre el ala). Este modelo está destinado principalmente al estudio de la divergencia aeroelástica. La figura\(\PageIndex{3}\) muestra la típica

Figura\(\PageIndex{3}\): Ejemplo 11.3.2: Sección típica de 1-DOF en una corriente de aire

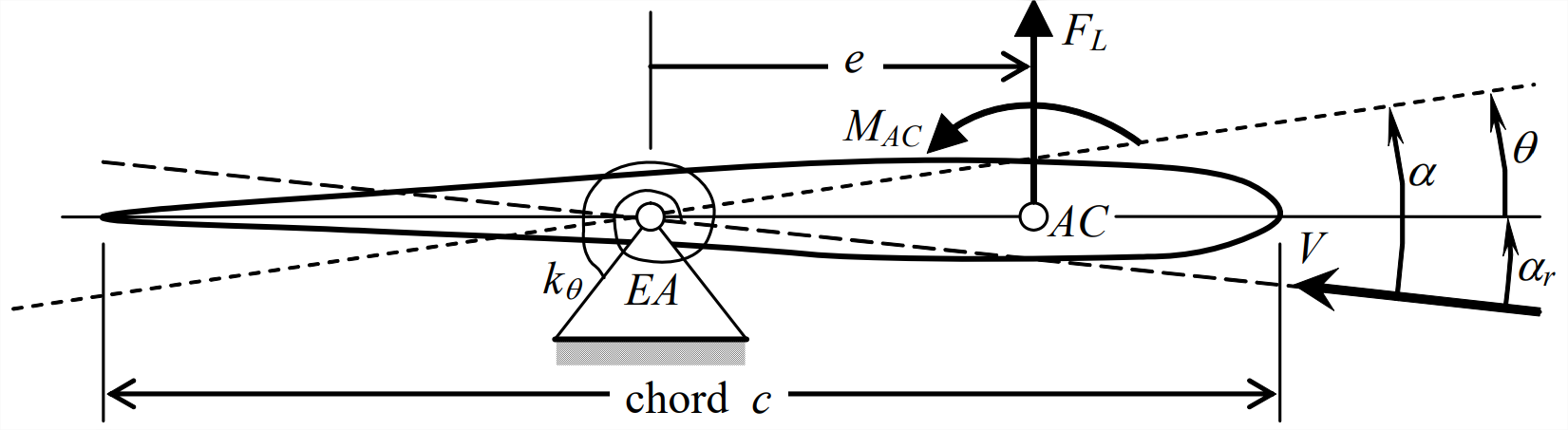
en la posición de equilibrio estático de referencia antes de encender el ventilador del túnel de viento. Al encender el ventilador del túnel de viento se produce una corriente de aire de velocidad de flujo libre constante\(V\) que fluye sobre la sección típica en un pequeño ángulo de incidencia en\(\alpha_{r}\) relación con la línea de cuerda de referencia de la sección típica. La corriente de aire crea una fuerza de elevación resultante\(F_L\) que actúa a través del centro aerodinámico\(AC\), y un momento de cabeceo resultante\(M_{AC}\) que actúa alrededor\(AC\). Para la mayoría de los casos de interés práctico,\(AC\) se adelanta\(EA\) por alguna distancia positiva\(e\), como se muestra en la Figura\(\PageIndex{3}\); la polaridad\(e > 0\) es muy importante en relación con la divergencia. Acciones aerodinámicas\(F_L\) e\(M_{AC}\) imponen momentos sobre el resorte de rotación\(k_{\theta}\), y la flexibilidad del resorte permite la rotación estructural en\(\theta\) relación con la posición de referencia.

El DFBD asociado con la Figura\(\PageIndex{3}\) se dibuja a continuación. La ecuación de movimiento proviene directamente de la DFBD y la Ecuación 11.2.10, con la suposición de pequeños ángulos de incidencia y rotación,\(\left|\alpha_{r}\right|<\approx 10^{\circ}\) y\(|\theta(t)|<\approx 10^{\circ}\), y con\(J_{E A}\) ser la inercia rotacional de la sección típica sobre\(EA\):

\[J_{E A} \ddot{\theta}=F_{L} e+M_{A C}-k_{\theta} \theta \Rightarrow J_{E A} \ddot{\theta}+k_{\theta} \theta=F_{L} e+M_{A C}\label{eqn:11.14} \]

Figura\(\PageIndex{4}\)

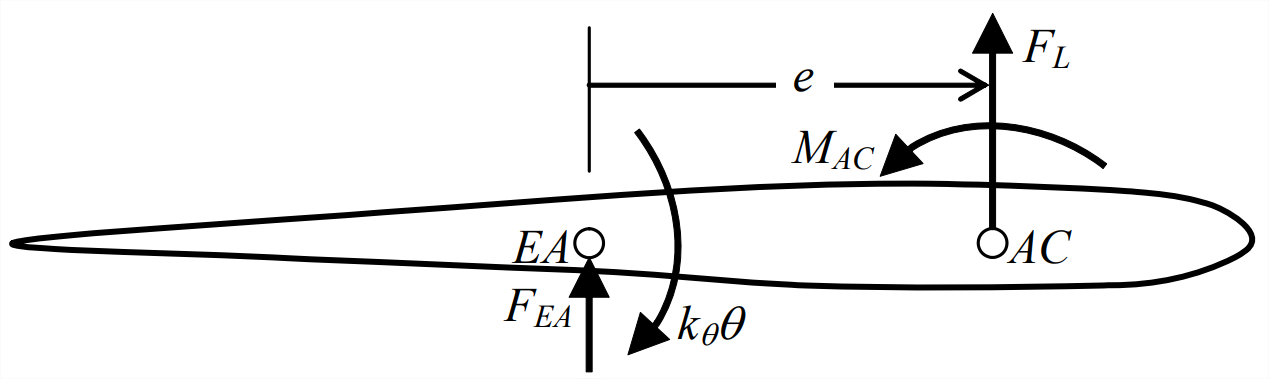
Podemos\(\ref{eqn:11.14}\) convertir Ecuación en una forma más interesante y útil relacionando las acciones aerodinámicas con la rotación estructural. Suponemos que la dirección de la corriente de aire coincide con la actitud de sustentación cero del perfil aerodinámico, es decir, que\(F_L\) sería cero para cualquier valor de velocidad aérea\(V\) si la incidencia del perfil aerodinámico se fijara en\(\alpha_{r}=0\). En consecuencia, el ángulo total de ataque de la superficie aerodinámica con respecto a la actitud de elevación cero es\(\alpha=\alpha_{r}+\theta\). Entonces la elevación aerodinámica y el momento se pueden expresar como

\[F_{L}=\bar{q} S C_{L \alpha} \alpha=\bar{q} S C_{L \alpha}\left(\alpha_{r}+\theta\right), \quad \text { and } \quad M_{A C}=\bar{q} S c C_{M A C}\label{eqn:11.15} \]

Nótese especialmente en Ecuaciones\(\ref{eqn:11.15}\) que una acción aerodinámica (en este caso, elevación\(F_L\)) depende de la deformación estructural (en este caso, rotación\(\theta\)); este tipo de interacción entre aerodinámica y flexibilidad estructural es una característica importante de todos los fenómenos aeroelásticos. Los símbolos utilizados en Ecuaciones\(\ref{eqn:11.15}\) más allá de las previamente definidas son:

\(\bar{q}=\frac{1}{2} \rho V^{2}\)es la presión dinámica de flujo libre (lb/ft ² o N/m ²).

\(\rho\)es la densidad del aire (slug/ft ³ o kg/m ³).

\(S=b c\)es el área de forma plana de la sección típica (ft ² o m ²).

\(b\)es el tramo de la sección típica en el plano del papel (ft o m).

\(C_{L \alpha}>0\)es la pendiente de la curva del coeficiente de elevación de sección (\(F_{L} / \bar{q} S\)) versus ángulo de ataque (rad ^-1), que suponemos aquí que es constante para pequeños ángulos de ataque.

\(C_{M A C}\)es el coeficiente adimensional del momento de cabeceo aproximadamente\(AC\), normalmente positivo para un perfil aerodinámico acodado positivamente, pero cero para un perfil aerodinámico delgado no curvado.

Los experimentos en túnel de viento y la teoría aerodinámica muestran que las ecuaciones de acción aerodinámica\(\ref{eqn:11.15}\) son válidas solo para flujo constante, para lo cual el ángulo de ataque\(\alpha\) no varía con el tiempo. Sin embargo, aproximaremos un poco aquí y asumiremos que las ecuaciones\(\ref{eqn:11.15}\) son al menos cualitativamente válidas para el ángulo de ataque que varía lentamente en el tiempo,\(\alpha(t)=\alpha_{r}+\theta(t)\). Esta aproximación a veces se denomina aerodinámica cuasiestática o casi estable. Sustituir ecuaciones\(\ref{eqn:11.15}\) en ecuaciones\(\ref{eqn:11.14}\) da

\[J_{E A} \ddot{\theta}+k_{\theta} \theta=\bar{q} S C_{L \alpha}\left(\alpha_{r}+\theta\right) e+\bar{q} S c C_{M A C} \nonumber \]

\[\Rightarrow \quad J_{E A} \ddot{\theta}+\left(k_{\theta}-\bar{q} S C_{L \alpha} e\right) \theta=\bar{q} S C_{L \alpha} \alpha_{r} e+\bar{q} S c C_{M A C}\label{eqn:11.16} \]

\(\ref{eqn:11.16}\)Obsérvese en la Ecuación que la constante de rigidez total\(k_{\theta}-\bar{q} S C_{L \alpha} e\) (rigidez estructural más “rigidez” aerodinámica) puede, para\(e > 0\), llegar a ser cero o incluso negativa si la presión dinámica\(\bar{q}\) es suficientemente grande. Esto es críticamente importante en relación con la estabilidad del sistema. Consideremos flujo constante, por ejemplo, para lo cual\(\ddot{\theta}=0\); en este caso podemos resolver Ecuación\(\ref{eqn:11.16}\) algebraicamente para la rotación estructural estática:

\[\theta=\frac{\bar{q} S\left(C_{L \alpha} \alpha_{r} e+c C_{M A C}\right)}{k_{\theta}-\bar{q} S C_{L \alpha} e} \equiv \frac{\bar{q}\left(C_{L \alpha} \alpha_{r} e+c C_{M A C}\right)}{C_{L \alpha} e\left(\bar{q}_{D}-\bar{q}\right)}\label{eqn:11.17} \]

En Ecuación\(\ref{eqn:11.17}\), definimos la presión dinámica de divergencia en términos de otros parámetros fijos del sistema como

\[\bar{q}_{D} \equiv \frac{k_{\theta}}{S C_{L \alpha} e}\label{eqn:11.18} \]

Si es posible que un conjunto dado de parámetros físicos aumente la velocidad del aire del túnel de viento\(V\) hasta el punto de que\(\bar{q} \rightarrow \bar{q}_{D}=k_{\theta} / S C_{L \alpha} e\), entonces, a partir de la Ecuación\(\ref{eqn:11.17}\), claramente sucederá algo muy interesante. A partir de tus conocimientos de aerodinámica y estructuras, ¿qué tipos de comportamiento físico crees que son posibles? Tenga en cuenta que la ecuación\(\ref{eqn:11.17}\) se basa en los supuestos de ángulos pequeños y linealidad completa tanto de la aerodinámica como de las estructuras (en este sistema, el resorte de rotación).

Una superficie de control de avión convencional se monta en el borde de salida de una superficie de elevación principal, con el borde de ataque de la superficie de control articulado a la superficie de elevación (por ejemplo, un alerón en un ala). En este caso, el centro aerodinámico de la superficie de control se encuentra a popa del eje elástico, haciendo que el brazo de momento sea\(e\) negativo (ver Figura\(\PageIndex{3}\)). A partir de la ecuación\(\ref{eqn:11.17}\), esto produce el momento negativo\(\bar{q} S C_{L \alpha} \alpha_{r} e\), que se llama momento de soplado, y también aumenta la rigidez estructural en la constante de rigidez total\(k_{\theta}-\bar{q} S C_{L \alpha} e\). Por lo tanto, una superficie de control de borde de salida convencional no puede divergir aeroelásticamente.

Ejemplo\(\PageIndex{3}\): 2-DOF typical-section model for coupled wing being and torsion

Ahora volvemos a las Ecuaciones de movimiento plano-general 11.1.2, 11.1.3 y 11.1.4, que son tres ODE en tres DOF desconocidas:\(x_{C}(t)\),\(y_{C}(t)\), y\(\theta(t)\). En la práctica, estas ODE suelen estar acopladas por la geometría del sistema y la naturaleza de las acciones activas y reactivas. Además, si se permite que el movimiento tenga una magnitud arbitrariamente grande, entonces las ecuaciones suelen ser no lineales. En general, estas ecuaciones arbitrario-plano-movimiento pueden resolverse solo en forma numérica, no en forma de ecuaciones algebraicas. Sin embargo, los sistemas mecánicos considerados en este libro están limitados, en la mayoría de los casos, a aquellos para los que la traslación del centro de masa es pequeña en relación con las dimensiones del cuerpo rígido, y para los que la rotación es pequeña,\(|\theta(t)|<\approx 10^{\circ}\) (por ejemplo, los Ejemplos 11.3.1 y 11.3.2 en esta sección); estas limitaciones nos permiten linealizar las ODE en formas más fáciles de resolver.

Una de las primeras formas de aleteo aeroelástico del ala que se observó y analizó cuidadosamente a principios del siglo XX implica la flexión acoplada y la vibración torsional (Bisplinghoff et al. , 1955, Sección 9.2). La sección típica de dos grados de libertad (2-DOF) representada en la Figura\(\PageIndex{5}\) es un modelo estructural muy simplificado que se utiliza para estudiar el aleteo de flexión-torsión del ala ². La sección aerodinámica está articulada sin fricción en el eje elástico\(EA\) a una barra vertical (asumida rígida y de fuerza inercial insignificante), la cual está restringida a la traslación vertical por cojinetes lineales sin fricción. El resorte rotacional\(k_{\theta}\) simula la rigidez torsional del ala y el resorte traslacional\(k_{y}\) simula la rigidez de flexión del ala. La teoría de la aerodinámica inestable, incluso para el flujo bidimensional, es muy complicada, por lo que simplemente representaremos las acciones aerodinámicas resultantes generalmente como momento de elevación\(F_{L}(t)\) y cabeceo alrededor del centro aerodinámico\(M_{A C}(t)\), y nos centraremos en la dinámica estructural.

Figura\(\PageIndex{5}\): Ejemplo 11.3.3: Sección típica de 2-DOF

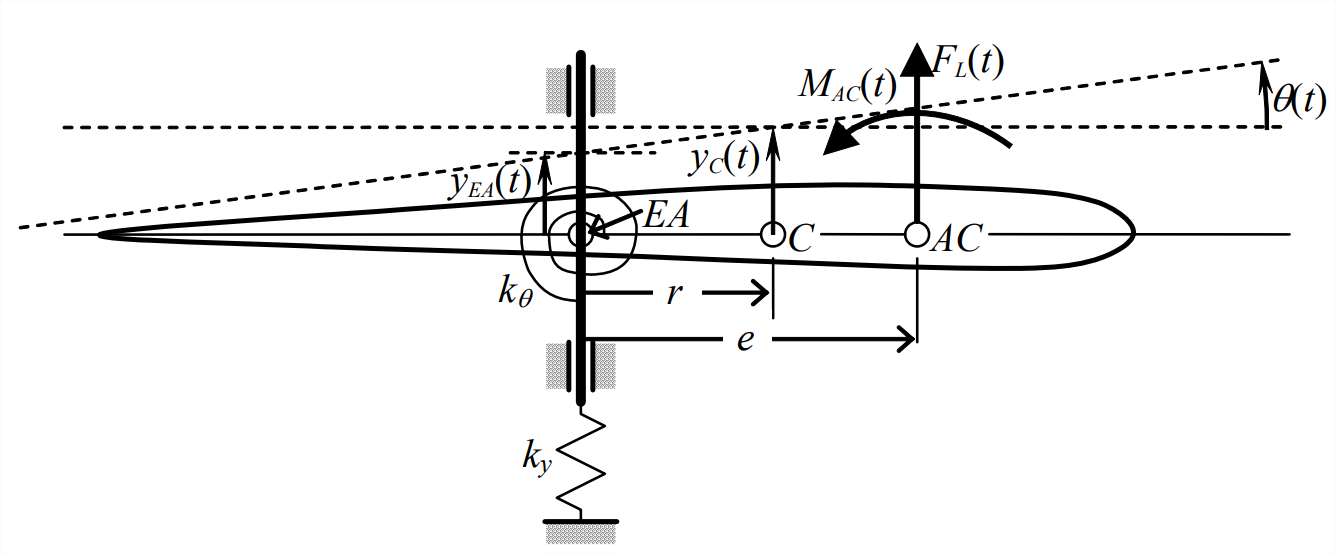
Para escribir las ecuaciones de movimiento para esta sección típica, seleccionamos como grados de libertad la traslación vertical del centro\(y_C(t)\) de masa\(C\), y la rotación de cabeceo\(\theta(t)\), ambas relativas a la posición de equilibrio estático de referencia. La geometría de la rotación pequeña está representada por la relación entre\(y_{\mathrm{C}}(t)\) y\(y_{E A}(t)\):

\[y_{C}(t)=y_{E A}(t)+r \sin \theta(t) \approx y_{E A}(t)+r \theta(t) \Rightarrow y_{E A}(t) \approx y_{C}(t)-r \theta(t)\label{eqn:11.19} \]

El DFBD asociado a la Figura\(\PageIndex{5}\) se dibuja a continuación, con Ecuación de aproximación\(\ref{eqn:11.19}\) utilizada para anotar la fuerza debida al resorte de traslación\(k_{y}\).

Figura\(\PageIndex{6}\)

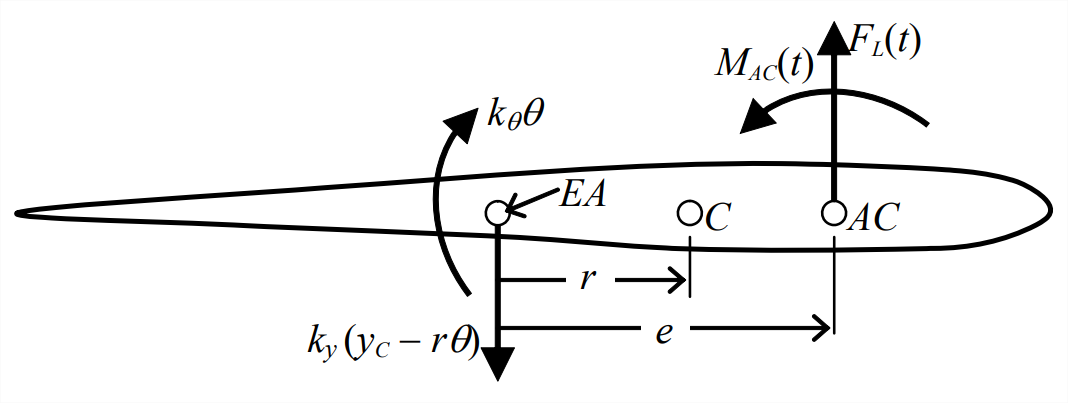
Usando este DFBD, escribimos las dos ecuaciones relevantes de movimiento, las Ecuaciones 11.1.3 y 11.1.4 en forma escalar, como

\[m \ddot{y}_{C}=F_{L}(t)-k_{y}\left(y_{C}-r \theta\right)\label{eqn:11.20a} \]

\[J_{C} \ddot{\theta}=(e-r) F_{L}(t)+M_{A C}(t)-k_{\theta} \theta+r k_{y}\left(y_{C}-r \theta\right)\label{eqn:11.20b} \]

Es apropiado expresar Ecuaciones\(\ref{eqn:11.20a}\)\(\ref{eqn:11.20b}\) con todos los términos que involucren grados de libertad\(y_{C}(t)\) y\(\theta(t)\) transpuestos a los lados izquierdos:

\[m \ddot{y}_{C}+k_{y} y_{C}-r k_{y} \theta=F_{L}(t)\label{eqn:11.21a} \]

\[J_{C} \ddot{\theta}-r k_{y} y_{C}+\left(k_{\theta}+r^{2} k_{y}\right) \theta=(e-r) F_{L}(t)+M_{A C}(t)\label{eqn:11.21b} \]

Las ecuaciones\(\ref{eqn:11.21a}\) y\(\ref{eqn:11.21b}\) son un par de 2 ^nd orden, ODE acopladas en incógnitas\(y_{C}(t)\) y\(\theta(t)\). Así como Ecuaciones\(\ref{eqn:11.15}\), Ecuaciones\(\ref{eqn:11.21a}\) y se\(\ref{eqn:11.21b}\) describen como acopladas porque cada ecuación contiene ambas variables dependientes y ninguna ecuación puede resolverse independientemente de la otra. Es posible, aunque no nos molestemos en hacerlo, combinar estas dos ecuaciones en una sola ODE de ^4º orden en una sola función desconocida del tiempo; por lo tanto, esta sección típica de 2-DOF es en realidad un sistema de 4to orden. Es apropiado y común también expresar el conjunto de Ecuaciones ODEs\(\ref{eqn:11.21a}\) y\(\ref{eqn:11.21b}\) en forma de matriz:

\ [\ overbrackets {\ left [\ begin {array} {cc}
m & 0\\
0 & J_ {C}
\ end {array}\ right]} ^ {\ text {matriz de inercia}}\ left [\ begin {array} {c}
\ ddot {y} _ {C}\\ ddot {
\ ddot {\ theta}
\ end {array}\ derecha] +\ overbrackets {izquierda\ [\ comenzar { array} {cc}
k_ {y} & -r k_ {y}\\
-r k_ {y} & k_ {\ theta} +r^ {2} k_ {y}
\ end {array}\ derecha]} ^ {\ text {matriz de rigidez estructural}}\ left [\ begin {array} {c}
y_ {C}
\\ theta
\ end {array}\ right =\ left [\ begin {array} {c}
F_ {L} (t)\\
(e-r) F_ {L} (t) +M_ {A C} (t)
\ final {matriz}\ derecha]\ etiqueta {eqn:11.22}\]

Las matrices de coeficientes del lado izquierdo etiquetadas de Ecuación\(\ref{eqn:11.22}\) son típicas de los sistemas dinámicos estructurales y exhiben algunas propiedades generales importantes. La matriz de inercia en este caso es diagonal; más generalmente, será no diagonal sino simétrica. La matriz de inercia siempre será positiva definida porque toda la materia tiene masa positiva; por lo tanto, el determinante de la matriz de inercia siempre será positivo. En Ecuación\(\ref{eqn:11.22}\), ese determinante es simplemente el producto\(m J_{C}>0\). La matriz de rigidez estructural en Ecuación\(\ref{eqn:11.22}\) es simétrica, y esta es una propiedad general resultante de la linealidad entre acciones aplicadas y deformaciones estructurales. Además, si una estructura está restringida por soportes conectados a tierra, como el resorte de rotación\(k_{\theta}\) y el resorte de traslación\(k_{y}\) de la sección típica, entonces cada uno de los elementos diagonales de la matriz de rigidez será positivo, y la matriz de rigidez en sí misma será positiva definida. Se puede comprobar fácilmente que el determinante de la matriz de rigidez en Ecuación\(\ref{eqn:11.22}\) es el producto\(k_{y} k_{\theta}>0\). El acoplamiento entre la traslación vertical\(y_{C}(t)\) y la rotación\(\theta(t)\) de cabeceo de la sección típica es producido y mostrado por los términos fuera de diagonal distintos de cero de la matriz de rigidez, siendo cada uno\(-r k_{y}\).

¹ Para la historia temprana de divergencia aeroelástica, ver Bisplinghoff et al. , 1955, págs. 3-7, y Gordon, 1978, págs. 259-270.

² Los perfiles aerodinámicos físicos de sección típica fueron diseñados, fabricados y probados en estudios recientes de investigación experimental de túnel de viento de aerodinámica inestable (como lo resume Bennett, 2000), y de control de retroalimentación para suprimir el aleteo (DeMarqui, et al. , 2005 y 2006). Tarea Problema 16.11 aplica una teoría aproximada de la aerodinámica inestable en una simulación de uno de esos proyectos experimentales.