14.3: Control de Circuito Cerrado de la Posición del Rotor (1)

Modifiquemos el sistema de control de bucle abierto de la Figura 14.2.1 de la siguiente manera: mida la salida con un sensor de posición de rotación, y envíe la salida de voltaje de este sensor de vuelta a una unión sumadora que forma la señal de error, que es la diferencia entre la señal que representa la configuración del operador y la señal que representa la salida real. La rama de retroalimentación y la unión sumadora convierten el sistema de bucle abierto en el sistema de bucle cerrado representado en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Diagrama funcional del sistema de control de posición-retroalimentación. (Copyright; autor vía fuente)

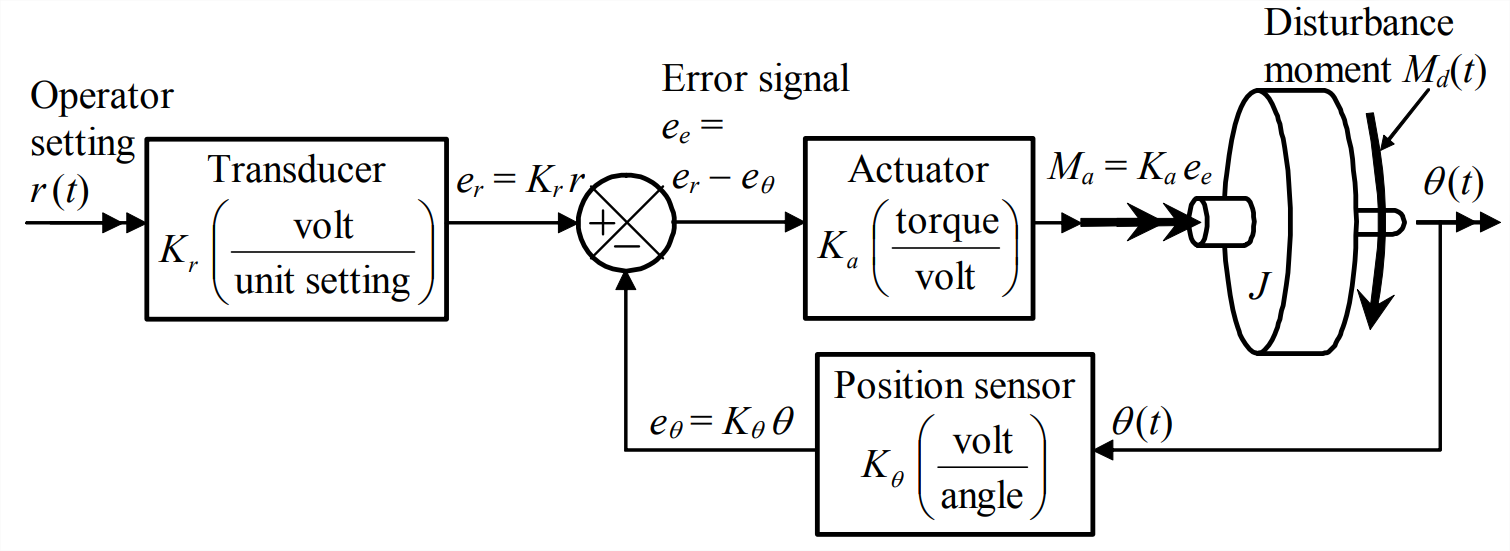
Los elementos del sistema de bucle cerrado son los mismos que los del sistema de bucle abierto, Figura 14.2.1, pero con la adición del sensor de salida y la unión sumadora (definida en la Sección 13.2). Suponemos que el sensor es un dispositivo como un codificador óptico, con sensibilidad positiva calibrada con precisión\(K_{\theta}\) (voltio por grado o radián). La unión sumadora podría ser un circuito simple consistente en un amplificador inversor (Figura 5.3.2) y un amplificador inversor sumador (tarea Problema 5.7).

Este sistema de bucle cerrado tiende a ser autocorregible. Podemos entender esta tendencia escribiendo en detalle la ecuación para el momento de control, a partir de las señales etiquetadas en la Figura\(\PageIndex{1}\):

\[M_{a}(t)=K_{a} e_{e}(t)=K_{a}\left[e_{r}(t)-e_{\theta}(t)\right]=K_{a}\left[K_{r} r(t)-K_{\theta} \theta(t)\right]\label{eqn:14.11} \]

De Ecuación\(\ref{eqn:14.11}\), el momento de control es cero cuando\(K_{r} r(t)-K_{\theta} \theta(t)=0\), de modo que

\[\theta(t)=\frac{K_{r}}{K_{\theta}} r(t)\label{eqn:14.12} \]

Ecuación\(\ref{eqn:14.12}\) claramente es la relación lineal instantánea deseada de salida\(\theta(t)\) a entrada\(r(t)\). En instantes cuando la Ecuación no\(\ref{eqn:14.12}\) está satisfecha, el actuador de control impone un momento correctivo. Supongamos, por ejemplo, que en cierto instante ambos\(\theta(t)\) y\(r(t)\) son positivos, pero que la salida es menor que el valor deseado,\(\theta(t)<\left[K_{r} / K_{\theta}\right] r(t)\); en este instante, entonces, la señal de error es\(K_{r} r(t)-K_{\theta} \theta(t)=e_{e}(t)>0\), y\(M_{a}(t)=K_{a} e_{e}(t)>0\) así, cuando la salida es menor de lo que debería ser, el sistema de control de bucle cerrado impone un momento positivo para incrementar la producción. Además, al revertir los signos de desigualdad anteriores, se puede demostrar que el sistema de control impone un momento negativo para disminuir la salida cuando la salida es mayor de lo que debería ser.

Debido a que el momento correctivo es proporcional al error de salida y es independiente del modelo teórico, la tendencia de autocorrección de este sistema de control de bucle cerrado está vigente independientemente de lo bien que el modelo teórico represente el sistema y su entorno.

Para inferir más información sobre el sistema de bucle cerrado de la Figura\(\PageIndex{1}\), derivemos la ODE del movimiento sustituyendo la Ecuación\(\ref{eqn:14.11}\) en la Ecuación 14.2.1:

\[J \ddot{\theta}=M_{a}(t)+M_{d}(t)=K_{a}\left[K_{r} r(t)-K_{\theta} \theta(t)\right]+M_{d}(t) \nonumber \]

\[\Rightarrow \quad J \ddot{\theta}+K_{a} K_{\theta} \theta=K_{a} K_{r} r(t)+M_{d}(t)\label{eqn:14.13} \]

A partir de la Ecuación\(\ref{eqn:14.13}\), hacemos las siguientes observaciones:

1. el control de retroalimentación en la Figura\(\PageIndex{1}\) tiene el efecto de unir entre la configuración del operador y la inercia del rotor un resorte de restauración artificial con constante de rigidez\(K_{a} K_{\theta}\);
2. si solo\(r(t)\) actúa la entrada del operador, es decir\(M_{d}(t)=0\), si, entonces la ecuación de salida deseada\(\ref{eqn:14.12}\) es realmente la respuesta pseudo-estática del sistema (como se define en la Sección 7.1), \[K_{a} K_{\theta} \theta_{p s}=K_{a} K_{r} r(t) \Rightarrow \theta_{p s}(t)=\frac{K_{r}}{K_{\theta}} r(t)\label{eqn:14.14} \]
3. si solo\(r(t)\) actúa la entrada del operador, y si la sensibilidad del transductor de entrada es igual a la sensibilidad del sensor de salida\(K_{r}=K_{\theta}\), entonces el sistema de bucle cerrado es directamente análogo a un sistema de resorte de masa excitado por la base sin amortiguar [como se describe en la Ecuación 13.2.1 con\(c = 0\)];
4. la tendencia autocorrectora incluso contrarresta la influencia adversa de muchos tipos de perturbaciones, lo que podemos concluir de nuestra experiencia previa con soluciones de respuesta forzada para sistemas ^{de segundo} orden.

Si, por ejemplo, la perturbación está limitada en el tiempo, tal como un pulso, entonces la respuesta posterior al pulso oscilará alrededor de cero pero no contendrá ningún componente constante de estado estacionario. Si, por otro ejemplo, la perturbación es sinusoidal, entonces la respuesta resultante oscilará alrededor de cero pero no contendrá ningún componente constante de estado estacionario; sin embargo, también podemos ver que si la frecuencia de la perturbación sinusoidal está en la vecindad de la frecuencia natural del sistema de bucle cerrado, \(\omega_{n}=\sqrt{K_{a} K_{\theta} / J}\), entonces la perturbación podría producir resonancia, que este sistema de control en particular no pudo evitar.

Para establecer el método de análisis posterior de sistemas de control más complicados, dibujemos y analicemos el diagrama de bloques de Laplace correspondiente al diagrama funcional Figura\(\PageIndex{1}\). Para esta tarea, definimos las siguientes transformadas de Laplace:\(L[r(t)] \equiv R(s)\)\(L[\theta(t)] \equiv \Theta(s)\),\(L\left[e_{r}(t)\right] \equiv E_{r}(s)\),\(L\left[e_{\theta}(t)\right] \equiv E_{\theta}(s)\),\(L\left[e_{e}(t)\right] \equiv E_{e}(s)\),\(L\left[M_{a}(t)\right] \equiv \mathrm{M}_{\mathrm{a}}(s)\),\(L\left[M_{d}(t)\right] \equiv \mathrm{M}_{\mathrm{d}}(s)\), y\(L[M(t)] \equiv \mathrm{M}(s)\). El diagrama de bloques de Laplace, Figura\(\PageIndex{2}\), es similar al diagrama funcional, excepto que reemplazamos el rotor en la Figura\(\PageIndex{1}\) con su función de transferencia,\(P T F(s)\) de la Ecuación 14.1.2, y usamos una unión sumadora para denotar las acciones sobre el rotor tanto del momento\(M_{a}(t)\) de control como de momento de perturbación\(M_{d}(t)\).

Figura\(\PageIndex{2}\): Diagrama de bloques de Laplace, incluyendo entrada de perturbaciones, del sistema de control de posición-retroalimentación. (Copyright; autor vía fuente)

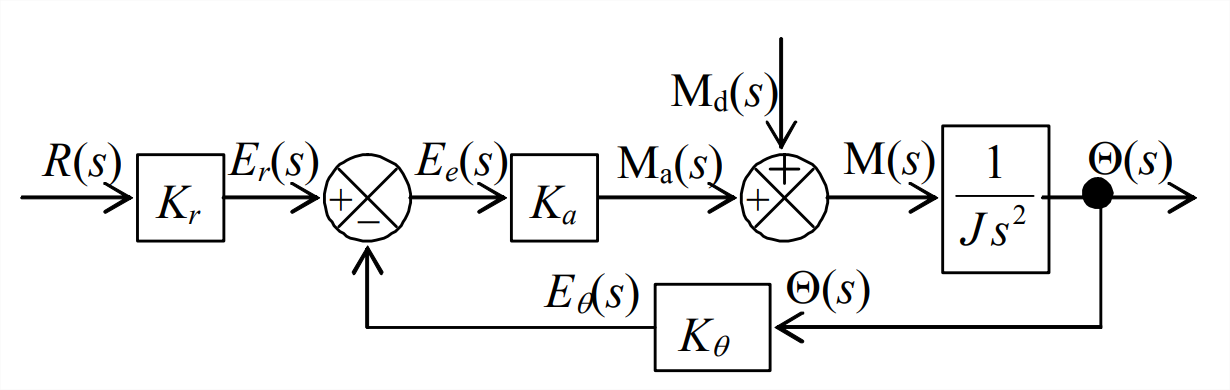
Este sistema en realidad tiene dos entradas independientes,\(r(t)\) y\(M_d(t)\), por lo tanto, no es estrictamente un sistema de entrada única salida (SISO). Sin embargo, la relación fundamental más importante para este sistema de control es la que existe entre la entrada y la salida de referencia\(\theta(t)\), por lo que ahora nos enfocaremos en esa relación estableciendo\(M_{d}(t)=0\). Por lo tanto\(\mathrm{M}_{\mathrm{d}}(s)=0\),, y volvemos a dibujar Figura\(\PageIndex{2}\) como el diagrama de bloques SISO a la derecha, con el objetivo de derivar de ella la función de transferencia de bucle cerrado,\(\operatorname{CLTF}(s) \equiv \Theta(s) / R(s)\).

Figura\(\PageIndex{3}\): Diagrama de bloques de Laplace del sistema de control de posición-retroalimentación SISO. (Copyright; autor vía fuente)

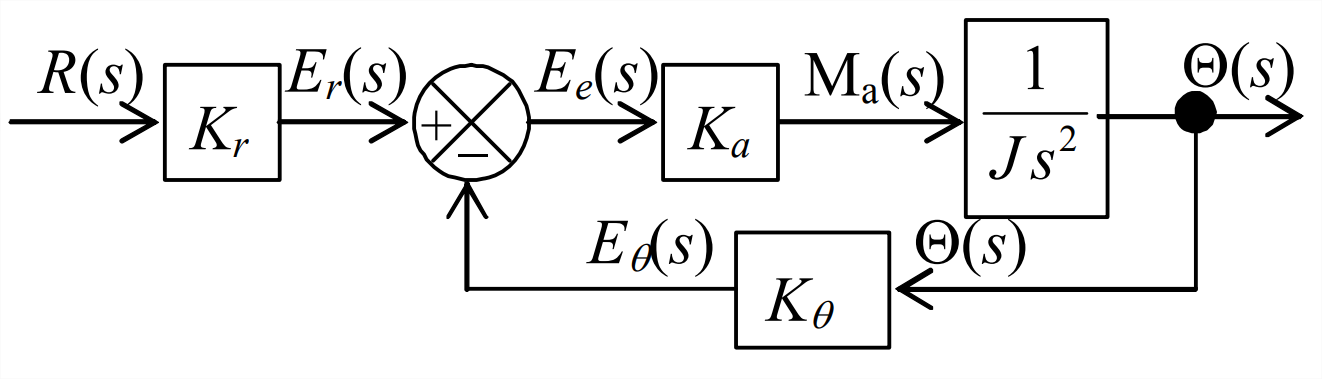
Se requieren tres pasos distintos de álgebra de diagrama de bloques para reducir la figura\(\PageIndex{3}\) a un solo bloque, el\(\operatorname{CLTF}(s)\), que separa las señales de entrada y salida:

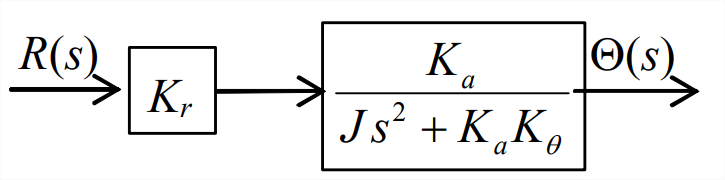
1. Combine (multiplique) las dos funciones de transferencia de bloques dentro de la rama directa del bucle, como se muestra a continuación. Esta operación de multiplicación se deriva en la Sección 13.1.

   

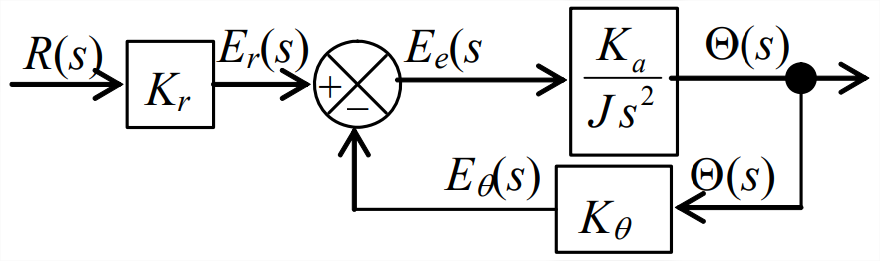
   Figura\(\PageIndex{4}\): Paso 1. (Copyright; autor vía fuente)

2. Resuelva las funciones de transferencia de rama directa y derivación de retroalimentación del bucle cerrado en la función de transferencia equivalente única que se muestra a continuación. El álgebra de diagrama de bloques utilizado en este paso se deriva en la siguiente sección; es una herramienta básica importante para el análisis de sistemas de control.

   

   Figura\(\PageIndex{5}\): Paso 2. (Copyright; autor vía fuente)

3. Por último, y obviamente, simplemente multiplique los dos bloques restantes para producir el resultado requerido que se muestra a continuación.

   

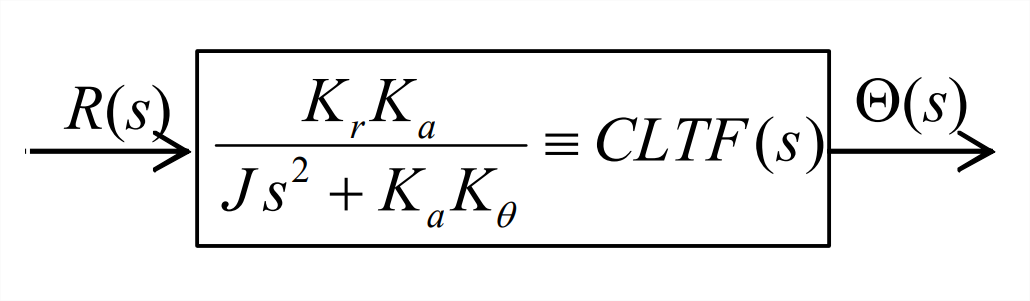
   Figura\(\PageIndex{6}\): Paso 3. (Copyright; autor vía fuente)

Para este sistema relativamente simple, la versión SISO de ODE de Ecuación de movimiento\(\ref{eqn:14.13}\) es\(J \ddot{\theta}+K_{a} K_{\theta} \theta=K_{a} K_{r} r(t)\). Es muy fácil derivar lo mismo\(\operatorname{CLTF}(s)\) directamente de esta ODE, pero hemos derivado\(\operatorname{CLTF}(s)\) aquí usando álgebra de diagrama de bloques para establecer el enfoque que es apropiado para sistemas más complicados.

Revisitaremos este sistema de control de posición-retroalimentación en la Sección 14.5, con los objetivos de evaluar su desempeño de control y luego desarrollar una adición a los sistemas que mejoren el desempeño.