14.4: Función de transferencia de un solo lazo cerrado

Considere Figura\(\PageIndex{1}\), que es una versión más general, en notación estándar, del bucle cerrado en la Figura 14.3.4. Funciones generales\(G(s)\) y\(H(s)\) son, respectivamente, las funciones de transferencia de rama directa y rama de retroalimentación. \(E(s)\)es la señal de error de accionamiento y\(B(s)\) es la señal de retroalimentación. Buscamos la función de transferencia de bucle cerrado, la relación\(\operatorname{Out}(s) / \operatorname{In}(s)\).

Figura\(\PageIndex{1}\): Diagrama de bloques de Laplace de bucle cerrado general. (Copyright; autor vía fuente)

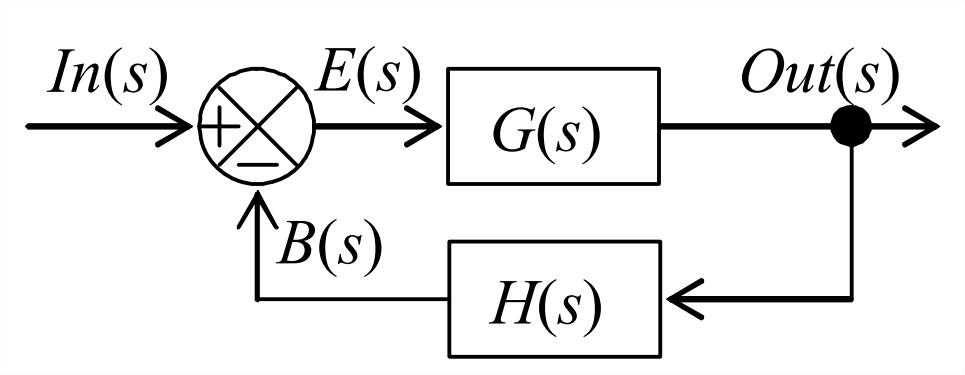
Todas las cantidades etiquetadas en la Figura\(\PageIndex{1}\) se denotan como funciones de la variable Laplace\(s\), pero es importante reconocer que existen dos tipos de funciones fundamentalmente diferentes:

1. las “señales”\(\operatorname{In}(s)\),,\(E(s)\), y\(B(s)\)\(\operatorname{Out}(s)\), que en realidad son transformadas de Laplace de variables dependientes del tiempo como el movimiento y la tensión; y
2. las funciones de transferencia\(G(s)\) y\(H(s)\), que representan en el dominio de Laplace las características de sistemas y objetos como la inercia y los circuitos. Para enfatizar la diferencia en la siguiente derivación de\(\operatorname{Out}(s) / \operatorname{In}(s)\), omita la notación funcional “(\(s\))” de las señales, al menos en los pasos intermedios. Los pasos siguen naturalmente de la Figura\(\PageIndex{1}\):

\[E=I n-B \quad \text { and } \quad B=O u t \times H(s), \nonumber \]

\[\Rightarrow \quad O u t=E \times G(s)=[\operatorname{In}-B] \times G(s)=[\operatorname{In}-O u t \times H(s)] \times G(s) \nonumber \]

\[=\operatorname{In} \times G(s)-O u t \times H(s) \times G(s) \nonumber \]

\[\Rightarrow \quad O u t \times[1+G(s) H(s)]=\operatorname{In} \times G(s) \nonumber \]

\[\Rightarrow \frac{O u t(s)}{\operatorname{In}(s)}=\frac{G(s)}{1+G(s) H(s)}\label{eqn:14.15} \]

\(\ref{eqn:14.15}\)La ecuación es una herramienta importante, general y ahorradora de mano de obra para el análisis de bucles en cualquier sistema de control, no solo los sistemas discutidos en este capítulo. Para ilustrar su aplicación, utilicémosla para derivar en detalle la función de transferencia de bucle escrita en el Paso 2 del álgebra de diagrama de bloques de la Sección 14.3. A partir del Paso 1 de ese proceso (o de la Figura 14.3.4), identificamos:\(G(s)=K_{a} / J s^{2}\) y\(H(s)=K_{\theta}\). Sustituyendo estos en Ecuación\(\ref{eqn:14.15}\) da\(\frac{\operatorname{Out}(s)}{\operatorname{In}(s)}=\frac{K_{a} / J s^{2}}{1+\left(K_{a} / J s^{2}\right) K_{\theta}}=\frac{K_{a}}{J s^{2}+K_{a} K_{\theta}}\), que es la función de transferencia de bucle que se muestra en el diagrama de bloques como resultado del Paso 2.

Una función de transferencia en Ecuación\(\ref{eqn:14.15}\) a menudo tiene la forma de una relación de polinomios en\(s\), como\(G(s)\) en el párrafo anterior, por lo que es útil derivar una versión de Ecuación\(\ref{eqn:14.15}\) en términos de los polinomios. Primero, definimos polinomios numeradores y denominador que componen\(G(s)\) y\(H(s)\):

\[G(s) \equiv \frac{N_{G}(s)}{D_{G}(s)} \text { and } H(s) \equiv \frac{N_{H}(s)}{D_{H}(s)}\label{eqn:14.16} \]

A continuación, realizamos el álgebra de Ecuación\(\ref{eqn:14.15}\), dejando caer la notación funcional “(\(s\))” de las funciones de transferencia y polinomios en aras de la concisión notacional:

\[\frac{O u t(s)}{\operatorname{In}(s)}=\frac{G}{1+G H}=\frac{N_{G} / D_{G}}{1+\left(N_{G} / D_{G}\right) \times\left(N_{H} / D_{H}\right)}=\frac{N_{G} D_{H}}{D_{G} D_{H}+N_{G} N_{H}}\label{eqn:14.17} \]

Para el ejemplo del párrafo anterior, los polinomios simples son\(N_{G}=K_{a}\),,\(D_{G}=J_{S}^{2}\)\(N_{H}=K_{\theta}\), y\(D_{H}=1\); sustituyendo estos términos en Ecuación\(\ref{eqn:14.17}\) obviamente conduce al,\(\operatorname{Out}(s) / \operatorname{In}(s)\) resultado derivado en el párrafo anterior, pero con un poco menos álgebra porque el álgebra ha sido completado en Ecuación\(\ref{eqn:14.17}\). La ecuación\(\ref{eqn:14.17}\) expresa la función de transferencia de bucle cerrado como una relación de polinomios, y se aplica en general, no solo a los problemas de este capítulo.

Por último, utilizaremos posteriormente una forma aún más especializada de Ecuaciones\(\ref{eqn:14.15}\) y\(\ref{eqn:14.17}\) para el caso de la retroalimentación de unidad,\(H(s)=1=1 / 1\):

\[\frac{\operatorname{Out}(s)}{\operatorname{In}(s)}=\frac{G}{1+G}=\frac{N_{G}}{D_{G}+N_{G}}\label{eqn:14.18} \]

Ecuaciones\(\ref{eqn:14.15}\)\(\ref{eqn:14.17}\),, y\(\ref{eqn:14.18}\) son muy útiles para el análisis del control de retroalimentación. En el futuro, cada vez que encuentre un bucle simple con la forma de Figura\(\PageIndex{1}\) en el diagrama de bloques de Laplace de un sistema, puede (y generalmente debería) aplicar cualquiera de estas ecuaciones que sea más apropiada para derivar la función de transferencia de bucle, sin repetir el álgebra que entra en el derivación de estas ecuaciones.