16.5: Loci de raíces para sistemas de tercer orden

En la Sección 16.4, se utilizó la fórmula cuadrática para evaluar fácilmente los loci de raíces para sistemas ^{de segundo} orden. Sin embargo, es más típico en la práctica que los sistemas de ingeniería tengan órdenes superiores al ^segundo orden, por lo que determinar los loci de raíces requiere resolver repetidamente ecuaciones polinómicas de ^3º y grados superiores, lo que puede ser una tarea desafiante. Esta sección introduce con el ejemplo los métodos de solución para sistemas de orden superior que se utilizan comúnmente en la práctica.

^{Para este ejemplo, consideramos nuevamente el sistema descrito en la Sección 16.3 (Figuras 16.3.1, 16.3.2 y 16.3.3), un sistema de control de posición-retroalimentación del rotor con un filtro paso bajo de primer orden en la rama de retroalimentación.} Función de transferencia de bucle cerrado La ecuación 16.3.9 da la ecuación característica de ^tercer grado en dos formas algebraicas diferentes, una de las cuales es

\[\operatorname{Den}(p)=a_{1} p^{3}+a_{2} p^{2}+a_{3} p+a_{4}=p^{3}+\left(\frac{1}{\tau_{L}}+\frac{c_{\theta}}{J}\right) p^{2}+\frac{c_{\theta}}{J} \frac{1}{\tau_{L}} p+\frac{K_{a} K_{\theta}}{J \tau_{L}}=0\label{eqn:16.51a} \]

^{En la Sección 16.3, mantenemos constante la inercia del rotor\(J\), la constante\(c_{\theta}\) de amortiguación viscosa de los cojinetes y la constante\(\tau_{L}\) de tiempo del filtro paso bajo de primer orden, todos los valores positivos; en particular, elegimos para la evaluación numérica los valores\(c_{\theta} / J=100\) s -1, y, para} la frecuencia de rotura del filtro,\(\omega_{b} \equiv 1 / \tau_{L}=300\) rad/s. Permitimos que el valor del producto\(K_{a} K_{\theta}\) de las sensibilidades del sistema de control variara. Usando los criterios de Routh, determinamos los límites de estabilidad inferior y superior para el parámetro\(K_{a} K_{\theta} / J \equiv \Lambda\): el sistema es positivamente estable siempre que\(0<\Lambda<40,000\) s ^-2.

Ahora, hagamos una evaluación más detallada de la estabilidad calculando y trazando los loci de raíces como\(\Lambda\) varía, utilizando los mismos valores numéricos de las otras constantes que en la Sección 16.3. Resolvemos numéricamente para las raíces de la ecuación polinómica\(\ref{eqn:16.51a}\) usando la operación raíz de MATLAB: para cada valor de\(\Lambda\), la entrada es la matriz de coeficientes\ (\ left [\ begin {array} {llll}
a_ {1} & a_ {2} & a_ {3} & a_ {4}
\ end {array}\ right]\), y el output es la\(3 \times 1\) matriz de raíces. Calcularemos y trazaremos los loci de raíces dos veces: primero, para un conjunto de\(\Lambda\) valores que elegimos (adivinar) de manera algo arbitraria para abarcar todo el rango posible de interés práctico; segundo, para otro conjunto de\(\Lambda\) valores que se refinan, con base en los resultados de la primera pasada, para enfocarnos en las raíces específicas de mayor significación práctica.

Para la primera pasada, variamos\(\Lambda\) de −30,000 s ^-2 a +70,000 s ^-2 en incrementos de 10,000 s ^-2. El siguiente es un archivo M de script MATLAB que calcula las raíces de la ecuación polinómica\(\ref{eqn:16.51a}\) repetidamente sobre estos valores de\(\Lambda\), luego imprime los valores de entrada y salida en una tabla, luego traza los loci de raíces:

%Matlabdemo163.m

% Estabilidad de un rotor amortiguado con retroalimentación de posición filtrada de paso bajo

%Loci de raíces

wb=300; CoVRJ=100; a2=Wb+COvrJ; A3=WB*COvrJ;

Lm= [-3 -2 -1 0 1 2 3 4 5 6 7] *1.0e4; Np = longitud (Lm);

para I=1:NP;

A4=LM (i) *wb;

p (i, 1:3) =raíces ([1 a2 a3 a4]). ' ;

final

NC=1:NP; anout= [nc' Lm' p];

disp ('Raíces #, Lambda, p'), disp (anout)

plot (p, 'kx'), grid, xlabel ('Parte real del polo (seg^-^1) ')

ylabel ('Imag parte del polo (seg^-^1) ')

title ('Loci de raíces de un sistema de órdenes 3^r^d como varias\ Lambda')

El comando para ejecutar el archivo M, y la salida tabular resultante sigue:

>> MatlabDemo163

Raíces #, Lambda, p

1.0e+004 *

0.0001 -3.0000 -0.0253 + 0.0141i -0.0253 - 0.0141i 0.0107

0.0002 -2.0000 -0.0242 + 0.0111i -0.0242 - 0.0111i 0.0085

0.0003 -1.0000 -0.0227 + 0.0056i -0.0227 - 0.0056i 0.0055

0.0004 0 0 -0.0300 -0.0100

0.0005 1.0000 -0.0337 -0.0031 + 0.0089i -0.0031 - 0.0089i

0.0006 2.0000 -0.0363 -0.0019 + 0.0127i -0.0019 - 0.0127i

0.0007 3.0000 -0.0383 -0.0008 + 0.0153i -0.0008 - 0.0153i

0.0008 4.0000 -0.0400 -0.0000 + 0.0173i -0.0000 - 0.0173i

0.0009 5.0000 -0.0415 0.0007 + 0.0190i 0.0007 - 0.0190i

0.0010 6.0000 -0.0428 0.0014 + 0.0205i 0.0014 - 0.0205i

0.0011 7.0000 -0.0440 0.0020 + 0.0217i 0.0020 - 0.0217i

La gráfica loci-de-raíces asociada (después del uso de las características de edición de MATLAB para anotación y mejora gráfica) es Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Loci de primer paso de raíces de Ecuación\(\ref{eqn:16.51a}\) para parámetros de control variables\(\Lambda=K_{a} K_{\theta} / J\). (Copyright; autor vía fuente)

Deducimos de\(\PageIndex{1}\) la Figura la siguiente información relevante. Porque\(\Lambda<0\), el sistema tiene un polo inestable asociado con una respuesta monótona de tiempo exponencialmente creciente; ya sabíamos por Routh que el sistema es inestable para\(\Lambda<0\), pero Routh no reveló el tipo de respuesta. Porque\(\Lambda=0\), los polos son todos reales y tienen los valores 0, −100 y −300 s ^-1. Esto también es obvio en la forma algebraica alternativa de la ecuación característica ^{de tercer} grado que proviene de la función de transferencia de bucle cerrado Ecuación 16.3.9:

\[\operatorname{Den}(p)=p\left(p+c_{\theta} / J\right)\left(p+\omega_{b}\right)+\omega_{b} \Lambda=0\label{eqn:16.51b} \]

De la Ecuación\(\ref{eqn:16.51a}\) con\(\Lambda=0\), los polos son claramente\(p_1 = 0\),\(p_{2}=-c_{\theta} / J=-100\) s ^-1, y\(p_3 = -\omega_{b} \equiv-1 / \tau_{L}=-300\) s ^-1. Las flechas de la Figura\(\PageIndex{1}\) indican las direcciones de los loci a medida que\(\Lambda\) aumenta. Las flechas muestran que hay un punto de ruptura (como se define en la Figura 16.4.1) para\(\Lambda\) algún lugar en el rango\(-10,000 s ^{-2}<\Lambda<0\), y un punto de ruptura para\(\Lambda\) algún lugar en el rango\(0<\Lambda<+10,000\) s ^-2. Para referencia futura, denotemos el valor de ruptura de\(\Lambda\) as\(\Lambda_{b a}\), que aún no está determinado. También observamos a partir de la Figura\(\PageIndex{1}\) y las raíces tabuladas que el límite superior de estabilidad (con raíces puramente complejas,\(p_{2,3}=\pm j 173\) rad/s) es\(\Lambda=40,000\) s ^-2, y que la respuesta temporal es oscilatoria para valores de\(\Lambda\) en las proximidades del límite superior; sabíamos de Routh el valor del límite superior, pero no el tipo de respuesta. Además, dado que el polo real para\(\Lambda>\Lambda_{b a}\) está asociado con una decadencia exponencial fuertemente amortiguada, los loci complejos para\(\Lambda>\Lambda_{b a}\) de la Figura\(\PageIndex{1}\) sugieren que la respuesta de tiempo es principalmente oscilatoria para\(\Lambda>\Lambda_{b a}\). Consulte la Figura 16.3.3 para ver ejemplos de esta respuesta principalmente oscilatoria. Porque\(\Lambda>\Lambda_{b a}\), este sistema tiene un modo exponencial de respuesta fuertemente amortiguado y un modo oscilatorio ligeramente amortiguado, y este último, con polos más cercanos al eje imaginario, es el modo dominante.

Ahora vamos a refinar el cálculo de loci-de-raíces, utilizando un nuevo conjunto de\(\Lambda\) valores que serían de mayor interés práctico. Este conjunto probablemente consistiría en valores para los que el sistema es estable, es decir,\(0<\Lambda<40,000\) s ^-2. El valor\(\Lambda_{b a}\) es significativo: es el límite entre un sistema (con\(0<\Lambda<\Lambda_{b a}\)) para el cual toda la respuesta transitoria está decayendo exponencial y un sistema (con\(\Lambda_{b a}<\Lambda\)) para el cual la respuesta transitoria dominante es oscilatoria. Ciertamente podríamos elegir el conjunto refinado de valores λ por ensayo numérico y error, permitiendo que MATLAB haga la mayor parte del trabajo. No obstante, esta situación brinda la oportunidad de introducir un enfoque teórico y más sistemático, que consideraremos a continuación. Este enfoque es general, pero nuestro objetivo limitado en esta introducción será determinar teóricamente solo el límite superior de la estabilidad\(\Lambda \equiv \Lambda_{u b}\), y el valor de ruptura\(\Lambda_{b a}\).

Este enfoque se basa en la forma Ecuación\(\ref{eqn:16.51b}\) de la ecuación característica, que reescribimos como

\[p\left(p+c_{\theta} / J\right)\left(p+\omega_{b}\right)=-\omega_{b} \Lambda\label{eqn:16.52} \]

Es importante que los polos del subsistema estén separados en factores en el lado izquierdo de la Ecuación\(\ref{eqn:16.52}\). Cada factor es un número complejo, en general, y puede expresarse en forma polar compleja, como se describe en la Sección 2.1. Es útil considerar cada factor como un vector complejo bidimensional con su cola en el polo del subsistema, para que escribamos

\[p=p-0 \equiv r_{1} e^{j \theta_{1}}, p+c_{\theta} / J=p-\left(-c_{\theta} / J\right) \equiv r_{2} e^{j \theta_{2}}, p+\omega_{b}=p-\left(-\omega_{b}\right) \equiv r_{3} e^{j \theta_{3}}\label{eqn:16.53} \]

El lado derecho real de la ecuación\(\ref{eqn:16.52}\) también está escrito en forma polar:\(-\omega_{b} \Lambda= \omega_{b} \Lambda \exp [j(\pm \pi, \pm 3 \pi, \ldots)]\). Por lo tanto, toda la ecuación característica se expresa en la siguiente forma polar, que cualquier raíz debe satisfacer:

\[r_{1} e^{j \theta_{1}} \times r_{2} e^{j \theta_{2}} \times r_{3} e^{j \theta_{3}}=r_{1} r_{2} r_{3} e^{j\left(\theta_{1}+\theta_{2}+\theta_{3}\right)}=\omega_{b} \Lambda \exp [j(\pm \pi, \pm 3 \pi, \ldots)]\label{eqn:16.54} \]

Figura\(\PageIndex{2}\) (Copyright; autor vía fuente)

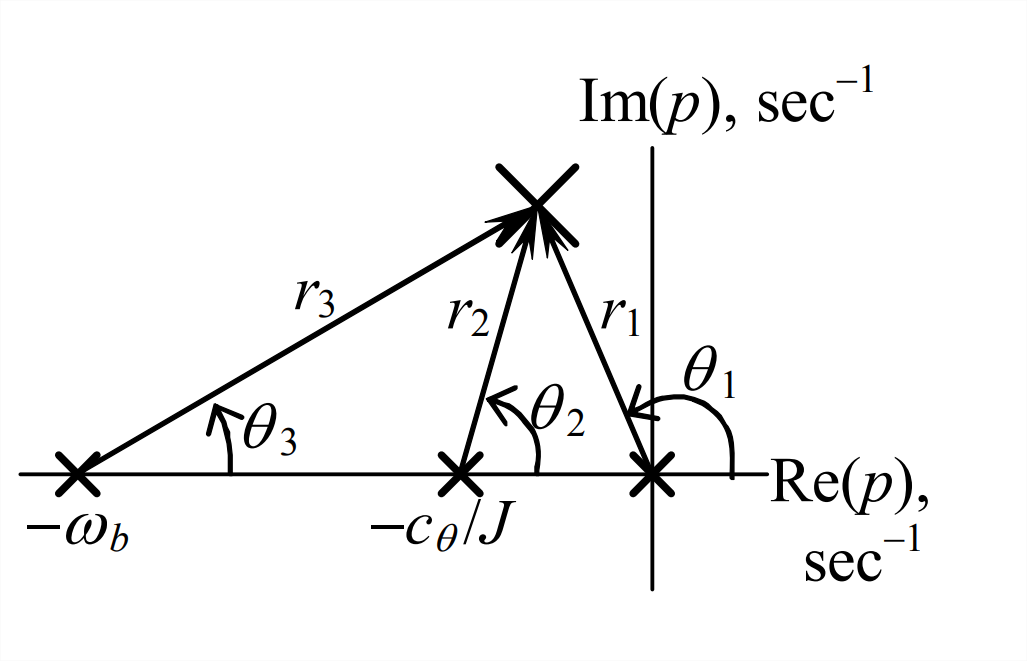
El dibujo anterior es una representación gráfica tanto de los vectores polares de la ecuación como de la ecuación\(\ref{eqn:16.53}\) característica de la ecuación\(\ref{eqn:16.54}\). Los pequeños\(\times\) son los polos del subsistema, en los que se ubican las colas de los vectores complejos. El grande\(\mathbf{X}\) es un polo del sistema completo, es decir, una raíz de la Ecuación\(\ref{eqn:16.51b}\), y un valor que satisface la Ecuación\(\ref{eqn:16.54}\). Ecuación compleja\(\ref{eqn:16.54}\) La ecuación incluye dos ecuaciones reales, las cuales deben ser satisfechas por cualquier polo del sistema. La primera ecuación es la igualdad de ángulos en los dos lados de la ecuación\(\ref{eqn:16.54}\):

\[\theta_{1}+\theta_{2}+\theta_{3}=\pm \pi, \pm 3 \pi, \ldots\label{eqn:16.55} \]

La segunda ecuación es la igualdad de magnitudes:

\[r_{1} r_{2} r_{3}=\omega_{b} \Lambda \Rightarrow \Lambda=\frac{r_{1} r_{2} r_{3}}{\omega_{b}}\label{eqn:16.56} \]

Para nuestra primera aplicación de este enfoque, usemos Ecuación\(\ref{eqn:16.55}\) para encontrar el polo\(j \omega_{d}\) en el límite superior de estabilidad\(\Lambda_{u b}\), y luego Ecuación\(\ref{eqn:16.56}\) para encontrar el valor de\(\Lambda_{u b}\) sí mismo. El poste se muestra en el dibujo a la derecha. Tenemos por definición para este límite de estabilidad:\(r_{1}=\omega_{d}\) y\(\theta_{1}=\pi / 2\). Por lo tanto, la Ecuación\(\ref{eqn:16.55}\) da\(\theta_{2}+\theta_{3}=\pi / 2\). [Descartamos las otras posibilidades\(-\pi, \pm 3 \pi, \ldots\) en Ecuación\(\ref{eqn:16.55}\) simplemente inspeccionando la figura.] Ahora se requiere algo de trigonometría. Ángulo\(\alpha\) entre las puntas de flecha de\(r_1\) y\(r_2\) está etiquetado en el dibujo. Los ángulos\(\alpha\) y\(\theta_{3}\) son los ángulos agudos complementarios de un triángulo rectángulo, así que también tenemos\(\alpha+\theta_{3}=\pi / 2\). Por lo tanto,\(\alpha=\theta_{2}\). De ahí que nos encontramos\(\omega_{d}\) igualando las tangentes de los dos triángulos rectos similares:

Figura\(\PageIndex{3}\) (Copyright; autor vía fuente)

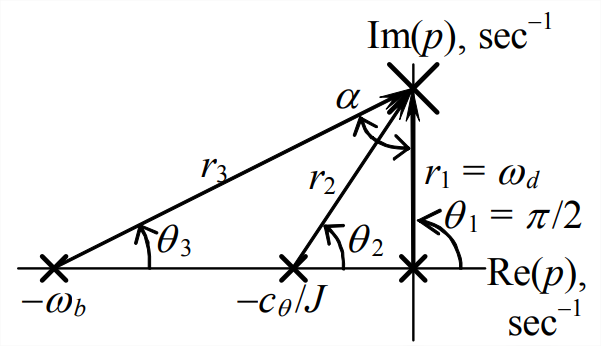
\[\tan \theta_{2}=\frac{\omega_{d}}{c_{\theta} / J}=\tan \alpha=\frac{\omega_{b}}{\omega_{d}} \Rightarrow \omega_{d}=\sqrt{\omega_{b} \frac{c_{\theta}}{J}}=\sqrt{300 \mathrm{s}^{-1} \times 100 \mathrm{s}^{-1}}=173.2 \frac{\mathrm{rad}}{\mathrm{s}} \nonumber \]

Teniendo\(\omega_{d}=r_{1}\), podemos utilizar el teorema de Pitágoras para encontrar\(r_{2}=\sqrt{\omega_{d}^{2}+\left(c_{\theta} / J\right)^{2}}=\sqrt{\omega_{b}\left(c_{\theta} / J\right)+\left(c_{\theta} / J\right)^{2}}\) y\(r_{3}=\sqrt{\omega_{d}^{2}+\omega_{b}^{2}}=\sqrt{\omega_{b}\left(c_{\theta} / J\right)+\omega_{b}^{2}}\). Finalmente, encontramos\(\Lambda_{u b}\) aplicando la Ecuación\(\ref{eqn:16.56}\), que, después de un poco de álgebra, da

\[\Lambda_{u b}=\frac{r_{1} r_{2} r_{3}}{\omega_{b}}=\omega_{b} \frac{c_{\theta}}{J}+\left(\frac{c_{\theta}}{J}\right)^{2}=300 \mathrm{s}}^{-1} \times 100 \mathrm{s}}^{-1}+\left(100 \mathrm{s}}^{-1}\right)^{2}=40,000 \mathrm{s}}^{-2} \nonumber \]

Este resultado para\(\Lambda_{u b}\) es, por supuesto, idéntico al límite superior encontrado por los criterios de Routh en la Ecuación 16.3.13.

Para una aplicación más sutil de este enfoque teórico, vamos: primero, usar Ecuación\(\ref{eqn:16.55}\) para encontrar el valor de los dos polos idénticos en el punto de ruptura, lo cual es evidente en la Figura\(\PageIndex{1}\) (en el eje real, en algún lugar entre el origen y\(-c_{\theta} / J=-100\) s ^-1); y luego, usar Ecuación\(\ref{eqn:16.55}\) para encontrar el valor asociado de\(\Lambda_{b a}\). Es obvio que Ecuación\(\ref{eqn:16.55}\) se satisface de manera idéntica justo en el punto de ruptura, donde\(\theta_{1}=\pi\) y\(\theta_{2}=\theta_{3}=0\), por lo que esto no proporciona ninguna información útil. Pero la Ecuación\(\ref{eqn:16.55}\) debe aplicarse también para todos los demás puntos en los loci de raíces, en particular ahora, para los puntos que están cerca del punto de ruptura; este hecho conducirá a un resultado útil. Supongamos que\(\Lambda\) es apenas un poco mayor\(\Lambda_{b a}\) que para que uno de los polos complejos esté a una pequeña distancia\(\mathcal{E}\) por encima del punto de ruptura en el eje real, como se muestra en el dibujo de abajo. A medida que\(\mathcal{E}\) se contrae pero permanece\(> 0\), los ángulos agudos entre los radios del subsistema y el eje real se vuelven muy pequeños, por lo que podemos usar en Ecuación\(\ref{eqn:16.55}\) la aproximación\(\theta \approx \sin \theta\). Por lo tanto, la ecuación\(\ref{eqn:16.55}\) da

\[\theta_{1}+\theta_{2}+\theta_{3}=\left(\pi-\frac{\varepsilon}{r_{1}}\right)+\frac{\varepsilon}{r_{2}}+\frac{\varepsilon}{r_{3}}=\pi \Rightarrow \varepsilon\left(-\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{3}}\right)=0 \nonumber \]

Esta ecuación debe ser válida aunque\(\mathcal{E}\) sea muy pequeña pero distinta de cero, por lo que concluimos que

\[-\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{3}}=0=\frac{-r_{2} r_{3}+r_{1} r_{3}+r_{1} r_{2}}{r_{1} r_{2} r_{3}} \Rightarrow-r_{2} r_{3}+r_{1} r_{3}+r_{1} r_{2}=0 \nonumber \]

Figura\(\PageIndex{4}\) (Copyright; autor vía fuente)

En el límite a medida que el polo va al punto de ruptura en el eje real\(\varepsilon=0\),, los radios están relacionados como\(r_{1}+r_{2}=c_{\theta} / J\) y\(r_{1}+r_{3}=\omega_{b}\). Sustituyendo en la ecuación anterior para eliminar\(r_2\) y\(r_3\) da\(-r_{2} r_{3}+r_{1}\left(r_{3}+r_{2}\right)=-\left(c_{\theta} / J-r_{1}\right)\left(\omega_{b}-r_{1}\right)+r_{1}\left(\omega_{b}-r_{1}+c_{\theta} / J-r_{1}\right)= 0\), y esto lleva, después de algún álgebra, a una ecuación cuadrática en desconocido\(r_1\):

\[3 r_{1}^{2}-2\left(\omega_{b}+\frac{c_{\theta}}{J}\right) r_{1}+\omega_{b} \frac{c_{\theta}}{J}=0 \nonumber \]

Resolviendo para\(\r_1\) con la fórmula cuadrática da

\[r_{1}=\frac{1}{3}\left[\left(\omega_{b}+\frac{c_{\theta}}{J}\right) \pm \sqrt{\left(\omega_{b}+\frac{c_{\theta}}{J}\right)^{2}-3 \omega_{b} \frac{c_{\theta}}{J}}\right] \nonumber \]

Sustituyendo en esta ecuación\(\omega_{b}=300\) s ^-1 y\(c_{\theta} / J=100\) s-1 da las raíces 221.53 y 45.14 s ^-1, correspondiendo esta última raíz al polo de ruptura que buscamos entre el origen y −100 s ^-1 en el eje real, es decir,\(r_{1}=45.14\) s ^-1. Entonces Ecuación\(\ref{eqn:16.56}\) da el valor asociado del parámetro de control variable:

\[\Lambda_{b a}=\frac{r_{1} r_{2} r_{3}}{\omega_{b}}=\frac{r_{1}\left(c_{\theta} / J-r_{1}\right)\left(\omega_{b}-r_{1}\right)}{\omega_{b}}=2,103.77 \mathrm{s} ^{-2} \nonumber \]

El enfoque utilizado anteriormente para determinar teóricamente los valores de estabilidad de límite superior y ruptura del parámetro de control variable\(\Lambda\), basado en Ecuaciones\(\ref{eqn:16.52}\) -\(\ref{eqn:16.56}\), es una pequeña porción de un extenso conjunto de procedimientos para determinar completamente los loci de raíces, lo que se conoce como el método root-locus. Walter R. Evans (1920-1999, ingeniero eléctrico estadounidense) desarrolló y publicó este elegante método alrededor de 1950. Usando el método root-locus, un ingeniero experimentado puede desarrollar rápidamente, sin la necesidad de una computadora digital, loci completos de raíces, incluso para sistemas de orden algo superior. Durante aproximadamente un cuarto de siglo después de que este método se conociera ampliamente, la regla de cálculo seguía siendo la principal herramienta computacional de un ingeniero, y el método de locus raíz influyó profundamente en el diseño y análisis de sistemas de control durante esa época. Ahora que las computadoras digitales y el software altamente especializado están fácilmente disponibles, el método de locus raíz de Evans ya no es tan esencial si solo necesita analizar un sistema determinado. Sin embargo, si quieres diseñar sistemas de control de manera lógica y eficiente, entonces los conceptos que subyacen al método de Evans, representados en este ejemplo por Ecuaciones\(\ref{eqn:16.52}\)\(\ref{eqn:16.56}\), serán extremadamente valiosos. Los detalles del método de Evans están disponibles en muchas referencias, una de las más claras y completas es Cannon, 1967, Secciones 11.8 y 11.9 y Capítulo 21.

Volvamos ahora a la tarea de elegir un conjunto refinado de\(\Lambda\) valores y usar MATLAB para calcular y graficar loci de raíces para este conjunto refinado. Especificamos que este conjunto consiste en valores para los cuales el sistema es estable,\(0<\Lambda<40,000\) s ^-2, con especial énfasis en el rango de valores asociados al modo oscilatorio dominante de respuesta,\(\Lambda_{b a}<\Lambda<40,000\) s ^-2. Por lo tanto, el valor\(\Lambda_{b a}=2,103.77\) s ^-2 calculado anteriormente es útil, y se incluye en el conjunto refinado de\(\Lambda\) valores. Los otros valores se eligen por ensayo y error para producir un espaciado moderadamente uniforme entre los polos complejos en el\(p\) plano; el conjunto completo, en orden ascendente es\(\Lambda =\) 0, 1,000, 1,800\(\Lambda_{b a}\),, 2,300, 3,500, 6,250, 10,000, 20,000 y 40,000 s ^-2. Excepto por este conjunto diferente de\(\Lambda\) valores, el archivo M de script MATLAB es el mismo que el que produjo Figura\(\PageIndex{1}\). El comando para ejecutar el archivo M, y la salida tabular resultante sigue:

>> MatlabDemo164

Raíces #, Lambda, p

1.0e+004 *

0.0001 0 0 -0.0300 -0.0100

0.0002 0.1000 -0.0305 -0.0083 -0.0012

0.0003 0.1800 -0.0308 -0.0064 -0.0027

0.0004 0.2104 -0.0310 -0.0045 + 0.0000i -0.0045 - 0.0000i

0.0005 0.2300 -0.0311 -0.0045 + 0.0015i -0.0045 - 0.0015i

0.0006 0.3500 -0.0315 -0.0042 + 0.0039i -0.0042 - 0.0039i

0.0007 0.6250 -0.0326 -0.0037 + 0.0066i -0.0037 - 0.0066i

0.0008 1.0000 -0.0337 -0.0031 + 0.0089i -0.0031 - 0.0089i

0.0009 2.0000 -0.0363 -0.0019 + 0.0127i -0.0019 - 0.0127i

0.0010 3.0000 -0.0383 -0.0008 + 0.0153i -0.0008 - 0.0153i

0.0011 4.0000 -0.0400 -0.0000 + 0.0173i -0.0000 - 0.0173i

La gráfica asociada de loci-de-raíces, Figura\(\PageIndex{5}\), se encuentra en la página siguiente. Las características de edición de MATLAB para anotación y mejora gráfica se utilizaron en la Figura\(\PageIndex{5}\). En particular, los ejes se establecieron para ser “iguales”, lo que significa en este caso que el\(x\) eje [es decir,\(\operatorname{Re}(p)\)] y el\(y\) eje [es decir,\(\operatorname{Im}(p)\)] tienen exactamente la misma escala lineal.

Figura\(\PageIndex{5}\): Loci refinados de raíces de Ecuación\(\ref{eqn:16.51a}\) para el parámetro de control variable λ = Kakθ ⁄ J. (Copyright; autor vía fuente)

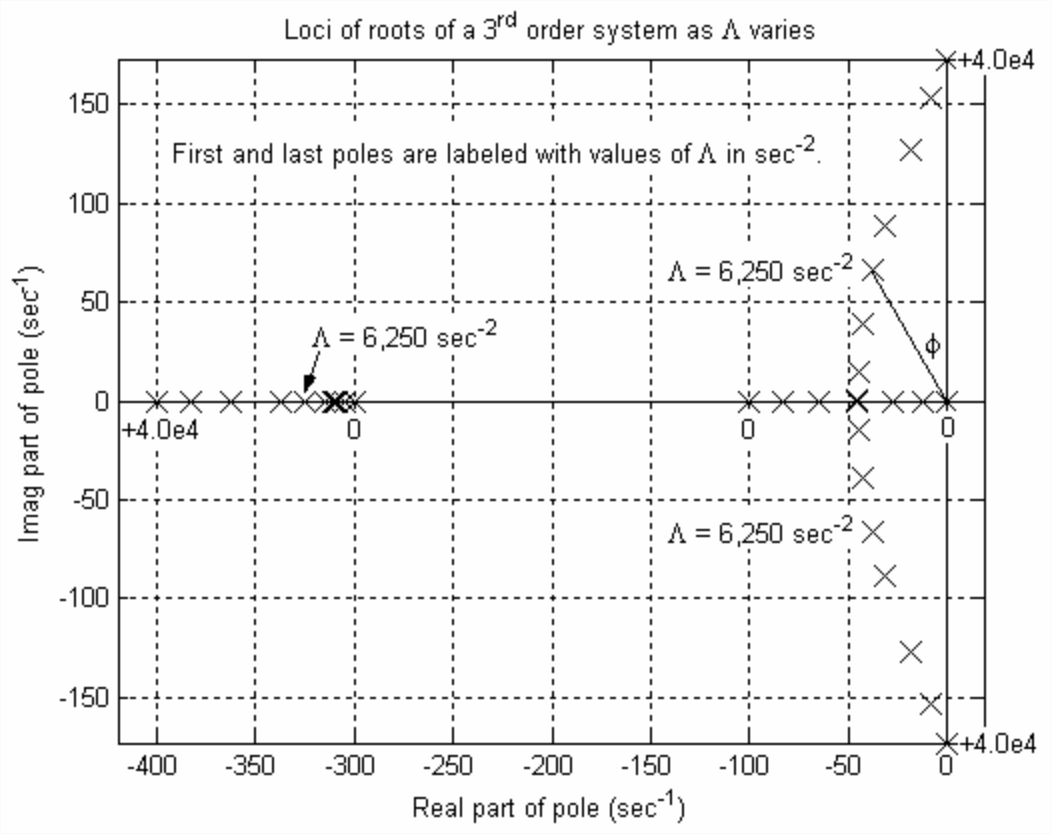
Las raíces de la Figura\(\PageIndex{5}\) para un valor de ejemplo,\(\Lambda=6,250\) s ^-2, se etiquetan con el fin de ilustrar el cálculo de ^los parámetros básicos de primer ^orden y segundo orden para un sistema de orden superior. La raíz real es\(p_{1}=-326\) s ^-1 (tomada aproximadamente de la Figura\(\PageIndex{5}\), pero más precisamente de la tabla de raíces de la página anterior). ^{La constante de tiempo de primer orden asociada es\(\tau_{1}=-1 / p_{1}=3.07 \mathrm{e}-3\) s = 3.07 ms.} Las raíces imaginarias para\(\Lambda=6,250\) s−2 son\(p_{2,3}=-37 \pm j 66\) ^s-1, y el ángulo etiquetado en la Figura\(\PageIndex{5}\) es\(\phi \approx 30^{\circ}\) (por su relevancia, ver Figura\(\PageIndex{5}\)). Los parámetros de respuesta ^{de segundo} orden asociados son: constante de tiempo\(\tau_{2}= -1 / \operatorname{Re}\left(p_{2,3}\right)=27\) ms (mucho más larga que\(\tau_1\)); frecuencia\(\omega_{d}=\operatorname{Im}\left(p_{2}\right)=66\) rad/s; y relación de amortiguación\(\zeta=\sin \phi \approx 0.5\) Podemos utilizar los polos de MATLAB para calcular con mayor precisión la relación de amortiguación asociada a un polo complejo estable,\(p_{k}=\sigma_{k}+j \omega_{k}\) ( la notación de la Sección 16.1), reconociendo que\(\sigma_{k}=\operatorname{Re}\left(p_{k}\right) \equiv-\left(\zeta \omega_{n}\right)_{k}\) y\(\omega_{k}= \operatorname{Im}\left(p_{k}\right) \equiv\left(\omega_{d}\right)_{k}\), y que (dejando temporalmente los\(k\) subíndices)\(\omega_{d}^{2}=\omega_{n}^{2}-\left(\zeta \omega_{n}\right)^{2}\):

\[\zeta^{2}=\frac{\left(\zeta \omega_{n}\right)^{2}}{\omega_{n}^{2}}=\frac{\left(\zeta \omega_{n}\right)^{2}}{\left(\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}} \equiv \frac{\sigma^{2}}{\sigma^{2}+\omega^{2}}=\frac{1}{1+(\omega / \sigma)^{2}} \nonumber \]

Por lo tanto (restaurando los\(k\) subíndices), la relación de amortiguación es

\[\zeta_{k}=\frac{1}{\sqrt{1+\left(\omega_{k} / \sigma_{k}\right)^{2}}}\label{eqn:16.57} \]

Aplicando la Ecuación\(\ref{eqn:16.57}\) para\(\Lambda=6,250\) s ^-2 da\(\zeta_{2}=1 / \sqrt{1+(66 / 37)^{2}}=0.49\).

^{Los cálculos del párrafo anterior sugieren la siguiente pregunta: ¿por qué este sistema de tercer orden tiene un polo real que corresponde a la respuesta exponencial monótona de primer orden, y un par de polos conjugados complejos que corresponden al segundo orden oscilatorio amortiguado} respuesta? De hecho, este es un ejemplo simple de una propiedad general importante de los sistemas lineales invariantes en el tiempo. Cada sistema LTI tiene modos de respuesta asociados con sus polos, las raíces de la ecuación característica del sistema. Esto lo mostramos reescribiendo la ecuación característica de la Ecuación 16.3.1 en la forma factorizada general:

\[\operatorname{Den}(p)=a_{1} p^{n}+a_{2} p^{n-1}+\cdots+a_{n} p+a_{n+1}=a_{1} \prod_{k=1}^{n}\left(p-p_{k}\right)=0\label{eqn:16.58} \]

donde el\(\prod_{k=1}^{n}\) símbolo denota multiplicación de\(n\) términos. Como todos los coeficientes\(a_{k}\) son reales, esta ecuación siempre se puede factorizar en términos ^de primer orden con polos reales y términos ^{de segundo} orden con polos conjugados complejos para los cuales\(\left|\zeta_{j}\right|<1\):

\[\frac{1}{a_{1}} \operatorname{Den}(p)=\prod_{k=1}^{n}\left(p-p_{k}\right)=\ldots\left(p-p_{i}\right) \ldots\left(p^{2}+2 \zeta_{j} \omega_{j} p+\omega_{j}^{2}\right) \ldots\label{eqn:16.59} \]

Podría ser conceptualmente más claro pensar en los modos en términos de respuesta a las condiciones iniciales, sin la complicación de forzar entradas. ^{El modo de respuesta IC asociado a cualquier polo real [\(p_{i}\)en Ecuación\(\ref{eqn:16.59}\)] es exponencial monotónico, exactamente el de un sistema básico de primer orden.} El modo de respuesta IC asociado a cualquier par de polos conjugados complejos [\(-\zeta_{j} \omega_{j} \pm j \omega_{j} \sqrt{1-\zeta_{j}^{2}}\)en Ecuación\(\ref{eqn:16.59}\)] es oscilación modulada por una envolvente exponencial, exactamente la de un sistema básico de ^segundo orden para el cual\(|\zeta|<1\). ^{La respuesta de tiempo total de un sistema LTI a las condiciones iniciales y forzando entradas es la superposición de las respuestas de todos sus modos individuales de primer orden y segundo orden.} Si la respuesta es estable, entonces los mayores contribuyentes a esta respuesta total suelen ser algunos, a lo sumo, modos dominantes, aquellos cuyos polos están más cerca del eje imaginario.

Los modos de vibración introducidos en la Sección 7.6 y el Capítulo 12 representan un caso especial de los modos de respuesta más generales discutidos en el párrafo anterior. Un sistema estructural no amortiguado del tipo considerado en el Capítulo 12 siempre tiene orden par (i.e.,\(n=2,4,6, \ldots\)), de manera que su ecuación característica tiene un número par de raíces. Estas raíces aparecen en pares conjugados puramente imaginarios, cada par para un modo particular de vibración; el valor absoluto de cualquier raíz es la frecuencia natural de ese modo particular.

Antes de continuar, debemos observar una característica general de los diagramas loci-de-raíces. Los polos son reales o, si son complejos, aparecen en pares conjugados, como lo expresa la Ecuación\(\ref{eqn:16.59}\). Por lo tanto, los diagramas loci-de-raíces son siempre simétricos alrededor del\(\operatorname{Re}(p)\) eje. Esta simetría es evidente en las Figuras 16.4.1,\(\PageIndex{1}\), y\(\PageIndex{5}\).