19.3: B.3- Trabajo, Energía y Energía en Circuitos Eléctricos

Los campos eléctricos existen en espacios alrededor y entre partículas cargadas u objetos cargados (Halliday y Resnick, 1960, capítulo 27). La intensidad del campo eléctrico\(\mathcal{E}\) (con unidades SI newton/culombo) en un punto en el espacio es análoga en muchos aspectos a la intensidad del campo gravitacional\(g\), como en la Ec. (B-16). Supongamos que un campo eléctrico está orientado en la\(y\) dirección y es constante. Las mediciones experimentales muestran que la fuerza requerida para sostener una partícula de carga\(q_{p}\) sin aceleración contra el campo eléctrico es

\[f_{y}=q_{p} \mathcal{E}\label{eqn:B.20} \]

(Esta relación lineal es la base para la definición de\(\mathcal{E}\).) Así, la carga\(q_{p}\) dentro de un campo eléctrico de fuerza\(\mathcal{E}\) es análoga a la masa\(m\) dentro de un campo gravitacional de fuerza\(g\). Vemos de esta analogía que el trabajo requerido para mover la carga sin aceleración contra el campo eléctrico se almacena conservadoramente como energía potencial eléctrica:

\[W \equiv E_{E}=\int_{y=y_{1}}^{y=y_{2}} f_{y} d y=\int_{y=y_{1}}^{y=y_{2}} q_{p} \mathcal{E} d y=q_{p} \mathcal{E}\left(y_{2}-y_{1}\right)\label{eqn:B.21} \]

Es habitual y apropiado en teoría eléctrica y aplicaciones definir (en analogía con la diferencia de potencial gravitacional) la diferencia de potencial eléctrico en voltios entre dos puntos en el espacio como (Halliday y Resnick, 1960, Capítulo 29)

\[e_{2}-e_{1} \equiv \mathcal{E}\left(y_{2}-y_{1}\right), \text { or differentially, } d e \equiv \mathcal{E} d y\label{eqn:B.22} \]

Con\(d e \equiv \mathcal{E} d y\) en Ecuación\(\ref{eqn:B.21}\), el trabajo requerido para mover carga\(q_{p}\), trabajo igual a la energía potencial eléctrica, se expresa en términos de diferencia de potencial eléctrico como

\[W \equiv E_{E}=\int_{e=e_{1}}^{e=e_{2}} q_{p} d e=q_{p}\left(e_{2}-e_{1}\right)\label{eqn:B.23} \]

De\(\ref{eqn:B.23}\) la Ecuación inferimos la equivalencia de la unidad SI: 1 voltio = 1 Julio/culombo. Tenga en cuenta las convenciones de signo en la Ecuación\(\ref{eqn:B.23}\): el trabajo y la energía potencial son positivos si una carga positiva\(q_{p}>0\),, se mueve a un mayor potencial eléctrico,\(e_{2}>e_{1}\).

Una aplicación útil de la Ecuación\(\ref{eqn:B.23}\) para la energía potencial eléctrica es a un condensador dentro de un circuito. Halliday y Resnick, 1960, p. 651, explican el proceso físico:

... se debe trabajar para separar dos cargas iguales y opuestas. Esta energía se almacena en el sistema y se puede recuperar si se permite que las cargas vuelvan a juntarse. De igual manera, un condensador cargado tiene almacenada en él una energía potencial eléctrica\(U\) igual al trabajo\(W\) requerido para cargarlo. Esta energía se puede recuperar si se permite que el condensador se descargue. Podemos visualizar el trabajo de carga imaginando que un agente externo extrae electrones de la placa positiva y los empuja sobre la placa negativa, provocando así la separación de carga; normalmente el trabajo de carga lo realiza una batería, a expensas de su almacenamiento de energía química.

Figura\(\PageIndex{1}\) (Copyright; autor vía fuente)

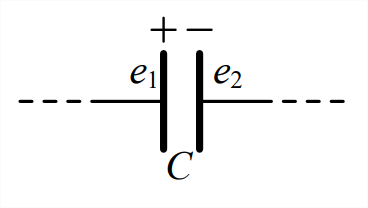
Para derivar una ecuación de energía potencial capacitiva, supongamos que ya se\(q_{+}\) ha transferido alguna cantidad de carga positiva de la placa negativa de un condensador ideal a la placa positiva; la diferencia de voltaje entre las dos placas debido a que\(q_{+}\) se expresa en términos de la capacitancia\(C\), a partir de la Ecuación 5.2.3, as\(e_{1+}-e_{2+}=(1 / C) q_{+}\), en la que\(e_{1+}\) se encuentra un potencial mayor que\(e_{2+}\). De la ecuación\(\ref{eqn:B.23}\), el trabajo diferencial requerido para transferir una cantidad diferencial adicional de carga positiva\(d q_{+}\) de la placa negativa a la placa positiva viene dado por

\[d W=d q_{+}\left(e_{1+}-e_{2+}\right)=\frac{1}{C} q_{+} d q_{+}\label{eqn:B.24} \]

Integramos Ecuación\(\ref{eqn:B.24}\) para encontrar el trabajo total requerido para cargar completamente el condensador ideal de cero a una cantidad\(q\), que también es la energía potencial eléctrica total almacenada en el condensador:

\[W=E_{E}=\int_{q_{+}=0}^{q_{+}=q} d W=\frac{1}{C} \int_{q_{+}=0}^{q_{+}=q} q_{+} d q_{+}=\frac{1}{2} \frac{1}{C} q^{2}\label{eqn:B.25} \]

Mientras que la energía de un condensador\(\ref{eqn:B.25}\), Ecuación, se almacena en un campo eléctrico, la de un inductor se almacena en el campo magnético dentro de las bobinas del inductor; este campo magnético existe como consecuencia de la corriente eléctrica que fluye en el cable (Halliday y Resnick, 1960, Capítulo 34). A pesar de que es energía de campo magnético, todavía podemos aplicar la Ecuación\(\ref{eqn:B.23}\) para el trabajo eléctrico para determinar una ecuación para la energía dentro de un inductor (Halliday y Resnick, 1960, Sección 36-4). De la ecuación\(\ref{eqn:B.23}\), el trabajo diferencial requerido para mover una cantidad diferencial de carga positiva a través de un inductor ideal es

Figura\(\PageIndex{2}\) (Copyright; autor vía fuente)

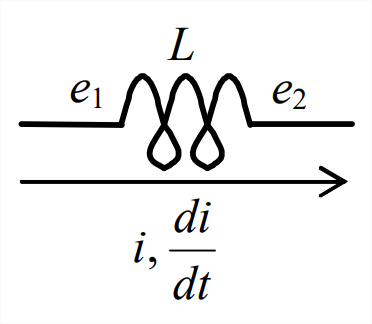
\[d W=d q_{+}\left(e_{1+}-e_{2+}\right)\label{eqn:B.26} \]

en el que\(e_{1+}\) es un potencial mayor que\(e_{2+}\). Este es un proceso conservador, por lo que el trabajo eléctrico, que podría ser realizado por una batería o alguna otra fuente de energía, debe almacenarse como energía de campo magnético,\(E_{M}\). La diferencia de potencial eléctrico autoinducida a través del inductor viene dada por la Ecuación 5.2.9,\(e_{1+}-e_{2+}=L\left(d i_{+} / d t\right)\). También, la corriente y la carga están relacionados por\(i_{+}=d q_{+} / d t\), así que eso\(d q_{+}=i_{+} d t\). Por lo tanto, reescribimos la ecuación\(\ref{eqn:B.26}\) como

\[d W=d E_{M}=i_{+} d t \times L \frac{d i_{+}}{d t}=L i_{+} d i_{+}\label{eqn:B.27} \]

Finalmente, integramos Ecuación\(\ref{eqn:B.27}\) para encontrar la energía potencial magnética total almacenada en el inductor ideal para una cantidad de corriente\(i\):

\[W=E_{M}=L \int_{i_{+}=0}^{i_{+}=i} i_{+} d i_{+}=\frac{1}{2} L i^{2}\label{eqn:B.28} \]

A continuación, aplicamos una vez más la Ecuación\(\ref{eqn:B.23}\) para el trabajo eléctrico con el fin de evaluar fuentes de energía y sumideros de energía en circuitos eléctricos (Halliday y Resnick, 1960, Sección 31-5). Considera un componente general dentro de un circuito, una “caja negra”. Esto podría ser un componente pasivo como una resistencia, una fuente de energía como una batería o un generador de señales, o un dispositivo como un motor que convierte la energía eléctrica en otra forma de energía. Para esta derivación, consideremos que el terminal aguas arriba de la caja negra está a un potencial mayor que el terminal aguas abajo:\(e_1 > e_2\). Supongamos que una carga diferencial positiva\(dq\) se mueve a través de la caja negra de mayor potencial a menor potencial;\(\ref{eqn:B.23}\) La ecuación muestra que hay una reducción de la energía eléctrica:\(d W=d E_{E}=-d q\left(e_{1}-e_{2}\right)=-i d t\left(e_{1}-e_{2}\right)\). La energía eléctrica también se reduce:

\[P_{E}=\frac{d W}{d t}=-i\left(e_{1}-e_{2}\right)\label{eqn:B.29} \]

Figura\(\PageIndex{3}\) (Copyright; autor vía fuente)

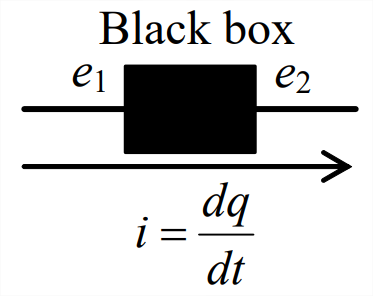
\(\ref{eqn:B.29}\)La ecuación es una fórmula importante que se puede aplicar de manera útil para muchas cajas negras diferentes. Consideraremos aquí sólo dos de ellos. Primero, supongamos que la caja negra es una resistencia con resistencia\(R\), para lo cual la Ecuación 5.2.1 da\(e_{1}-e_{2}=i R\); en este caso, el terminal aguas abajo está a menor voltaje que el terminal aguas arriba, por lo que Ecuación\(\ref{eqn:B.29}\) se convierte en la siguiente fórmula famosa para la energía eléctrica que se disipa en el calentamiento de la resistencia:

\[P_{R}=-i^{2} R\label{eqn:B.30} \]

A continuación, supongamos que la caja negra es una fuente de voltaje de entrada\(e_{i}(t)\) (batería o generador de señal) para un circuito; en este caso, el voltaje aguas abajo\(e_{2}=e_{i}(t)\) excede el voltaje aguas arriba (para corriente positiva\(i\)), por lo que Ecuación\(\ref{eqn:B.29}\) da la fórmula para la energía eléctrica introducida en el circuito por la fuente de voltaje:

\[P_{e}=i\left[e_{i}(t)-e_{1}\right]\label{eqn:B.31} \]

Para la mayoría, si no todos los circuitos relativamente simples considerados en este libro, el terminal aguas arriba de la fuente de voltaje está conectado al potencial de tierra (cero), por lo que\(e_{1} \equiv 0\) y la potencia de entrada es\(P_{e}=i e_{i}(t)\).

Figura\(\PageIndex{4}\) (Copyright; autor vía fuente)

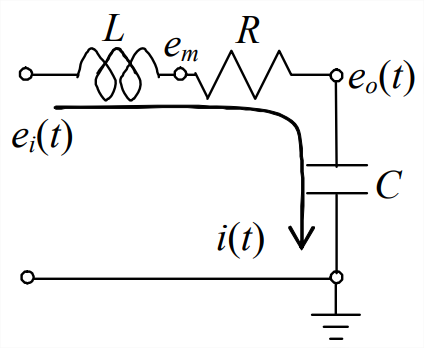
Una interesante aplicación de las ecuaciones derivadas en em esta sección es al\(LRC\) circuito alimentado dibujado arriba, del ejemplo en la Sección 9.2. La energía electromagnética almacenada total reside en el campo eléctrico del condensador ideal y el campo magnético del inductor ideal:

\[E_{E M}=E_{E}+E_{M}=\frac{1}{2} \frac{1}{C} q^{2}+\frac{1}{2} L i^{2}\label{eqn:B.32} \]

El generador de señal es una fuente de energía eléctrica, y la resistencia es un sumidero de energía eléctrica, por lo que la energía electromagnética total varía en el tiempo:

\[\frac{d}{d t} E_{E M}=\frac{d}{d t}\left(\frac{1}{2} \frac{1}{C} q^{2}+\frac{1}{2} L i^{2}\right)=P_{R}+P_{e} \Rightarrow L i \frac{d i}{d t}+\frac{1}{C} q \frac{d q}{d t}=-i^{2} R+i e_{i}(t)\label{eqn:B.33} \]

La cancelación\(i=\dot{q}\) de la ecuación\(\ref{eqn:B.33}\) y la reorganización de los términos conduce al ODE general para la carga\(q(t)\) en las placas del condensador en el\(LRC\) circuito:

\[L \ddot{q}+R \dot{q}+\frac{1}{C} q=e_{i}(t)\label{eqn:B.34} \]

Ya que\(q=C e_{o}\), La ecuación\(\ref{eqn:B.34}\) es esencialmente la misma que la derivada de la ley de voltaje de Kirchhoff en la Sección 9.2 para voltaje de salida\(e_{o}(t)\):\(\ddot{e}_{o}+(R / L) \dot{e}_{o}+(1 / L C) e_{o}=(1 / L C) e_{i}(t)\).