2.4: Impedancia

Debido a que es tan fácil diferenciar una señal de tiempo exponencial compleja, tal forma de representar señales de tiempo tiene ventajas reales en circuitos eléctricos con todo tipo de elementos lineales. En la Sección 1 de estas notas, se introdujo el elemento de resistencia lineal, en el que tensión y corriente están linealmente relacionadas. Ahora debemos considerar otros dos elementos, inductancias y capacitancias. La inductancia produce una relación entre voltaje y corriente que es:

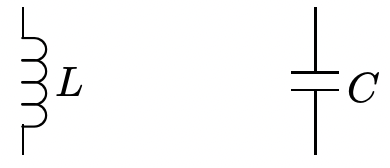Figura 4: Elementos de inductancia y capacitancia

\[\ v_{L}=L \frac{d i_{L}}{d t}\label{35} \]

Si el voltaje y la corriente son funciones sinusoidales del tiempo:

\ (\\ begin {alineado}
v &=\ subrayado {V} e^ {j\ omega t} +\ subrayado {V} ^ {*} e^ {-j\ omega t}\\
i &=\ subrayado {I} e^ {j\ omega t} +\ subrayado {I} ^ {*} e^ {-j\ omega t}
\ end {alineado}\)

Entonces la relación entre voltaje y corriente viene dada simplemente por:

\[\ \underline{V}=j \omega L \underline{I}\label{36} \]

Esta es una forma particularmente simple, y como se puede ver es directamente análoga a la resistencia. Podemos generalizar nuestra visión de la resistencia a la impedancia compleja (o simplemente impedancia), en la que las inductancias tienen impedancia que es:

\[\ \underline{Z}_{L}=j \omega L\label{37} \]

El elemento de capacitancia se define de manera similar. Una capacitancia tiene una relación voltaje-corriente:

\[\ i=C \frac{d v_{C}}{d t}\label{38} \]

Así, la impedancia de una capacitancia es:

\[\ \underline{Z}_{C}=\frac{1}{j \omega C}\label{39} \]

La extensión al comportamiento de la red resistiva es ahora obvia. Para problemas en estado estacionario sinusoidal, en el que todas las excitaciones son sinusoidales, podemos usar todos los trucos del análisis lineal de redes resistivas. Sin embargo, utilizamos impedancia compleja en lugar de resistencia.

La inversa de la impedancia es la admitancia:

\(\ \underline{Y}=\frac{1}{\underline{Z}}\)

Las combinaciones en serie y paralelas de admisiones e impedancias son, por supuesto, igual que las de conductancias y resistencias. Para dos elementos en serie o en paralelo:

Serie:

\[\ \underline{Z}=\underline{Z}_{1}+\underline{Z}_{2}\label{40} \]

\[\ \underline{Y}=\frac{\underline{Y}_{1} \underline{Y}_{2}}{\underline{Y}_{1}+\underline{Y}_{2}}\label{41} \]

Paralelo:

\[\ \underline{Z}=\frac{\underline{Z}_{1} \underline{Z}_{2}}{\underline{Z}_{1}+\underline{Z}_{2}}\label{42} \]

\[\ \underline{Y}=\underline{Y}_{1}+\underline{Y}_{2}\label{43} \]

Ejemplo

Supongamos que vamos a encontrar la tensión\(\ v(t)\) en la red de la Figura 5, en la que\(\ i(t)=I \cos (\omega t)\). La excitación puede escribirse como:

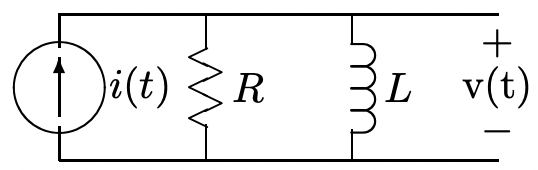Figura 5: Red de impedancia compleja

\(\ i(t)=\frac{I}{2} e^{j \omega t}+\frac{I}{2} e^{-j \omega t}=\operatorname{Re}\left(I e^{j \omega t}\right)\)

Ahora, la impedancia compleja de la combinación paralela de\(\ R\) y\(\ L\) es:

\(\ R \| j \omega L=\frac{R j \omega L}{R+j \omega L}\)

Así que, si\(\ v(t)\) está representado por:

\ (\\ comenzar {alineado}
v (t) &=\ frac {V} {2} e^ {j\ omega t} +\ frac {V} {2} e^ {-j\ omega t}\\
&=R e\ izquierda (\ subrayado {V} e^ {j\ omega t}\ derecha)
\ final {alineado}\)

Entonces

\(\ \underline{V}=\frac{R j \omega L}{R+j \omega L} I\)

Ahora: la impedancia\(\ \underline{Z}\) puede estar representada por una magnitud y un ángulo de fase:

\ (\\ comenzar {alineado}
\ subrayado {Z} &=|\ subrayado {Z} | e^ {j\ phi}\\
|\ subrayado {Z} | &=\ frac {\ omega L R} {\ sqrt {(\ omega L) ^ {2} +R^ {2}}}\
\ phi &=\ frac {\ pi} {2} -\ arctan\ frac {\ omega L} {R}
\ final {alineado}\)

Entonces, utilizando las relaciones desarrolladas aquí,\(\ v(t)\) puede escribirse como:

\(\ v(t)=\frac{\omega L I}{\sqrt{1+\left(\frac{\omega L}{R}\right)^{2}}} \cos (\omega t+\phi)\)

Tenga en cuenta que esta expresión representa solo la solución sinusoidal de estado estacionario, y por lo tanto no representa ningún transitorio inicial.