2.6: Fasores

Los fasores no son armas. Son un truco geométrico práctico que nos ayuda a comprender la naturaleza de las señales y sistemas sinusoidales de estado estacionario. Para comenzar, considere la base para la notación compleja exponencial del tiempo, la función\(\ e^{j \omega t}\). En cualquier instante de tiempo, se trata de un número complejo: en el tiempo\(\ t=0\) es igual a 1, en el tiempo\(\ \omega t=\frac{\pi}{2}\) es igual a\(\ j\), y así sucesivamente. Podemos describir esta función como un vector, de unidad de longitud, que gira alrededor del origen del plano numérico complejo, con velocidad angular\(\ \omega\). Tiene, por supuesto, partes tanto reales como imaginarias, que son solo las proyecciones del vector sobre los ejes real e imaginario.

Ahora considere una señal sinusoidalmente variable\(\ x(t)\), que puede estar representada por:

\(\ x(t)=\frac{X}{2} e^{j \omega t}+\frac{X^{*}}{2} e^{-j \omega t}\)

Esta es la suma de dos números, conjugados complejos, que son, como funciones del tiempo, rotando en direcciones opuestas en el plano complejo. La suma de los dos es, por supuesto, real. Esta es la misma función de tiempo que:

\[\ x(t)=\operatorname{Re}\left(\underline{X} e^{j \omega t}\right)\label{44} \]

donde el operador de parte real\(\ {Re}(\cdot)\) simplemente toma la proyección de la función sobre el eje real.

Podría ser útil en este punto recordar una de las características de la aritmética compleja. La multiplicación de dos números complejos da como resultado un tercer número complejo que tiene:

Figura 7: Programa MATLAB freq.m

1. una magnitud que es producto de las magnitudes de los dos números comienzan a multiplicarse y,
2. un ángulo que es la suma de los ángulos de los dos números que se multiplican.

Así, multiplicar un número por\(\ e^{j \omega t}\), que tiene una magnitud de unidad y un ángulo que va aumentando con el tiempo a la velocidad\(\ \omega\), simplemente tiene el efecto de establecer ese número girando alrededor del origen del plano complejo.

Por lo tanto, es relativamente fácil representar señales que varían sinusoidalmente con solo sus complejas amplitudes, entendiendo que también incluyen\(\ e^{j \omega t}\), lo que proporciona variación de tiempo. La amplitud compleja incluye no sólo la magnitud de la señal, sino también un ángulo de fase. Por lo general, el ángulo de fase por sí mismo es de poca utilidad, y debe estar relacionado con alguna referencia de tiempo. Es decir, como veremos, es la diferencia entre ángulos de fase lo que es importante en la mayoría de los casos.

Las impedancias y las admisiones también son números complejos, por lo que los fasores pueden ser utilizados para visualizar la relación entre tensiones y corrientes en una red. La clave aquí es que la multiplicación y división de números complejos es lo mismo que la multiplicación o división de magnitudes y la suma o resta de ángulos.

Ejemplo

Considere la red simple que se muestra en la Figura 9, y supongamos que la fuente de corriente es sinusoidal:

\(\ i=\operatorname{Re}\left(\underline{I} e^{j \omega t}\right)\)

La impedancia de la combinación R-L es un número complejo:

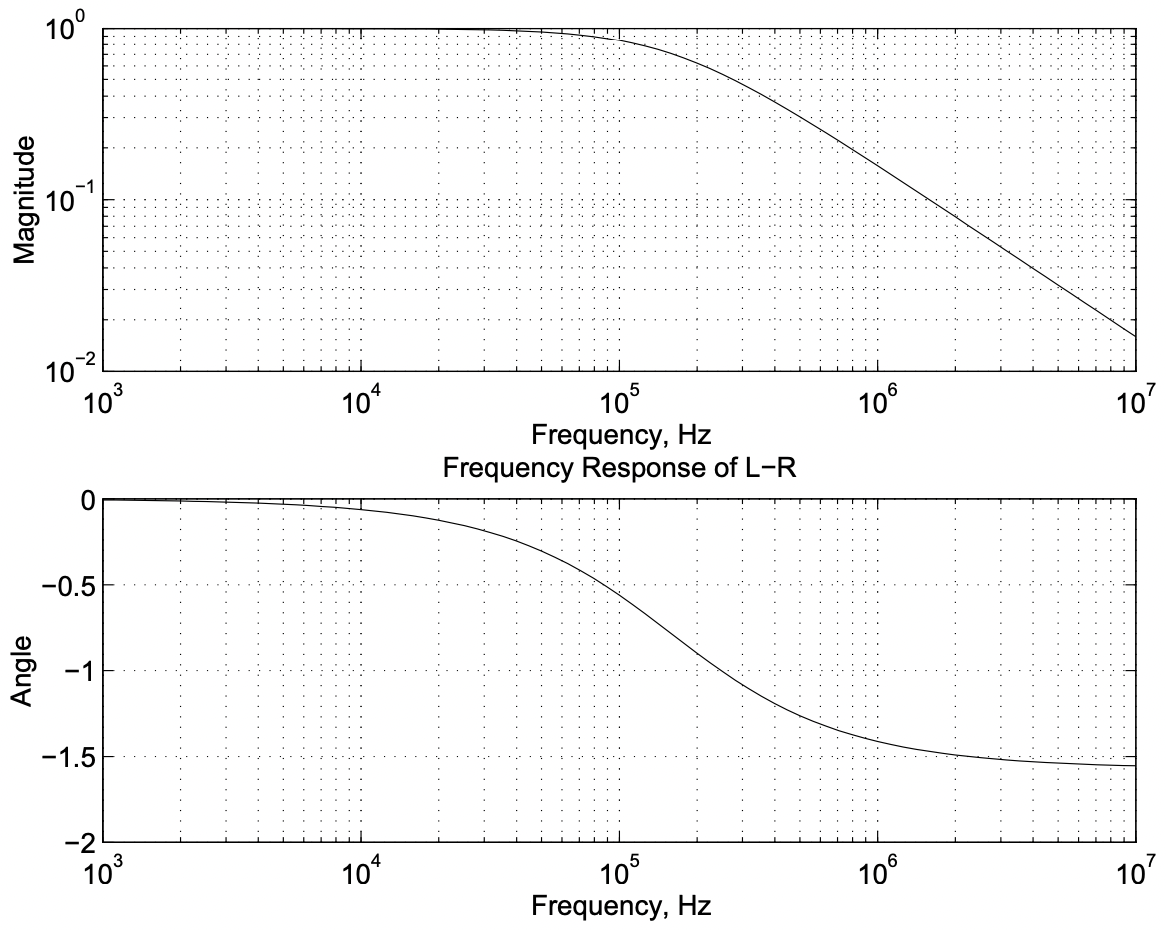Figura 8: Respuesta de frecuencia

\(\ \underline{Z}=R+j \omega L=1+j 2\)

Ahora: la impedancia se puede representar en el plano complejo como se muestra en la Figura 10.

\(\ v\)El voltaje viene dado por:

\(\ v=R e\left(\underline{V} e^{j \omega t}\right)\)

donde:

\(\ \underline{V}=\underline{Z I}\)

Entonces la relación entre voltaje y corriente es como se muestra en la Figura 11. Tenga en cuenta que el ángulo de fase entre voltaje y corriente es el mismo que el ángulo de fase de la impedancia.

Obsérvese que KVL puede representarse gráficamente a la manera de la Figura 12.