2.7: Energía y Poder

Para cualquier par de terminales con voltaje y corriente definidos como se muestra en la Figura 13, el flujo de potencia en el elemento es:

\[\ p=v i\label{45} \]

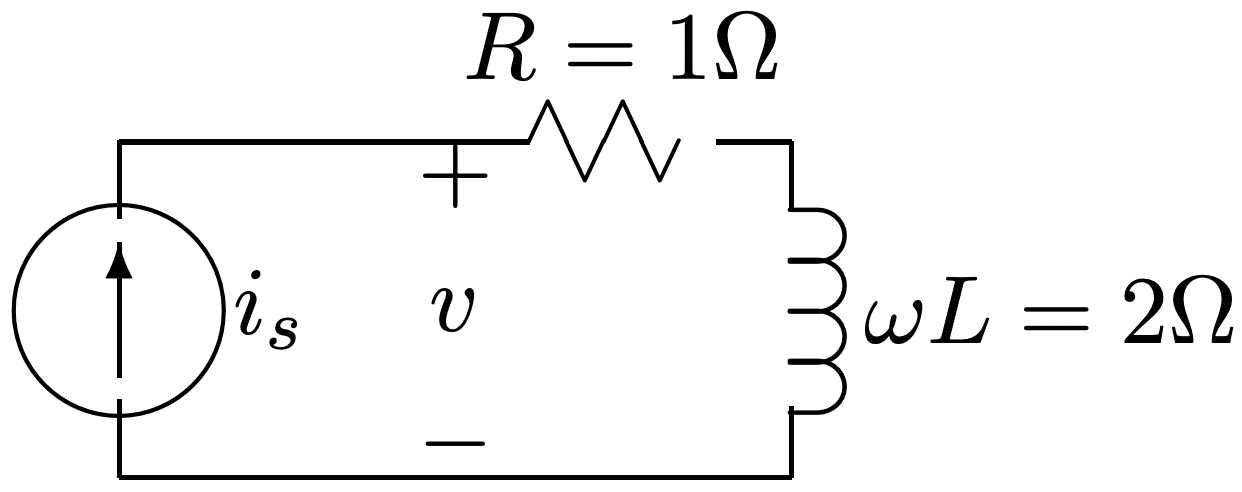Figura 9: Ejemplo de circuito

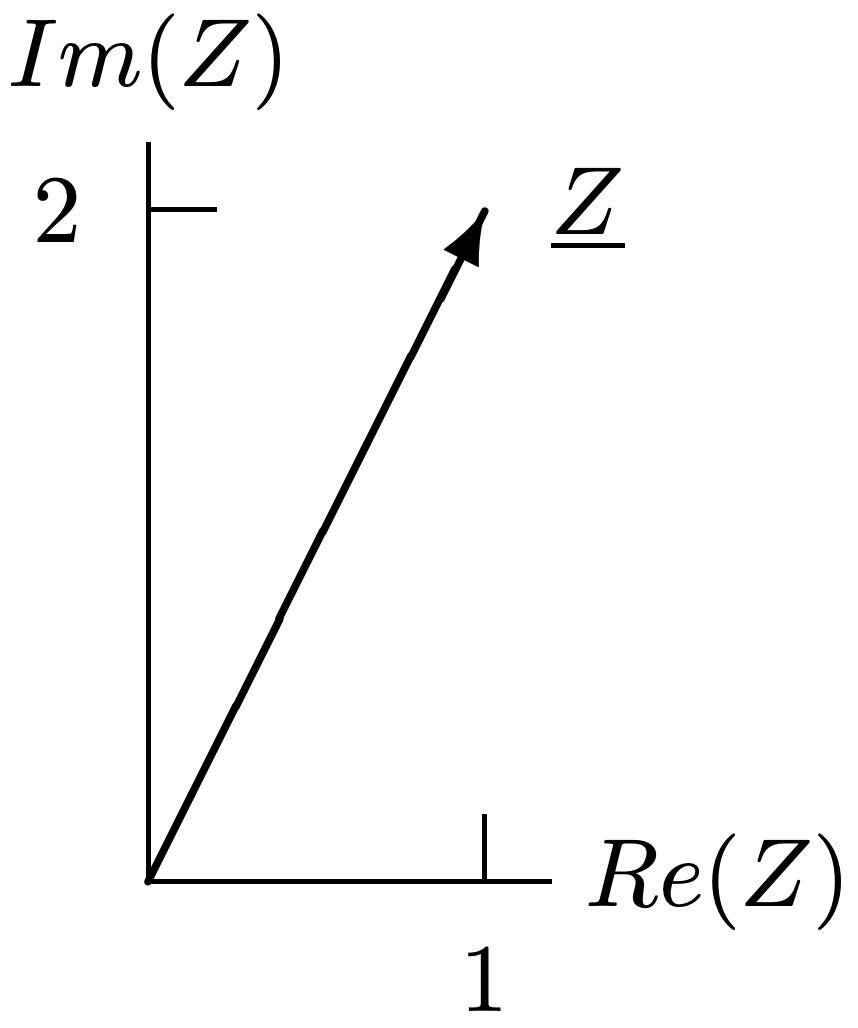Figura 10: Impedancia compleja

La potencia se expresa en Watts (W), y un Watt es el producto de un Voltio y un Amperio. La energía transferida a lo largo de un intervalo de tiempo\(\ t_{0}\) a\(\ t_{1}\) es la integral de la potencia:

\[\ w=\int_{t_{0}}^{t_{1}} v(t) i(t) d t\label{46} \]

La energía se expresa en julios, y un julio es un vatio-segundo. Un Joule también es un Newton-Metro (fuerza por distancia), y por lo tanto un Watt es un Newton-Metro por Segundo.

Consideremos el comportamiento de los tres tipos de elementos lineales pasivos que hemos encontrado:

• \[\ p=R i^{2}=\frac{v^{2}}{R}\label{47} \]

  Figura 11: Voltaje y corriente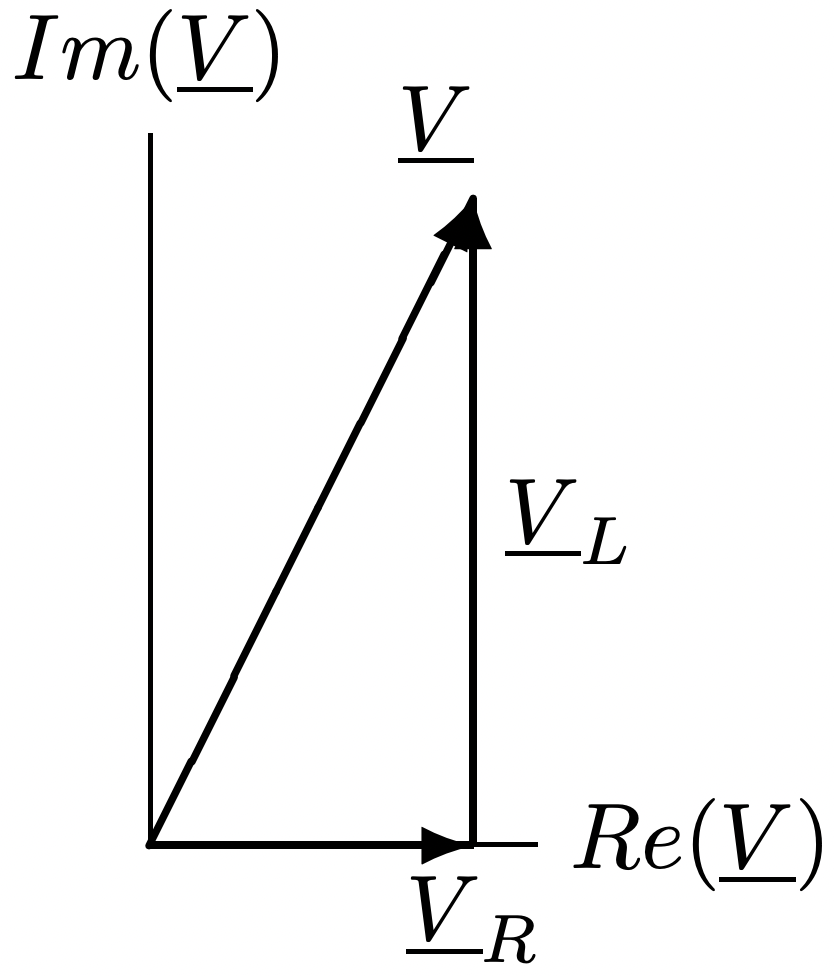

  Figura 12: Componentes de voltaje

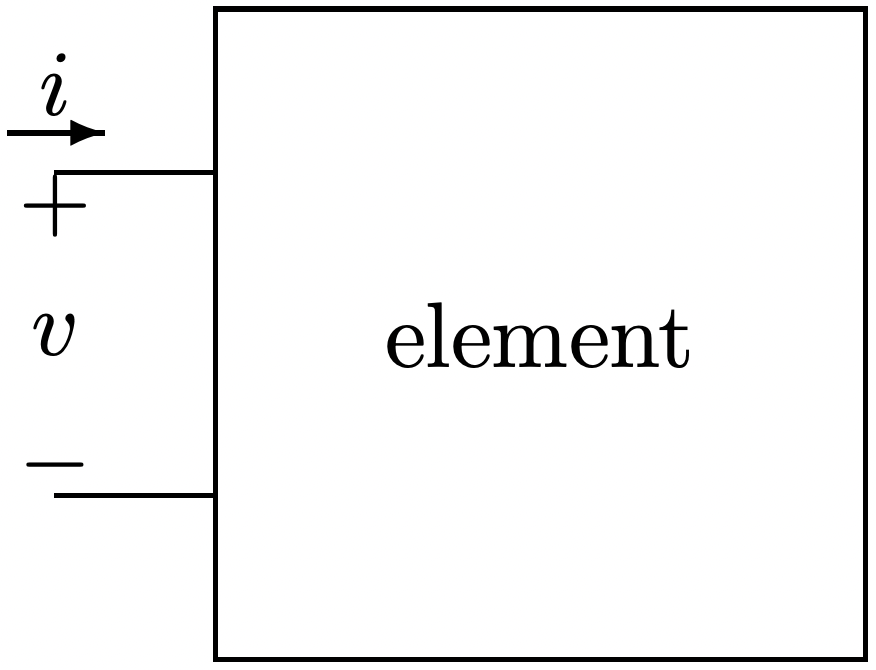  Figura 13: Definición de potencia

• \[\ p=i L \frac{d i}{d t}=\frac{1}{2} L \frac{d i^{2}}{d t}\label{48} \]

  La cantidad\(\ w_{L}=\frac{1}{2} L i^{2}\) puede interpretarse como energía almacenada en la inductancia, de manera que\(\ p=\frac{d w_{L}}{d t}\). Tendremos que afinar esta definición más adelante, cuando consideremos interacciones electromecánicas o elementos no lineales, pero lo hará por ahora.

• \[\ p=v C \frac{d v}{d t}=\frac{1}{2} C \frac{d v^{2}}{d t}\label{49} \]

  La cantidad\(\ w_{C}=\frac{1}{2} C v^{2}\) puede interpretarse de manera similar como energía almacenada en la capacitancia.

  A continuación, considere la entrada de energía a cada uno de estos tres elementos bajo condiciones sinusoidales de estado estacionario:

• Resistencia: si\(\ i=I \cos (\omega t+\theta)\), entonces

  \ [\\ comenzar {alineado}
  p &=R I^ {2}\ cos ^ {2} (\ omega t+\ theta)\\
  &=\ frac {R I^ {2}} {2} [1+\ cos 2 (\ omega t+\ theta)]
  \ final {alineado}\ etiqueta {50}\]

  Así, el poder promedio en la resistencia es:

  \[\ P=\frac{1}{2} R I^{2}\label{51} \]

• Inductancia: si\(\ i=I \cos (\omega t+\theta)\), entonces el voltaje es\(\ v=-\omega L I \sin (\omega t+\theta)\), y la potencia es:

  \ [\\ comenzar {alineado}
  p &=-\ omega L I^ {2}\ cos (\ omega t+\ theta)\ sin (\ omega t+\ theta)\\
  &=-\ frac {\ omega L I^ {2}} {2}\ sin 2 (\ omega t+\ theta)
  \ final {alineado}\ etiqueta {52}\]

  La potencia promedio en la inductancia es cero. La energía instantánea almacenada en la inductancia es

  \(\ w_{L}=\frac{1}{2} L I^{2} \cos ^{2}(\omega t+\theta)\)

  y que tiene un valor promedio:

  \[\ <w_{L}>=\frac{1}{4} L I^{2}\label{53} \]

• \[\ p=-\frac{\omega C V^{2}}{2} \sin 2(\omega t+\phi)\label{54} \]

  que tiene promedio de tiempo cero. La energía almacenada en la capacitancia es:

  \(\ w_{C}=\frac{1}{2} C V^{2} \cos ^{2}(\omega t+\phi)\)

  que tiene promedio de tiempo:

  \[\ <w_{C}>=\frac{1}{4} C V^{2}\label{55} \]

Ahora, considere el flujo de energía hacia un conjunto de terminales en una situación en la que tanto el voltaje como la corriente son sinusoidales y tienen la misma frecuencia, pero posiblemente diferentes ángulos de fase:

\ (\\ comenzar {alineado}
v (t) &=V\ cos (\ omega t+\ phi)\\
i (t) &=I\ sin (\ omega t+\ theta)
\ end {alineado}\)

Es necesario volver a la forma original de notación compleja, como en la ecuación 19, para calcular la potencia.

\[\ v(t)=\frac{1}{2}\left[\underline{V} e^{j \omega t}+\underline{V}^{*} e^{-j \omega t}\right]\label{56} \]

\[\ i(t)=\frac{1}{2}\left[\underline{I} e^{j \omega t}+\underline{I}^{*} e^{-j \omega t}\right]\label{57} \]

La potencia instantánea es producto del voltaje y la corriente:

\[\ p=\frac{1}{4}\left[\underline{V I}^{*}+\underline{V}^{*} \underline{I}+\underline{V I} e^{j 2 \omega t}+\underline{V}^{*} \underline{I}^{*} e^{-j 2 \omega t}\right]\label{58} \]

Esto es directamente equivalente a:

\[\ p=\frac{1}{2} R e\left[\underline{V I}^{*}+\underline{V I} e^{j 2 \omega t}\right]\label{59} \]

Esto es, a su vez, expresable como:

\[\ p=\frac{1}{2}|\underline{V} \| \underline{I}|[\cos (\phi-\theta)+\cos (2 \omega t+\phi+\theta)]\label{60} \]

De esto, extraemos “poder real”, o potencia promedio en el tiempo:

\[\ P=\frac{1}{2} \operatorname{Re}\left[\underline{V I}^{*}\right]=\frac{1}{2}|\underline{V} \| \underline{I}| \cos (\phi-\theta)\label{61} \]

La relación entre el poder real y el poder aparente\(\ P_{a}=\frac{1}{2}|\underline{V} \| \underline{I}|\) se llama factor de potencia, y es simplemente:

\[\ \text { power factor }=\cos \psi=\cos (\phi-\theta)\label{62} \]

El ángulo del factor de potencia\(\ \psi=\phi-\theta\) es el desplazamiento de fase relativo entre voltaje y corriente.

Esta expresión de poder promedio en el tiempo sugiere una definición de algo que podríamos llamar poder complejo:

\[\ P+j Q=\frac{1}{2} \underline{V I}^{*}\label{63} \]

en el que el poder promedio P es la parte real. La magnitud de esta cantidad compleja es el poder aparente. La parte imaginaria se llama potencia reactiva. Tiene importancia que se discutirá más adelante.

Se utilizan diferentes unidades para poder real, reactivo y aparente, con el fin de obtener alguna distinción entre cantidades. Por lo general expresaremos potencia real en watts (W) (o kW, MW,...). La potencia aparente se expresa en volt-amperios (VA), y la potencia reactiva se expresa en voltios-amperios-reactivos (VAR's).

Para obtener más sensación de poder reactivo, expanda la parte variable en el tiempo de la expresión para poder instantáneo:

\(\ p_{\text {varying }}=\frac{1}{2}|\underline{V}||\underline{I}| \cos (2 \omega t+\phi+\theta)\)

Ahora, usando la identidad trig\(\ \cos (x+y)=\cos x \cos y-\sin x \sin y\), y asignando\(\ x=2 \omega t+2 \phi\) y\(\ y=-\psi=\theta-\phi\), tenemos:

\(\ p_{\text {varying }}=\frac{1}{2}|\underline{V} \| \underline{I}|[\cos 2(\omega t+\phi)+\sin \psi \sin 2(\omega t+\phi)]\)

Así, la potencia instantánea total es:

\[\ p=\frac{1}{2}\left|\underline{V}\left\|\underline{I}\left|\cos \psi[1+\cos 2(\omega t+\phi)]+\frac{1}{2}\right| \underline{V}\right\| \underline{I}\right| \sin \psi \sin 2(\omega t+\phi)\label{64} \]

Ahora bien, si observamos expresiones para\(\ P\) y\(\ Q\), podemos reescribir esto como:

\[\ p=P[1+\cos 2(\omega t+\phi)]+Q \sin 2(\omega t+\phi)\label{65} \]

Así, la potencia real P representa no solo la potencia promedio en el tiempo sino también las pulsaciones que van con la potencia promedio en el tiempo. La potencia reactiva Q representa el intercambio de energía con valor promedio cero.

Amplitud RMS

Obsérvese que, en todas las expresiones para poder utilizadas hasta ahora,\(\ \frac{1}{2}\) aparece un factor de. Esto es, por supuesto, porque el valor promedio del producto de dos sinusoides de la misma frecuencia tiene un valor de la mitad de los productos de sus amplitudes pico multiplicado por el coseno del ángulo de fase relativo. Se ha vuelto común usar una medida diferente de amplitud de voltaje, que se llama raíz cuadrática media o simplemente RMS. La definición adecuada para el valor RMS de una forma de onda es algo compleja, pero se reduce a ese valor que, si fuera CC, disiparía la misma potencia en una resistencia. Es posible definir RMS para cualquier forma de onda periódica. Sin embargo, como vamos a estar tratando con sinusoides, la definición es aún más fácil. Claramente, dado que la potencia disipada en una resistencia es, en términos de amplitudes de pico:

\(\ P=\frac{1}{2} \frac{|\underline{V}|^{2}}{R}\)

entonces la amplitud RMS debe ser:

\[\ V_{R M S}=\frac{|\underline{V}|}{\sqrt{2}}\label{66} \]

Entonces,

\(\ P=\frac{V_{R M S}^{2}}{R}\)

Como veremos, las amplitudes RMS son las predeterminadas para la mayoría de las situaciones: cuando un circuito se describe como “120 Volts AC”, la designación prácticamente siempre significa 120 Volts, RMS. La amplitud máxima de esta es\(\ |\underline{V}|=\sqrt{2} \cdot 120 \approx 170\) voltios. A menudo verá formas de onda sinusoidales expresadas en la forma:

\(\ v=\sqrt{2} V_{R M S} \cos (\omega t)\)

en el que V _RMS es obviamente la amplitud RMS

Ejemplo

Considera la sencilla red de la Figura 14. Calcularemos el flujo instantáneo de energía hacia esa red en términos que hemos estado discutiendo. Supongamos que la fuente de voltaje tiene amplitud RMS

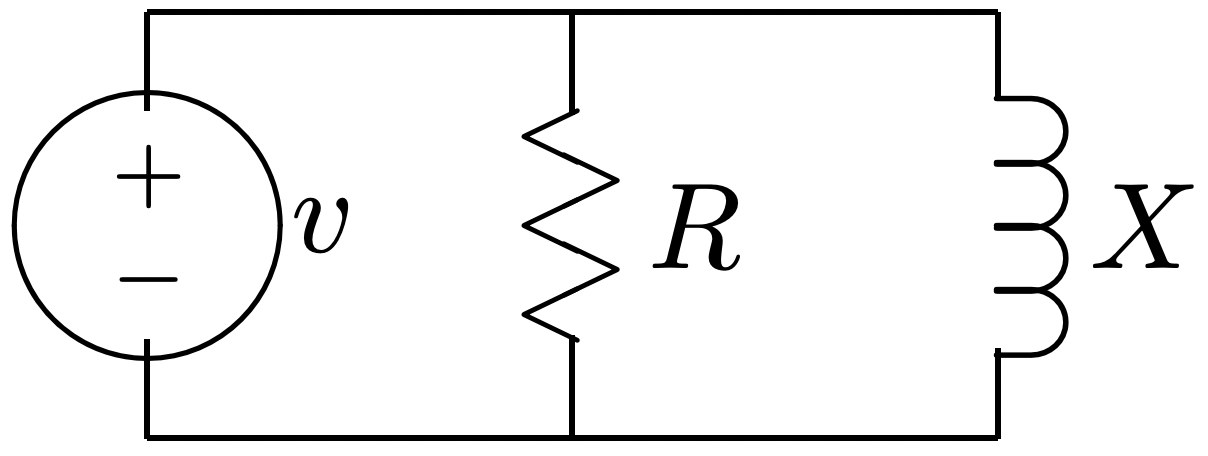Figura 14: Ejemplo de circuito

de 120 voltios y\(\ R\) y\(\ X\) son ambos de 100 Ω. Entonces:

\(\ v(t)=170 \cos \omega t\)

La admisión de esta red es:

\(\ Y=\frac{1}{100}-\frac{j}{100}\)

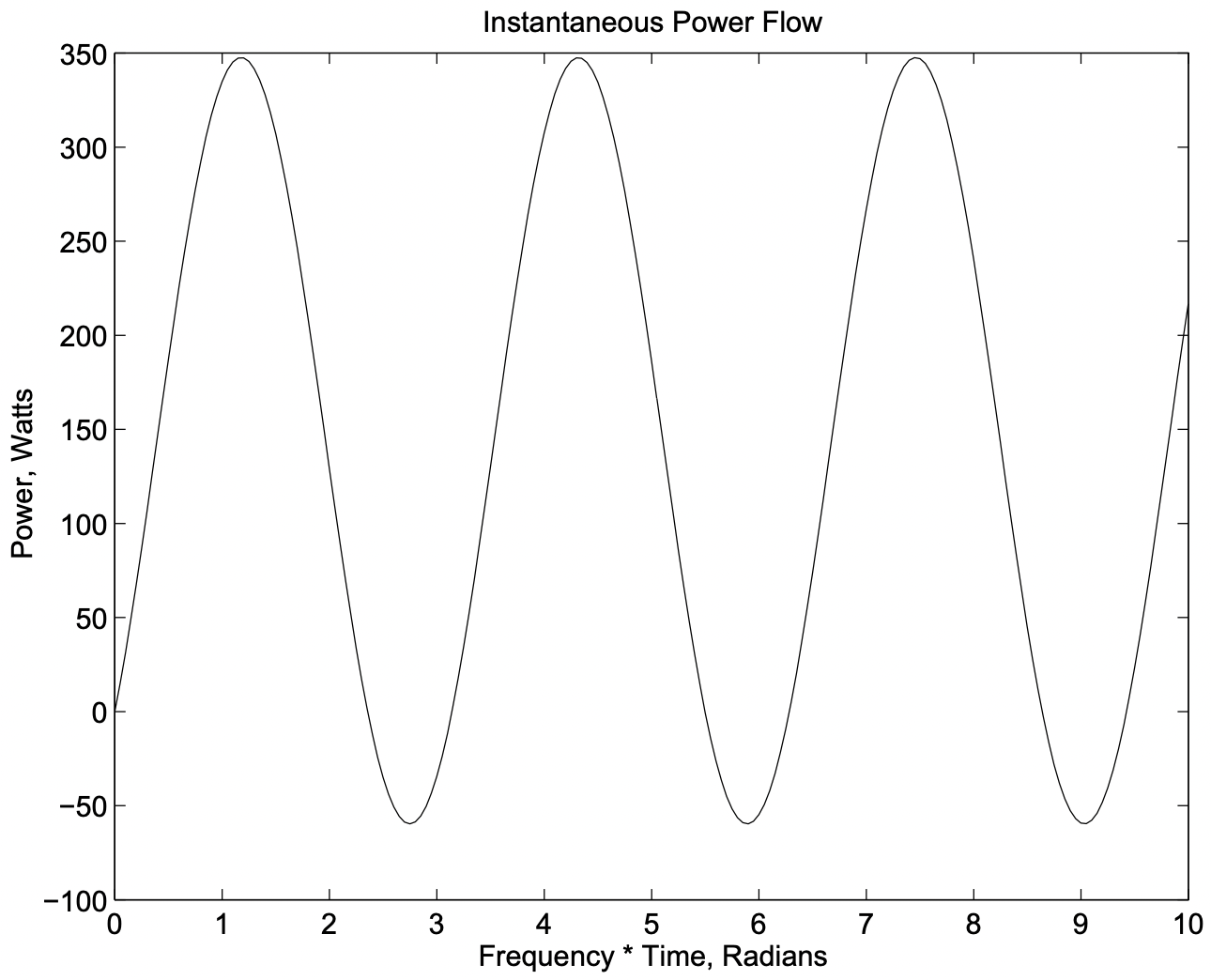Figura 15: Flujo de potencia para circuito de ejemplo

de manera que la amplitud compleja de la corriente sea:

\(\ I=1.7-j 1.7\)

Y entonces el poder complejo es:

\(\ P+j Q=\frac{1}{2} 170(1.7+j 1.7)\)

La potencia real y reactiva son, respectivamente:\(\ P=144 \mathrm{~W}\),\(\ Q=144 \mathrm{VAR}\). Esto da un ángulo de factor de potencia de\(\ \psi=\arctan (1)=45^{\circ}\). Entonces, la potencia instantánea es:

\(\ p=144\left[1+\cos 2\left(\omega t-45^{\circ}\right)\right]+144 \sin 2\left(\omega t-45^{\circ}\right)\)

Esto se ilustra en la Figura 15.