2.9: Flujo de potencia a través de una impedancia

Considera la situación que se muestra en la Figura 16. Esto en realidad representa una serie de situaciones importantes en los sistemas de energía, donde la impedancia\(\ \underline{Z}\) podría representar una línea de transmisión, transformador o devanado del motor. De interés para nosotros es el flujo de potencia a través de la impedancia. Se da corriente

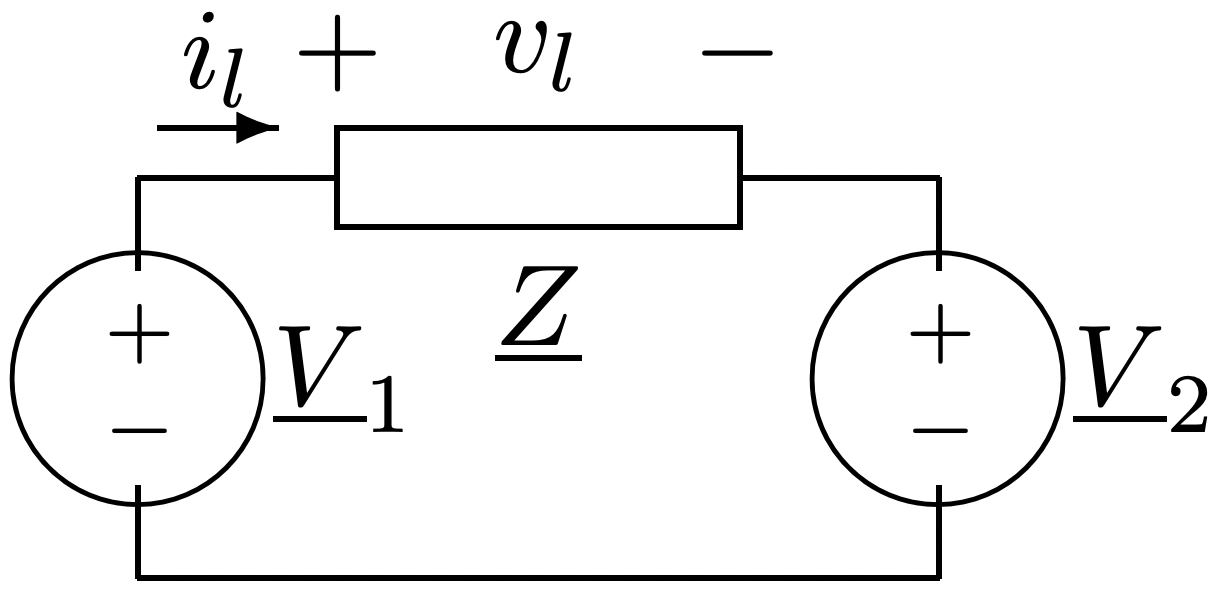Figura 16: Ejemplo de flujo de potencia

por:

\[\ \underline{i_{l}}=\frac{\underline{V}_{1}-\underline{V}_{2}}{\underline{Z}}\label{72} \]

Entonces, el flujo de energía complejo que sale de la fuente de voltaje de la izquierda es:

\[\ P+j Q=\frac{1}{2} \underline{V}_{1}\left(\frac{\underline{V}_{1}^{*}-\underline{V}_{2}^{*}}{\underline{Z}^{*}}\right)\label{73} \]

Ahora, las amplitudes complejas pueden expresarse como:

\[\ \underline{V}_{1}=\left|\underline{V}_{1}\right| e^{j \theta}\label{74} \]

\[\ \underline{V}_{2}=\left|\underline{V}_{2}\right| e^{j \theta+\delta}\label{75} \]

donde\(\ \delta\) es el ángulo de fase relativo entre las dos fuentes de voltaje. La potencia compleja en los terminales de la fuente de voltaje ahora\(\ \underline{V}_{1}\) viene dada por:

\[\ P+j Q=\frac{\left|\underline{V}_{1}\right|^{2}}{2 \underline{Z}^{*}}-\frac{\left|\underline{V}_{1}\right|\left|\underline{V}_{2}\right| e^{-j \delta}}{2 \underline{Z}^{*}}\label{76} \]

Esto es descriptible como un círculo en el plano complejo, con su origen en

\(\ \frac{\left|\underline{V}_{1}\right|^{2}}{2 \underline{Z}^{*}}\)

y su radio igual a:

\(\ \frac{\left|\underline{V}_{1}\right|\left|\underline{V}_{2}\right|}{2|\underline{Z}|}\)

Ahora supongamos que la impedancia a través de la cual estamos pasando la potencia es descriptible como una inductancia simple como se muestra en la Figura 17. Este es quizás el más simple de los modelos de línea de transmisión que representa solo la impedancia inductiva de la línea. La inductancia de línea surge porque las corrientes en la línea producen campos magnéticos, y este es un modelo justo para la mayoría de las líneas que son bastante 'cortos'. Más sobre eso en la siguiente sección. Esta línea tiene la impedancia

\(\ Z=j \omega L=j X_{L}\)

Ahora, cambiando a amplitudes RMS, de modo que\(\ \underline{V}_{s}=\sqrt{2} \underline{V}_{1}\) y\(\ \underline{V}_{r}=\sqrt{2} \underline{V}_{2}\), Entonces el flujo de potencia real y reactivo son:

\ (\\ begin {alineado}
P_ {s} +j Q_ {s} &=\ subrayado {V} _ {s}\ subrayado {I} ^ {*} =j\ frac {\ izquierda|v_ {s}\ derecha|^ {2} -\ subrayado {V} _ {s}\ subrayado {V} _ _ {r} ^ {*} {X_ {l}}\\
P_ {r} +j Q_ {r} &=-\ subrayado {V} _ {r}\ subrayado {I} ^ {*} =j\ frac {\ izquierda|v_ {r}\ derecha|^ {2} -\ subrayado {V} _ _ {s} ^ {*}\ subrayado {V} _ {r }} {X_ {l}}
\ final {alineado}\)

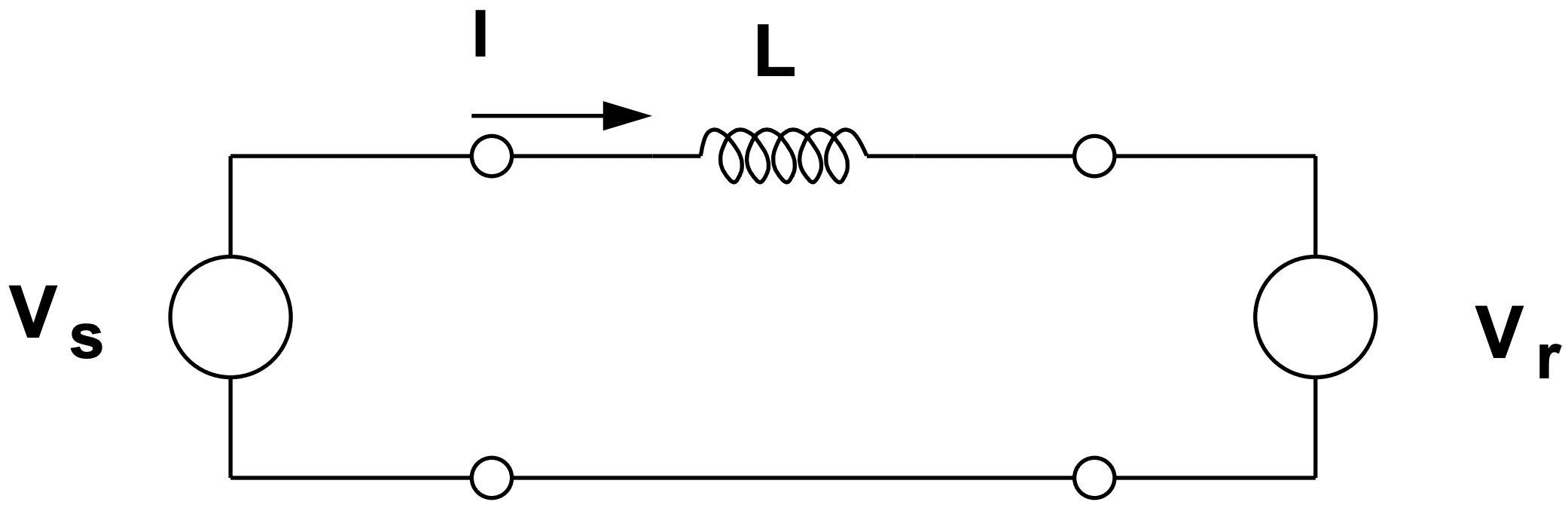Figura 17: Modelo de línea de transmisión más simple

Ahora si asumimos que los voltajes son de la forma:

\ (\\ begin {array} {l}
\ subrayado {V} _ {s} =V_ {s} e^ {j\ phi}\
\ subrayado {V} _ {r} =V_ {r} e^ {j\ theta}
\ end {array}\)

y que el ángulo de fase relativo entre ellos es\(\ \phi-\theta=\delta\) y haciendo un poco trig:

\ (\\ comenzar {alineado}
P_ {s} &=\ frac {V_ {s} V_ {r}\ sin\ delta} {X_ {L}}\\
Q_ {s} &=\ frac {V_ {s} ^ {2} -V_ {s} V_ {r}\ cos\ delta} {X_ {L}}\
P_ {r} =-\ frac {V_ {s} V_ {r}\ sin\ delta} {X_ {L}}\\
Q_ {r} &=\ frac {V_ {r} ^ {2} -V_ {s} V_ {r}\ cos\ delta} {X_ {L}}
\ end {alineado}\)

Una imagen de este locus se conoce como diagrama de círculo de potencia, debido a su forma. La figura 18 muestra la construcción de un diagrama de círculo de potencia final de envío para tensiones iguales de extremo de envío y de recepción y una impedancia puramente reactiva.

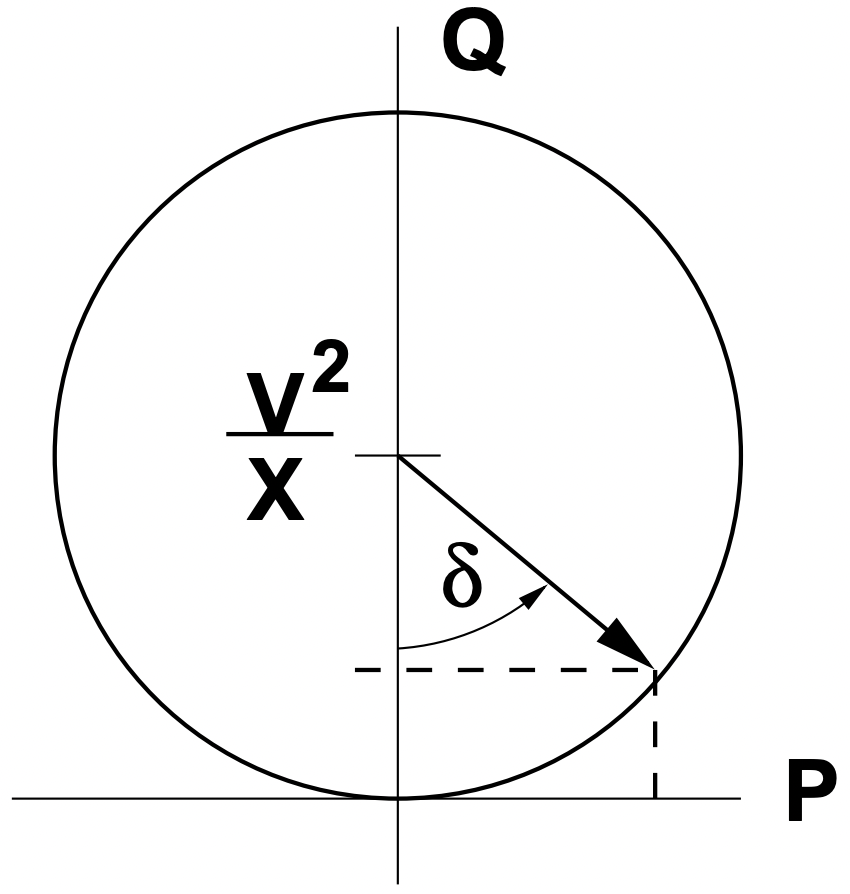Figura 18: Círculo de potencia, voltajes iguales

Como comprobación, considere la potencia reactiva consumida por la propia línea: esperamos eso\(\ Q_{s}+Q_{r}=Q_L\), y así:

\(\ Q_{s}+Q_{r}=\frac{V_{s}^{2}+V_{r}^{2}-2 V_{s} V_{r} \cos \delta}{X_{L}}\)

Tenga en cuenta que el voltaje a través del elemento de línea en sí se encuentra usando la ley de los cosenos (ver Figura 19:

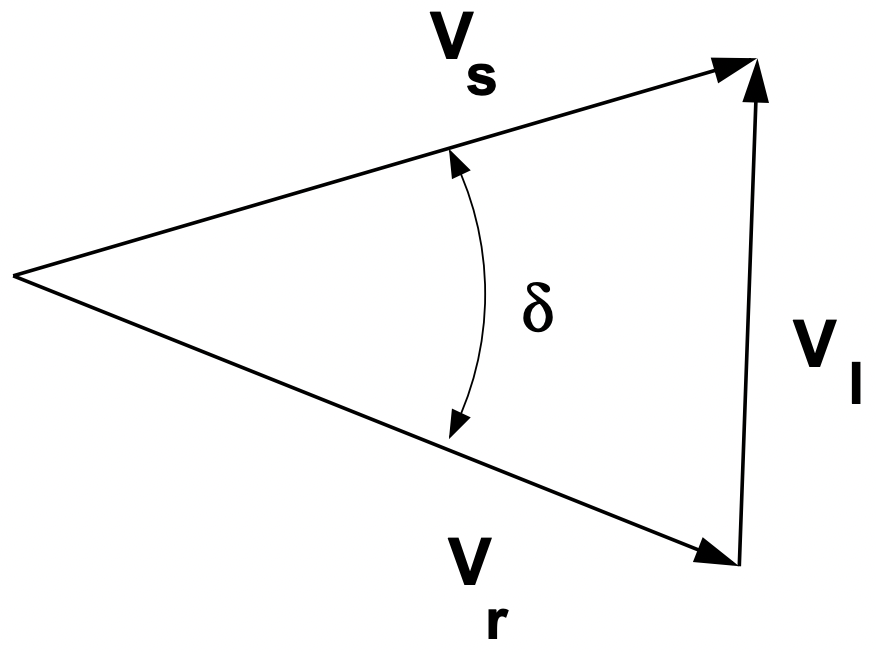Figura 19: Ilustración de la Ley de Cosinos

\(\ V_{L}^{2}=V_{s}^{2}+V_{r}^{2}-2 V_{s} V_{r} \cos \delta\)

y, de hecho,

\(\ Q_{L}=\frac{V_{L}^{2}}{X_{L}}\)