5.4: Bloqueo de modo activo con SPM adicional
- Page ID
- 84809
Debido al fuerte enfoque del pulso en el medio de ganancia también puede llegar a ser importante la modulación de autofase adicional. Consideremos el caso de un láser activamente bloqueado en modo con SPM adicional, ver Figura 5.7. Se puede anotar la ecuación maestra correspondiente
\[T_R \dfrac{\partial A}{\partial T} = \left [g(T) + D_g \dfrac{\partial^2}{\partial t^2} - l - M_s t^2 - j \delta |A|^2 \right ] A.\label{eq5.4.1} \]
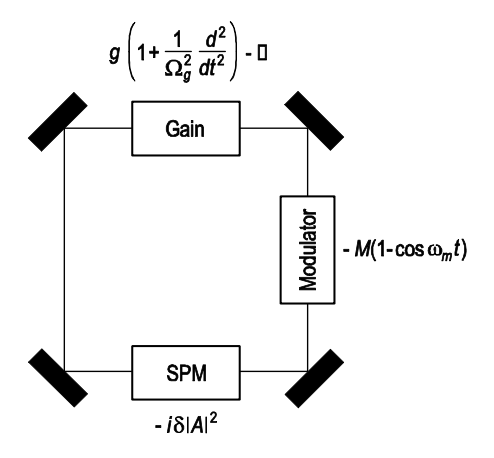
Desafortunadamente, no hay solución analítica a esta ecuación. Pero no es difícil adivinar qué pasará en este caso. Mientras el SPM no sea excesivo, los pulsos experimentarán modulación de autofase adicional, lo que crea un chirp en el pulso. Así se puede hacer un ansatz con un gaussiano chirped similar a (5.3.4) para la solución de estado estacionario de la ecuación maestra (\(\ref{eq5.4.1}\))
\[A_0 (t) = Ae^{-\tfrac{t^2}{2\tau_a^2} (1 + j \beta) j \Psi T/T_R} \nonumber \]
Tenga en cuenta que permitimos un desplazamiento de fase adicional por ida y vuelta\(\Psi\), ya que el SPM agregado no deja la fase invariante después de un viaje de ida y vuelta. Esta sigue siendo una solución de estado estacionario para la envolvente de intensidad. Sustitución en la ecuación maestra usando el resultado intermedio
\[\dfrac{\partial ^2}{\partial t^2} A_0 (t) = \left \{\dfrac{t^2}{\tau_a^4} (1 + j\beta)^2 - \dfrac{1}{\tau_a^2} (1 + j \beta) \right \} A_0 (t). \nonumber \]
lleva a
\[j \Psi A_0 (t) = \left \{g - l + D_g \left [\dfrac{t^2}{\tau_a^4} (1 + j\beta)^2 - \dfrac{1}{\tau_a^2} (1 + j \beta) \right ] - M_s t^2 - j \delta |A|^2 e^{-\tfrac{t^2}{\tau_a^2}} \right \} A_0 (t). \nonumber \]
Para encontrar una solución aproximada ampliamos el gaussiano en el paréntesis, lo que es una consecuencia del SPM a primer orden en el exponente.
\[j \Psi = g- l + D_g \left [\dfrac{t^2}{\tau_a^4} (1 + j\beta)^2 - \dfrac{1}{\tau_a^2} (1 + j \beta) \right ] - M_s t^2 - j \delta |A|^2 \left (1 - \dfrac{t^2}{\tau_a^2} \right ). \nonumber \]
Esto tiene que cumplirse para todos los tiempos, por lo que podemos comparar coeficientes frente a los términos constantes y los términos cuadráticos, lo que lleva a dos condiciones complejas. Esto lleva a cuatro ecuaciones para el ancho de pulso desconocido, el chirrido\(\tau_a\)\(\beta\), la fase de ida y vuelta\(\Psi\) y el exceso de ganancia necesario\(g - l\). Con el desplazamiento de fase pico no lineal debido a SPM,\(\phi_0 = \delta |A|^2\). Las partes reales e imaginarias de los términos cuadráticos conducen a
\[0 = \dfrac{D_g}{\tau_a^4} (1 - \beta^2) - M_s, \nonumber \]
\[0 = 2 \beta \dfrac{D_g}{\tau_a^4} + \dfrac{\phi_0}{\tau_a^2}, \nonumber \]
y los términos constantes dan el exceso de ganancia y la fase adicional de ida y vuelta.
\[g - l = \dfrac{D_g}{\tau_a^2}, \nonumber \]
\[\Psi = D_g \left [-\dfrac{1}{\tau_a^2} \beta \right ] - \phi_0. \nonumber \]
Las dos primeras ecuaciones dan directamente el chirp y el ancho de pulso.
\[\beta = -\dfrac{\phi_0 \tau_a^2}{2D_g} \nonumber \]
\[\tau_a^4 = \dfrac{D_g}{M_s + \tfrac{\phi_0^2}{4D_g}}. \nonumber \]
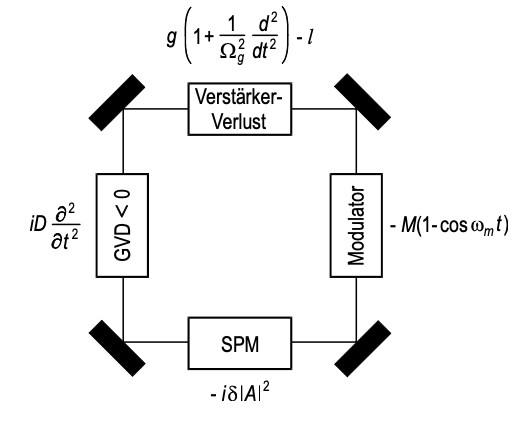
No obstante, hay que señalar, que este simple análisis no da ninguna pista sobre la estabilidad de estas soluciones aproximadas. De hecho, las simulaciones por computadora muestran, que después de un cortocircuito de pulso adicional de aproximadamente un factor de 2 por SPM más allá del ancho de pulso ya logrado por el bloqueo de modo activo puro por sí solo, el SPM impulsa los pulsos inestables [5]. Esta es una de las razones, por qué los medios láser de muy banda ancha, como TI:Sapphire, no pueden simplemente generar pulsos de femtosegundos mediante medolocking activo. El SPM que ocurre en el medio de ganancia para pulsos muy cortos impulsa el modelocking inestable. Se tienen que adoptar medidas adicionales de estabilización. Por ejemplo, la adición de dispersión de retardo de grupo negativo podría conducir a la formación estable de solitones en presencia del modelocker activo.