4.2: Impedancia de un Cable
- Page ID
- 83884
El objetivo de esta sección es determinar la impedancia —la relación entre el potencial y la corriente— de un cable. La respuesta a esta pregunta es relativamente simple en el caso de CC (“corriente constante”): Se encuentra que la impedancia es igual a la resistencia del cable, que viene dada por
\[R = \frac{l}{\sigma A} ~~~~~\mbox{(DC)} \label{m0159_eRW} \]
donde\(l\) es la longitud del cable y\(A\) es el área de la sección transversal del cable. Además, la impedancia de un cable compuesto por un conductor perfecto a cualquier frecuencia es simplemente cero, ya que no hay ningún mecanismo en el cable que pueda disipar o almacenar energía en este caso.
Sin embargo, todos los cables prácticos están compuestos por conductores buenos, no perfectos, y por supuesto muchas señales prácticas varían en el tiempo, por lo que los dos casos anteriores no abordan una amplia categoría de interés práctico. El caso más general de corrientes no estables en conductores imperfectos se complica por el hecho de que la corriente en un conductor imperfecto no se distribuye uniformemente en el cable, sino que se concentra cerca de la superficie y decae exponencialmente al aumentar la distancia desde la superficie (esto se determina en Sección 4.1).
Ahora estamos listos para considerar la caja de CA para un cable compuesto por un conductor bueno pero imperfecto. ¿Cuál es la impedancia del cable si la fuente de corriente es sinusoidalmente variable? La ecuación\ ref {M0159_ERW} para el caso de CC se determinó obteniendo primero expresiones para el potencial (\(V\)) y la corriente neta (\(I\)) para una\(l\) sección de longitud de cable en términos de la intensidad del campo eléctrico\({\bf E}\) en el cable. Para seguir ese mismo enfoque aquí, requerimos una expresión para\(I\) en términos de\({\bf E}\) que da cuenta de la distribución no uniforme de la corriente. Esto es bastante difícil de determinar en el caso de un alambre cilíndrico. Sin embargo, podemos desarrollar una solución aproximada considerando una superficie que no es cilíndrica, sino plana. Aquí vamos:
Considera el experimento descrito en la Figura\(\PageIndex{1}\).
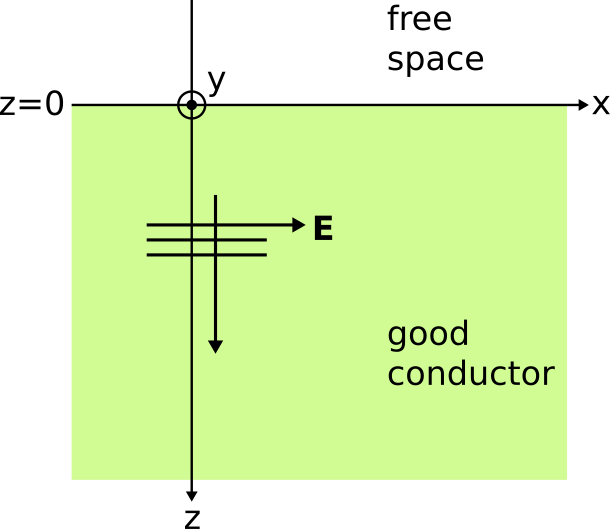
Aquí, una región semi-infinita llena de un buen conductor homogéneo se encuentra con una región semi-infinita de espacio libre a lo largo de una interfaz plana en\(z=0\), con el aumento\(z\) correspondiente al aumento de la profundidad en el material. Una onda plana se propaga en la\(+\hat{\bf z}\) dirección, comenzando desde justo dentro de la superficie de la estructura. La justificación para presumir la existencia de esta ola se presentó en la Sección 4.1. La intensidad del campo eléctrico viene dada por
\[\widetilde{\bf E} = \hat{\bf x}E_0 e^{-\alpha z} e^{-j\beta z} \nonumber \]
donde\(E_0\) es una constante arbitraria de valor complejo. La densidad de corriente está dada por la ley de electromagnetismo de Ohm: 1
\[\widetilde{\bf J} = \sigma\widetilde{\bf E} = \hat{\bf x}\sigma E_0 e^{-\alpha z} e^{-j\beta z} \label{m0159_eJ} \]
Recordemos que\(\alpha = \delta_s^{-1}\) dónde\(\delta_s\) está la profundidad de la piel (ver Sección 3.12). También, para un buen director, lo sabemos\(\beta \approx \alpha\) (Sección 3.11). Usando estas relaciones, podemos reescribir la Ecuación\ ref {M0159_eJ} de la siguiente manera:
\[\begin{align} \widetilde{\bf J} &\approx \hat{\bf x}\sigma E_0 e^{-z/\delta_s} e^{-jz/\delta_s} \nonumber \\ &= \hat{\bf x}\sigma E_0 e^{-(1+j)z/\delta_s} \end{align} \nonumber \]
La corriente neta\(\widetilde{I}\) se obtiene integrando\(\widetilde{\bf J}\) sobre cualquier sección transversal\(\mathcal{S}\) a través de la cual fluye toda la corriente; es decir,
\[\widetilde{I} = \int_{\mathcal{S}} \widetilde{\bf J}\cdot d{\bf s} \nonumber \]
Aquí, la solución más simple se obtiene eligiendo\(\mathcal{S}\) ser una superficie rectangular que sea perpendicular a la dirección de\(\widetilde{\bf J}\) at\(x=0\). Esto se muestra en la Figura\(\PageIndex{2}\).
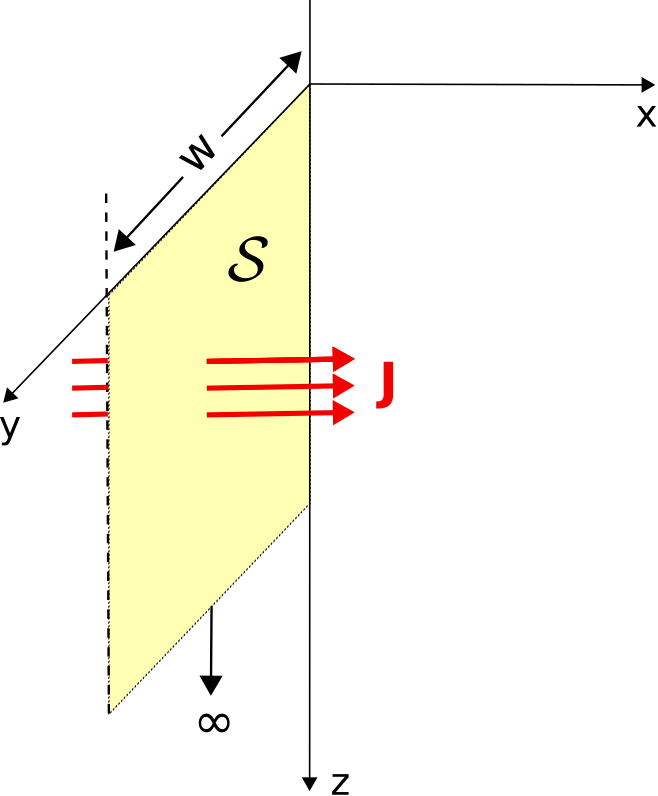
Las dimensiones de\(\mathcal{S}\) son ancho\(W\) en la\(y\) dimensión y extendiéndose hasta el infinito en la\(z\) dirección. Entonces tenemos
\[\begin{align} \widetilde{I} &\approx \int_{y=0}^{W} \int_{z=0}^{\infty} \left( \hat{\bf x}\sigma E_0 e^{-(1+j)z/\delta_s} \right) \cdot \left( \hat{\bf x}~dy~dz \right) \nonumber \\ &= \sigma E_0 W \int_{z=0}^{\infty} e^{-(1+j)z/\delta_s} dz \label{m0159_eI}\end{align} \]
Para mayor comodidad, definamos la constante\(K \triangleq (1+j)/\delta_s\). Dado que\(K\) es constante con respecto a\(z\), la integral restante es sencilla de evaluar:
\[\begin{align} \int_0^{\infty} e^{-Kz}dz &= \left. -\frac{1}{K} e^{-Kz}\right|_0^{\infty} \nonumber \\ &= +\frac{1}{K}\end{align} \nonumber \]
Incorporando este resultado en la Ecuación\ ref {M0159_EI}, obtenemos:
\[\widetilde{I} \approx \sigma E_0 W \frac{\delta_s}{1+j} %\label{m0159_eI} \]
Calculamos\(\widetilde{V}\) para una longitud\(l\) del cable de la siguiente manera:
\[\widetilde{V} = -\int_{x=l}^{0} \widetilde{\bf E}\cdot d{\bf l} \nonumber \]
donde hemos determinado que\(x=0\) corresponde al terminal “\(+\)” y\(x=l\) corresponde al terminal “\(-\)”. 2 El camino de integración puede ser cualquier camino que comience y termine en las terminales proscritas. El camino más simple a utilizar es uno a lo largo de la superficie, paralelo al\(x\) eje. A lo largo de este camino,\(z=0\) y así\(\widetilde{\bf E}=\hat{\bf x}E_0\). Para este camino:
\[\widetilde{V} = -\int_{x=l}^{0} \left(\hat{\bf x}E_0\right)\cdot \left(\hat{\bf x}dx\right) = E_0 l \label{m0159_eV} \]
La impedancia\(Z\) medida a través de los terminales en\(x=0\) y ahora\(x=l\) se determina que es:
\[Z \triangleq \frac{\widetilde{V}}{\widetilde{I}} \approx \frac{1+j}{\sigma\delta_s} \cdot \frac{l}{W} \label{m0159_eCFGC-Z} \]
La resistencia es simplemente la parte real, así que obtenemos
\[R \approx \frac{l}{\sigma(\delta_s W)} ~~~~\mbox{(AC case)} \label{m0159_eACZ} \]
La cantidad\(R\) en este caso es referida específicamente como la resistencia óhmica, ya que se debe enteramente a la conductividad limitada del material cuantificada por la ley de Ohm. 3
Observe el parecido con la Ecuación\ ref {M0159_ERW} (la solución para el caso DC): En el caso AC, el producto\(\delta_s W\), que tiene unidades de área, juega el papel de la sección transversal física\(S\). Así, vemos una nueva interpretación interesante de la profundidad de la piel\(\delta_s\): Es la profundidad a la que una corriente uniforme (CC) necesitaría fluir para producir una resistencia igual a la resistencia observada (AC).
Se obtuvieron las ecuaciones\ ref {M0159_ECFGC-Z} y\ ref {M0159_EACZ} para un buen conductor llenando un semiespacio infinito, teniendo una superficie plana. ¿Qué tan bien describen estos resultados un alambre cilíndrico? La respuesta depende del radio del cable,\(a\). Para\(\delta_s \ll a\), las Ecuaciones\ ref {M0159_ECFGC-Z} y\ ref {M0159_EACZ} son aproximaciones excelentes, ya que\(\delta_s \ll a\) implica que la mayor parte de la corriente se encuentra en una capa delgada cercana a la superficie del alambre. En este caso, el modelo utilizado para desarrollar las ecuaciones es una buena aproximación para cualquier corte radial dado a través del alambre, y estamos justificados en reemplazar\(W\) con la circunferencia\(2\pi a\). Así, obtenemos las siguientes expresiones:
\[\boxed{ Z \approx \frac{1+j}{\sigma\delta_s} \cdot \frac{l}{2\pi a} ~~~ (\delta_s \ll a) } \label{m0159_eZW} \]
y así
\[\boxed{ R \approx \frac{l}{\sigma(\delta_s 2\pi a)} ~~~ (\delta_s \ll a) } \label{m0159_eRWAC} \]
La impedancia de un cable de longitud\(l\) y radio\(a\gg\delta_s\) viene dada por la Ecuación\ ref {M0159_EZW}. La resistencia de tal alambre viene dada por la Ecuación\ ref {M0159_ERWAC}.
Si, por otro lado,\(a < \delta_s\) o simplemente\(\sim \delta_s\), entonces la densidad de corriente es significativa en todo el cable, incluso a lo largo del eje del cable. En este caso, no podemos suponer que la densidad de corriente decae suavemente a cero al aumentar la distancia desde la superficie, por lo que el modelo que conduce a la Ecuación\ ref {M0159_EZW} es una mala aproximación. La frecuencia requerida para la validez de la Ecuación\ ref {M0159_EZW} se puede determinar señalando que\(\delta_s \approx 1/\sqrt{\pi f \mu \sigma}\) para un buen conductor; por lo tanto, requerimos
\[\frac{1}{\sqrt{\pi f \mu \sigma}} \ll a \nonumber \]
para que las expresiones derivadas sean válidas. Resolviendo para\(f\), encontramos:
\[f \gg \frac{1}{\pi \mu \sigma a^2} \label{m0159_efvalid} \]
Para cables comúnmente encontrados compuestos por conductores buenos típicos, esta condición se aplica a frecuencias en el régimen de MHz y superiores.
Estos resultados nos llevan a un hallazgo interesante adicional sobre la resistencia de CA de los cables. Ya que\(\delta_s \approx 1/\sqrt{\pi f \mu\sigma}\) para un buen conductor, la Ecuación\ ref {M0159_ERWAC} puede ser reescrita en la siguiente forma:
\[\boxed{ R \approx \frac{1}{2} \sqrt{\frac{\mu f}{\pi \sigma}} \cdot \frac{l}{a} } \label{m0159_eACZ2} \]
Hemos encontrado que\(R\) es aproximadamente proporcional a\(\sqrt{f}\). Por ejemplo, aumentar la frecuencia en un factor de 4 aumenta la resistencia en un factor de 2. Esta dependencia de frecuencia es evidente en todo tipo de cables prácticos y líneas de transmisión. Resumiendo:
La resistencia de un cable compuesto por un conductor bueno pero imperfecto es proporcional a la raíz cuadrada de frecuencia.
En este punto, hemos determinado que la resistencia viene dada aproximadamente por la Ecuación\ ref {M0159_EACz2} para\(\delta_s \ll a\), correspondiente a frecuencias en el régimen de MHz y superiores, y por la Ecuación\ ref {M0159_ERW} para\(\delta_s \gg a\), típicamente correspondientes a frecuencias en el régimen de kHz y por debajo. También hemos encontrado que la resistencia cambia lentamente con la frecuencia; es decir, en proporción a\(\sqrt{f}\). Por lo tanto, a menudo es posible estimar aproximadamente la resistencia a frecuencias entre estos dos regímenes de frecuencia comparando la resistencia de CC de la Ecuación\ ref {M0159_ERW} con la resistencia de CA de la Ecuación\ ref {M0159_EACz2}. A continuación se muestra un ejemplo.
En otros lugares hemos considerado el cable coaxial RG-59 (ver la sección “Línea Coaxial”, que puede aparecer en otro volumen dependiendo de la versión de este libro). Señalamos que no fue posible determinar la resistencia de CA por unidad de longitud\(R'\) para RG-59 a partir de consideraciones puramente electrostáticas y magnetostáticas. Ahora podemos considerar la resistencia por unidad de longitud del conductor interno, que es un cable sólido del tipo considerado en esta sección. Vamos a referirnos a esta cantidad como\(R'_{ic}\). Tenga en cuenta que
\[R' = R'_{ic} + R'_{oc} \nonumber \]
donde\(R'_{oc}\) es la resistencia por unidad de longitud del conductor externo. \(R'_{oc}\)sigue siendo un poco complicado de abordar aquí. Sin embargo,\(R'_{ic}\) suele ser mucho mayor que\(R'_{oc}\), entonces\(R' \sim R'_{ic}\). Es decir, tenemos una idea bastante buena de\(R'\) para RG-59 al considerar solo el conductor interno.
Los parámetros relevantes del conductor interno son\(\mu\approx\mu_0\),\(\sigma\cong 2.28 \times 10^7\) S/m, y\(a\cong 0.292\) mm. Usando la ecuación\ ref {M0159_EACz2}, encontramos:
\[\begin{aligned} R'_{ic} &\triangleq \frac{R_{ic}}{l} = \frac{1}{2}\sqrt{\frac{\mu f}{\pi \sigma}} \cdot \frac{1}{a} \nonumber \\ &\cong \left(227~\mu\Omega\cdot\mbox{m}^{-1}\cdot\mbox{Hz}^{-1/2}\right) \sqrt{f} \end{aligned} \nonumber \]
Usando Expression\ ref {m0159_efvalid}, encontramos que esto es válido solo para\(f \gg 130\) kHz. Entonces, por ejemplo, podemos estar seguros de que\(R'_{ic} \approx 0.82~\Omega\) /m a 13 MHz.
En el otro extremo (\(f \ll 130\)kHz), la Ecuación\ ref {M0159_ERW} (la resistencia DC) es una mejor estimación. En este caso de baja frecuencia, estimamos que\(R'_{ic} \approx 0.16~\Omega\) /m y es aproximadamente constante con la frecuencia.
Ahora tenemos una imagen completa: A medida que la frecuencia se incrementa de CC a 13 MHz,\(R'_{ic}\) esperamos que aumente monótonamente de\(\approx 0.16~\Omega\) /m a\(\approx 0.82~\Omega\) /m, y continuará aumentando en proporción a\(\sqrt{f}\) partir de ese valor.
Volviendo a la Ecuación\ ref {M0159_ECFGC-Z}, vemos que la resistencia no es toda la historia aquí. La impedancia\(Z=R+jX\) también tiene un componente reactivo\(X\) igual a la resistencia\(R\); es decir,
\[X \approx R \approx \frac{l}{\sigma(\delta_s 2\pi a)} \nonumber \]
Esto es exclusivo de los buenos conductores a CA; es decir, no vemos tal reactancia en CC. Debido a que esta reactancia es positiva, a menudo se la denomina inductancia. Sin embargo, esto es engañoso ya que la inductancia se refiere a la capacidad de una estructura para almacenar energía en un campo magnético, y el almacenamiento de energía decididamente no es lo que está sucediendo aquí. La similitud con la inductancia es simplemente que esta reactancia es positiva, al igual que la reactancia asociada con la inductancia. Siempre y cuando tengamos esto en cuenta, es razonable modelar la reactancia del cable como una inductancia equivalente:
\[L_{eq} \approx \frac{1}{2\pi f} \cdot \frac{l}{\sigma(\delta_s 2\pi a)} \nonumber \]
Ahora sustituyendo una expresión por la profundidad de la piel:
\[\begin{align} L_{eq} &\approx \frac{1}{2\pi f} \cdot \sqrt{\frac{\pi f \mu}{\sigma}} \cdot \frac{l}{2\pi a} \nonumber \\ &= \frac{1}{4\pi^{3/2}} \sqrt{\frac{\mu}{\sigma f}} \cdot \frac{l}{a} \label{m0159_eLeq2}\end{align} \]
para un alambre que tiene una sección transversal circular con\(\delta_s\ll a\). La utilidad de esta descripción es que facilita el modelado de la reactancia de cable como inductancia en un circuito equivalente. Resumiendo:
Un cable práctico puede modelarse usando un circuito equivalente que consiste en una resistencia ideal (Ecuación\ ref {M0159_EACz2}) en serie con un inductor ideal (Ecuación\ ref {M0159_Eleq2}). Mientras que la resistencia aumenta con la raíz cuadrada de la frecuencia, la inductancia disminuye con la raíz cuadrada de la frecuencia.
Si la reactancia positiva de un cable no se debe a la inductancia física, entonces ¿a qué mecanismo físico debemos atribuir este efecto? Un cable tiene reactancia porque hay un desplazamiento de fase entre el potencial y la corriente. Esto es evidente al comparar la Ecuación\ ref {M0159_EI} con la Ecuación\ ref {M0159_eV}. Este es el mismo desplazamiento de fase que se encontró que existe entre los campos eléctrico y magnético que se propagan en un buen conductor, como se explica en la Sección 3.11.
En otra parte del libro se averiguó que la inductancia por unidad\(L'\) de longitud del cable coaxial RG-59 era de aproximadamente\(370\) NH/m, calculamos esto a partir de consideraciones magnetostáticas, por lo que la reactancia asociada al efecto de la piel no se incluye en esta estimación. Veamos cómo\(L'\) se ve afectado por el efecto piel para el conductor interno. Usando la Ecuación\ ref {M0159_EleQ2} con\(\mu=\mu_0\),\(\sigma\cong 2.28 \times 10^7\) S/m, y\(a\cong 0.292\) mm, encontramos
\[L_{eq} \approx \left( 3.61 \times 10^{-5}~\mbox{H$\cdot$m$^{-1}\cdot$Hz$^{1/2}$} \right) \frac{l}{\sqrt{f}} \nonumber \]
Longitud por unidad:
\[L_{eq}' \triangleq \frac{L_{eq}}{l} \approx \frac{3.61 \times 10^{-5}~\mbox{H$\cdot$Hz$^{1/2}$}}{\sqrt{f}} \nonumber \]
Esto equivale a la inductancia magnetostática por unidad de longitud (\(\approx 370\)NH/m) a\(f \approx 9.52\) kHz, y disminuye con el aumento de la frecuencia.
Resumiendo: La inductancia equivalente asociada al efecto piel es tan importante como la inductancia magnetostática en el régimen de kHz, y se vuelve poco a poco menos importante con el aumento de la frecuencia.
Recordemos que la velocidad de fase en una línea de transmisión de baja pérdida es aproximadamente\(1/\sqrt{L'C'}\). Esto significa que el efecto de la piel hace que la velocidad de fase en tales líneas disminuya con la frecuencia decreciente. En otras palabras:
El efecto cutáneo en los conductores que comprenden líneas de transmisión comunes conduce a una forma de dispersión en la que las frecuencias más altas viajan más rápido que las frecuencias más bajas.
Este fenómeno se conoce como dispersión cromática, o simplemente “dispersión”, y conduce a una distorsión significativa para señales que tienen grandes anchos de banda.
Lectura adicional:
- “Efecto piel” en Wikipedia.
- Para ser claros, esta es la “forma puntual” de la ley de Ohm, a diferencia de la forma de teoría de circuitos (\(V=IR\)). ↩
- Si esto no está claro, recordemos que el vector de campo eléctrico debe apuntar lejos de la carga positiva (así, el\(+\) terminal). ↩
- Esto contrasta con otras formas en que se pueden relacionar voltaje y corriente; por ejemplo, la\(I\) característica no lineal\(V\) de un diodo, que no se rige por la ley de Ohm. ↩