6.8: Guía de ondas rectangular - Modos TM

Una guía de ondas rectangular es un cilindro conductor de sección transversal rectangular utilizado para guiar la propagación de las ondas. La guía de onda rectangular se usa comúnmente para el transporte de señales de radiofrecuencia a frecuencias en la banda SHF (3—30 GHz) y superiores. Los campos en una guía de ondas rectangular consisten en una serie de modos de propagación que dependen de las dimensiones eléctricas de la guía de ondas. Estos modos se clasifican ampliamente como magnéticos transversales (TM) o eléctricos transversales (TE). En esta sección, consideramos los modos TM.

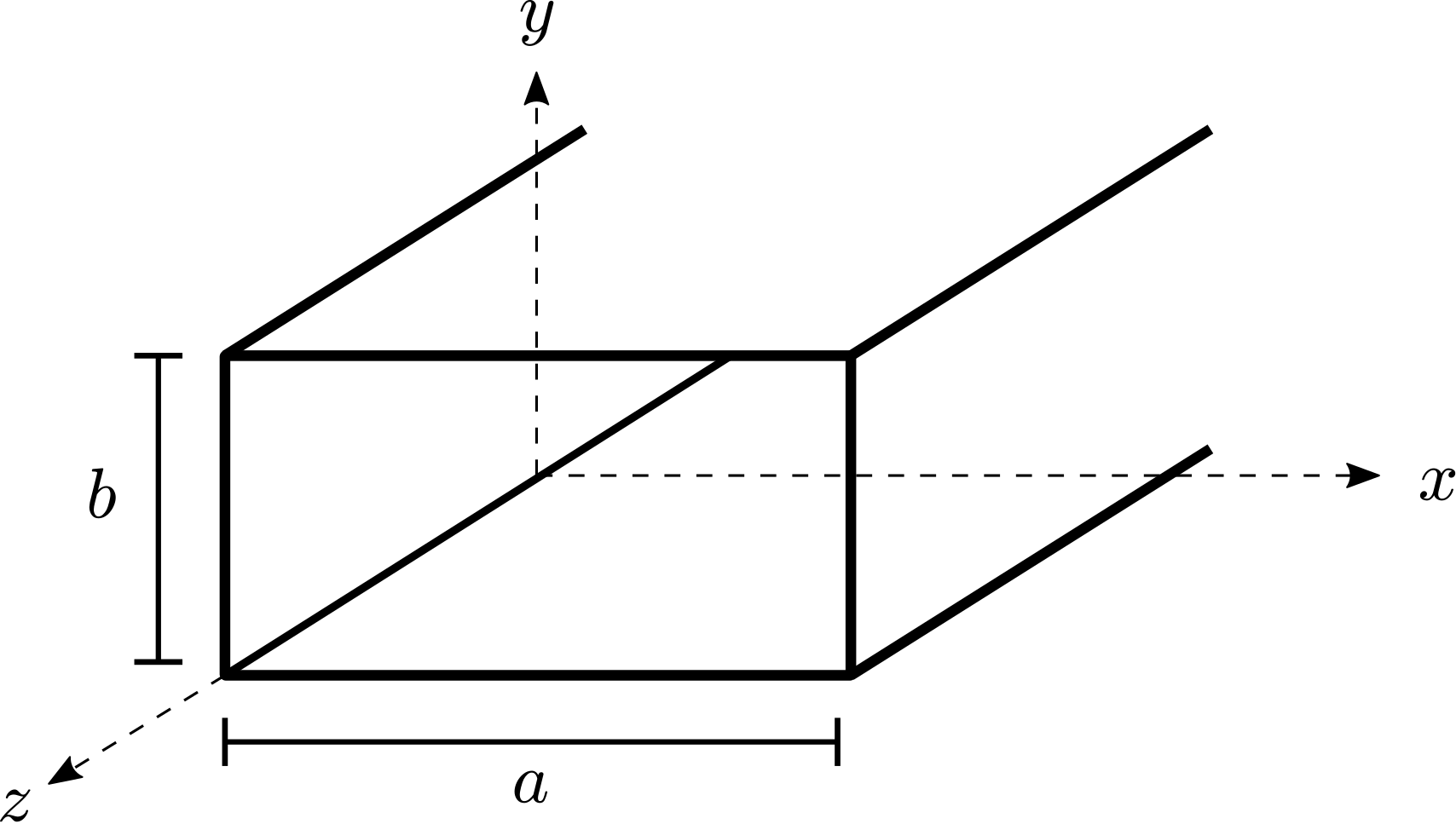
La figura$\PageIndex{1}$ muestra la geometría de interés. Aquí las paredes se encuentran en$x=0$,,$x=a$$y=0$, y$y=b$; así, las dimensiones de la sección transversal de la guía de ondas son$a$ y$b$. Se presume que el interior de la guía de ondas consiste en un material sin pérdidas que exhibe permeabilidad de valor real$\mu$ y permitividad de valor real$\epsilon$, y se supone que las paredes son perfectamente conductoras.

Figura$\PageIndex{1}$: Geometría para análisis de campos en una guía de ondas rectangular.

Limitemos nuestra atención a una región dentro de la guía de ondas que está libre de fuentes. Expresado en forma de fasor, la intensidad del campo eléctrico dentro de la guía de ondas se rige por la ecuación de onda

$$\nabla^2 \widetilde{\bf E} + \beta^2 \widetilde{\bf E} = 0 \label{m0223_eWE}$$

donde

$$\beta = \omega \sqrt{\mu \epsilon} \nonumber$$

La ecuación\ ref {M0223_EWE} es una ecuación diferencial parcial. Esta ecuación, combinada con las condiciones límite impuestas por las placas perfectamente conductoras, es suficiente para determinar una solución única. Esta solución se determina más fácilmente en coordenadas cartesianas, como ahora demostraremos. Primero expresamos$\widetilde{\bf E}$ en coordenadas cartesianas:

$$\widetilde{\bf E} = \hat{\bf x}\widetilde{E}_x + \hat{\bf y}\widetilde{E}_y + \hat{\bf z}\widetilde{E}_z \label{m0223_eE}$$

Esto facilita la descomposición de la Ecuación\ ref {M0223_EWE} en ecuaciones separadas que gobiernan los$\hat{\bf x}$$\hat{\bf y}$,, y$\hat{\bf z}$ componentes de$\widetilde{\bf E}$:

$$\begin{align} \nabla^2 \widetilde{E}_x + \beta^2 \widetilde{E}_x &= 0 \\ \nabla^2 \widetilde{E}_y + \beta^2 \widetilde{E}_y &= 0 \\ \nabla^2 \widetilde{E}_z + \beta^2 \widetilde{E}_z &= 0 \end{align} \nonumber$$

A continuación observamos que el operador$\nabla^2$ puede expresarse en coordenadas cartesianas de la siguiente manera:

$$\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \nonumber$$

por lo que las ecuaciones que rigen los componentes cartesianos de$\widetilde{\bf E}$ pueden escribirse de la siguiente manera:

\ begin {align}\ frac {\ parcial^2} {\ parcial x^2}\ Widetilde {E} _x +\ frac {\ parcial^2} {\ parcial y^2}\ Widetilde {E} _x +\ frac {\ parcial^2} {\ parcial z^2}\ Widetilde {E} _x +\ bettila^2\ ancho de {E} _x &= 0\ label {M0223_EEFx}\\ frac {\ parcial^2} {\ parcial x^2}\ tilde ancho {E} _y +\ frac {\ parcial^2} {\ parcial y^2}\ tilde ancha {E} _y + \ frac {\ parcial^2} {\ parcial z^2}\ Widetilde {E} _y +\ beta^2\ Widetilde {E} _y &= 0\ label {M0223_EEFy}\\ frac {\ parcial^2} {\ parcial x^2}\ Widetilde {E} _z +\ frac {\ al^2} {\ parcial y^2}\ Widetilde {E} _z +\ frac {\ parcial^2} {\ parcial z^2}\ Widetilde {E} _z +\ beta^2\ Widetilde {E} _z &= 0\ label {M0223_EEFZ}\ end {align}

En general, esperamos que el campo total en la guía de ondas consista en ondas unidireccionales que se propagan en las$-\hat{\bf z}$ direcciones$+\hat{\bf z}$ y. Podemos analizar cualquiera de estas ondas; entonces la otra onda se deriva fácilmente a través de la simetría, y el campo total es simplemente una combinación lineal (superposición) de estas ondas. Con esto en mente, limitamos nuestro enfoque a la onda que se propaga en la$+\hat{\bf z}$ dirección.

En la Sección 6.7, se muestra que todos los componentes de los campos eléctrico y magnético pueden calcularse fácilmente una vez$\widetilde{E}_z$ y$\widetilde{H}_z$ son conocidos. El problema se simplifica aún más al descomponer la onda unidireccional en componentes TM y TE. En esta descomposición, el componente TM se define por la propiedad que$\widetilde{H}_z=0$; es decir, es transversal (perpendicular) a la dirección de propagación. Así, el componente TM está completamente determinado por$\widetilde{E}_z$. Las ecuaciones 6.7.21 - 6.7.24 simplifican para convertirse en:

\ begin {align}\ Widetilde {E} _x &= -j\ frac {k_z} {k_ {\ rho} ^2}\ frac {\ parcial\ Widetilde {E} _z} {\ parcial x}\ etiqueta {M0223_Eexu}\\\ tilde ancha {E} _y &= -j\ frac {k_z} {k_z} _ {\ rho} ^2}\ frac {\ parcial\ Widetilde {E} _z} {\ parcial y}\ etiqueta {M0223_Eeyu}\\\ tilde ancho {H} _x &= +j\ frac {\ omega\ mu} {k_ {\ rho} ^2}\ frac {\ parcial\ Widetilde {E} _z} {\ parcial y}\ etiqueta {M0223_eHXU}\\\ Widetilde {H} _y &= -j\ frac {\ omega\ mu} {k_ {\ rho} ^2}\ frac {\ parcial\ Widetilde {E} _z} {\ parcial x}\ etiqueta {M0223_ehyu}\ final alinear}

donde

$$k_{\rho}^2 \triangleq \beta^2 - k_z^2 \label{m0223_ekrho}$$

y$k_z$ es la constante de propagación de fase; es decir, se supone que la onda se propaga de acuerdo con$e^{-jk_z z}$.

Ahora abordemos el problema del hallazgo$\widetilde{E}_z$, que luego determinará completamente el campo TM. Al igual que en la Sección 6.7, reconocemos que se$\widetilde{E}_z$ puede representar como el factor$e^{-jk_z z}$ de propagación multiplicado por un factor que describe la variación con respecto a las dimensiones espaciales restantes$x$ y$y$:

$$\widetilde{E}_z = \widetilde{e}_z(x,y) e^{-jk_z z} \nonumber$$

Sustitución de esta expresión en Ecuación\ ref {M0223_EEFz} y dividiendo el factor común de$e^{-jk_z z}$ rendimientos:

$$\frac{\partial^2}{\partial x^2}\widetilde{e}_z + \frac{\partial^2}{\partial y^2}\widetilde{e}_z - k_z^2 \widetilde{e}_z + \beta^2 \widetilde{e}_z = 0 \nonumber$$

Los dos últimos términos se pueden combinar usando la ecuación\ ref {m0223_ekrho}, dando:

$$\frac{\partial^2}{\partial x^2}\widetilde{e}_z + \frac{\partial^2}{\partial y^2}\widetilde{e}_z + k_{\rho}^2 \widetilde{e}_z = 0 \label{m0223_eDE1}$$

Esta es una ecuación diferencial parcial para$\widetilde{e}_z$ en las variables$x$ y$y$. Esta ecuación puede resolverse utilizando la técnica de separación de variables. En esta técnica, reconocemos que se$\widetilde{e}_z(x,y)$ puede escribir como el producto de una función de la$X(x)$ que depende solamente$x$, y una función de la$Y(y)$ que depende únicamente$y$. Es decir,

$$\widetilde{e}_z(x,y) = X(x) Y(y) \nonumber$$

Sustituyendo esta expresión en la Ecuación\ ref {M0223_Ede1}, obtenemos:

$$Y\frac{\partial^2}{\partial x^2}X + X\frac{\partial^2}{\partial y^2}Y + k_{\rho}^2 XY = 0 \label{m0223_eDE2}$$

A continuación dividiendo por$XY$, obtenemos:

$$\frac{1}{X}\frac{\partial^2}{\partial x^2}X + \frac{1}{Y}\frac{\partial^2}{\partial y^2}Y + k_{\rho}^2 = 0 \label{m0223_eDE3}$$

Obsérvese que el primer término depende sólo de$x$, el segundo término depende únicamente de$y$, y el término restante es una constante. Por lo tanto, la suma de los términos primero y segundo es una constante; a saber$-k_{\rho}^2$. Dado que estos términos dependen de uno$x$ o$y$, y no de ambos, el primer término debe ser igual a alguna constante, el segundo término debe ser igual a alguna constante, y estas constantes deben sumar a$-k_{\rho}^2$. Por lo tanto, estamos justificados al separar la ecuación en dos ecuaciones de la siguiente manera:

\ begin {align}\ frac {1} {X}\ frac {\ parcial^2} {\ parcial x^2} X + k_x^2 &= 0\ label {M0223_Ede4x}\\ frac {1} {Y}\ frac {\ parcial^2} {\ parcial y^2} Y + k_y^2 &= 0\ etiqueta {M0223_Ede4y}\ end {align}

donde las nuevas constantes$k_x^2$ y$k_y^2$ deben satisfacer

$$k_x^2+k_y^2 = k_{\rho}^2 \nonumber$$

Ahora multiplicando las Ecuaciones\ ref {M0223_Ede4X} y\ ref {$X$M0223_Ede4y} por y$Y$, respectivamente, encontramos:

\ begin {align}\ frac {\ parcial^2} {\ parcial x^2} X + k_x^2 X &= 0\ label {M0223_ede5x}\\ frac {\ parcial^2} {\ parcial y^2} Y + k_y^2 Y &= 0\ etiqueta {M0223_Ede5y}\ end {align}

Se trata de ecuaciones diferenciales unidimensionales familiares. Las soluciones son: ¹

\ begin {align} X &= A\ cos\ izquierda (k_x x\ derecha) + B\ sin\ izquierda (k_x x\ derecha)\ label {M0223_ex}\\ Y &= C\ cos\ izquierda (k_y y\ derecha) + D\ sin\ izquierda (k_y y\ derecha)\ etiqueta {M0223_ey}\ end {align}

donde$A$,$B$,$C$, y$D$ — como$k_x$ y$k_y$ — son constantes por determinar. En este punto, observamos que la ola que buscamos se puede expresar de la siguiente manera:

\ begin {align}\ Widetilde {E} _z &=\ Widetilde {e} _z (x, y) e^ {-jk_z z}\ nonumber\\ &= X (x) ~Y (y) ~e^ {-jk_z z}\ label {M0223_EezXYZ}\ end {align}

La solución es esencialmente completa a excepción de los valores de las constantes$A$$B$,$C$,$D$,$k_x$, y$k_y$. Los valores de estas constantes se determinan aplicando la condición de límite electromagnético relevante. En este caso, se requiere que el componente de$\widetilde{\bf E}$ eso es tangente a una pared perfectamente conductora debe ser cero. Tenga en cuenta que el$\hat{\bf z}$ componente de$\widetilde{\bf E}$ es tangente a las cuatro paredes; por lo tanto:

\ begin {align}\ Widetilde {E} _z\ izquierda (x=0\ derecha) &= 0\\\ Widetilde {E} _z\ izquierda (x=a\ derecha) &= 0\\ Widetilde {E} _z\ izquierda (y=0\ derecha) &= 0\\\ Widetilde {E} _z\ izquierda (y=b\ derecha) &= 0\ end {align}

Haciendo referencia a la Ecuación\ ref {M0223_EezXYZ}, estas condiciones de límite a su vez requieren:

\ begin {align} X\ left (x=0\ right) &= 0\\ X\ left (x=a\ right) &= 0\\ Y\ left (y=0\ right) &= 0\\ Y\ left (y=b\ right) &= 0\ end {align}

Evaluar estas condiciones usando Ecuaciones\ ref {M0223_ex} y\ ref {M0223_ey} rinde:

\ begin {align} A\ cdot 1 + B\ cdot 0 &= 0\ label {m0223_exbc1}\\ A\ cos\ izquierda (k_x a\ derecha) + B\ sin\ izquierda (k_x a\ derecha) &= 0\ label {m0223_exbc2}\\ C\ cdot 1 + D\ cdot 0 &= 0\ label {m0223_EYBC1}\\ C\ cos\ izquierda (k_y b\ derecha) + D\ sin\ izquierda (k_y b\ derecha) &= 0\ etiqueta {M0223_EYBC2}\ end {align}

Las ecuaciones\ ref {M0223_ExBC1} y\ ref {M0223_EYBC1} se pueden satisfacer sólo si$A=0$ y$C=0$, respectivamente. Posteriormente, las Ecuaciones\ ref {M0223_ExBC2} y\ ref {M0223_EYBC2} reducen a:

\ begin {align}\ sin\ left (k_x a\ right) &= 0\ label {M0223_Exbc2a}\\\ sin\ izquierda (k_y b\ derecha) &= 0\ label {M0223_EYBC2a}\ end {align}

Esto a su vez requiere:

\ begin {align} k_x &=\ frac {m\ pi} {a} ~, ~~~ m=0, 1, 2... \ label {m0223_ekxm}\\ k_y &=\ frac {n\ pi} {b} ~, ~~~ n=0, 1, 2... \ label {m0223_ekyn}\ end {align}

Cada valor entero positivo de$m$ y$n$ conduce a una expresión válida para$\widetilde{E}_z$ conocido como modo. Soluciones para las cuales$m=0$ o$n=0$ rendimiento$k_x=0$ o$k_y=0$, respectivamente. Estos corresponden a campos de valor cero, y por lo tanto no son de interés. La expresión más general para$\widetilde{E}_z$ debe dar cuenta de todos los modos no triviales. Resumiendo:

$$\widetilde{E}_z = \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} \widetilde{E}_z^{(m,n)} \label{m0223_eEzTMall}$$

donde

$$\widetilde{E}_z^{(m,n)} \triangleq E_0^{(m,n)} \sin\left(\frac{m\pi}{a} x\right) \sin\left(\frac{n\pi}{b} y\right) e^{-jk_z^{(m,n)} z} \label{m0223_eEzTM}$$

donde$E_0^{(m,n)}$ es una constante arbitraria (consolidando las constantes$B$ y$D$), y, desde$k_x^2 + k_y^2 = k_{\rho}^2 \triangleq \beta^2-k_z^2$:

$$k_z^{(m,n)} = \sqrt{ \omega^2\mu\epsilon - \left(\frac{m\pi}{a}\right)^2 - \left(\frac{n\pi}{b}\right)^2 } \label{m0223_ekzm}$$

Resumiendo:

El componente TM ($\widetilde{H}_z=0$) de la onda unidireccional ($+\hat{\bf z}$-viajera) en una guía de ondas rectangular está completamente determinado por la Ecuación\ ref {M0223_EeztMall}, y consiste en los modos definidos por las Ecuaciones\ ref {M0223_EEZTM},\ ref {m0223_ekzm},\ ref {m0223_ekxm}, y\ ref {m0223_ekyn}. Los componentes restantes de campo distintos de cero se pueden determinar usando Ecuaciones\ ref {M0223_EEXU} -\ ref {M0223_Ehyu}.

Es habitual y conveniente referirse a los modos TM en una guía de ondas rectangular usando la notación “TM”$_{mn}$. Por ejemplo, el modo TM$_{12}$ viene dado por la Ecuación\ ref {M0223_EEZTM} con$m=1$ y$n=2$.

Finalmente, tenga en cuenta que los valores de$k_z^{(m,n)}$ obtenidos de la Ecuación\ ref {m0223_ekzm} no son necesariamente de valor real. Es evidente que para cualquier valor dado de$m$,$k_z^{(m,n)}$ será imaginario-valorado para todos los valores de$n$ mayor que algún valor. De igual manera, es evidente que para cualquier valor dado de$n$,$k_z^{(m,n)}$ será imaginario-valorado para todos los valores de$m$ mayor que algún valor. Este fenómeno es común a los componentes de TM y TE, por lo que se aborda en una sección separada (Sección 6.10).

Lectura adicional:

• “Guía de ondas (radiofrecuencia)” en Wikipedia.
• “Separación de variables” en Wikipedia.

---

1. Se anima a los estudiantes a confirmar que estos son correctos al confirmar que son soluciones a las Ecuaciones\ ref {M0223_Ede5x} y\ ref {M0223_Ede5x}, respectivamente. ↩