8.3: Dispersión en Fibra Óptica

La luz puede seguir una variedad de caminos a través de un cable de fibra óptica. Cada uno de los caminos tiene una longitud diferente, lo que lleva a un fenómeno conocido como dispersión. La dispersión distorsiona las señales y limita la velocidad de datos de las señales digitales enviadas por cable de fibra óptica. En esta sección, analizamos esta dispersión y su efecto sobre las señales digitales.

La figura\(\PageIndex{1}\) muestra la variedad de caminos que la luz puede tomar a través de un cable de fibra óptica recto.

Figura\(\PageIndex{1}\): Trayectorias que la luz puede tomar a través de un cable de fibra óptica recto: (a) A lo largo del eje, correspondiente a la longitud mínima de la trayectoria; (b) Intermedio entre (a) y (c); (c) Longitud máxima, correspondiente al ángulo umbral para la reflexión interna total. (CC BY-SA 4.0; S. Lally)

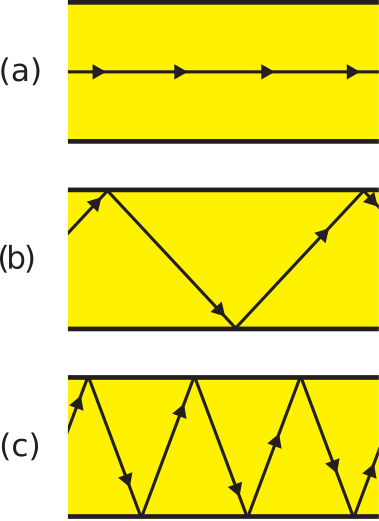
La trayectoria nominal se muestra en la Figura\(\PageIndex{1}\) (a), la cual es paralela al eje del cable. Esta ruta tiene el menor tiempo de propagación asociado. La ruta con el tiempo de propagación asociado más largo se muestra en la Figura\(\PageIndex{1}\) (c). En este caso, la luz rebota dentro de la fibra, cada vez que se acerca a la interfaz núcleo-revestida en el ángulo crítico para una reflexión interna total. Cualquier rayo que se aproxime a un ángulo mayor no se refleja completamente, por lo que probablemente no sobreviviría hasta el final del cable. La figura\(\PageIndex{1}\) (b) representa el continuo de posibilidades entre los casos extremos de (a) y (c), con tiempos de propagación asociados mayores que los del caso (a) pero menores que los del caso (c).

Independientemente de cómo se inserte la luz en la fibra, es probable que\(\PageIndex{1}\) existan todos los caminos posibles representados en la Figura. Esto se debe a que la fibra rara vez se instala en línea recta, sino que sigue un camino de múltiples curvas. Cada curva da como resultado nuevos ángulos de incidencia sobre el límite núcleo-revestimiento. La existencia de estos caminos conduce a la dispersión. Para ver esto, considere la señal de entrada que se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Una señal digital que podría aplicarse a la entrada de un cable de fibra óptica. (CC BY-SA 4.0; S. Lally)

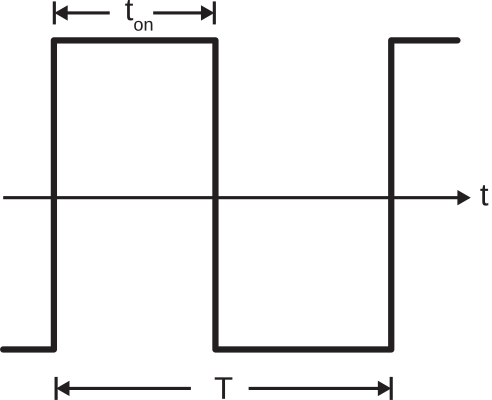
Esta señal tiene periodo\(T\), tiempo durante el cual\(t_{on}<T\) puede estar presente un pulso de longitud. Dejar que sea el tiempo mínimo de propagación a través de la fibra (como en la Figura\(\PageIndex{1}\) (a))\(\tau_{min}\). Dejar que sea el tiempo máximo de propagación a través de la fibra (como en la Figura\(\PageIndex{1}\) (c))\(\tau_{max}\). Si\(\tau_{max}-\tau_{min}\ll t_{on}\), vemos poca degradación en la salida de señal de la fibra. De lo contrario, observamos una “mancha” de pulsos en la salida de la fibra, como se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): El efecto de la dispersión en la salida de señal del cable de fibra óptica: Arriba: Forma de onda de llegada correspondiente a la longitud mínima de trayectoria, Medio: Forma de onda de llegada correspondiente a la longitud máxima de trayectoria, e Inferior: Suma de todas las formas de onda que llegan. (CC BY-SA 4.0; S. Lally)

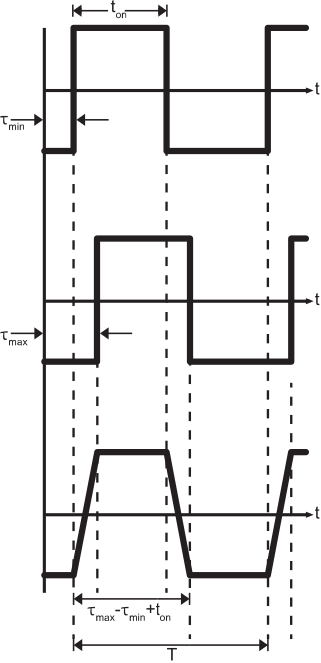
Cualquier mancha puede plantear problemas para cualquier dispositivo que esté detectando pulsos en el extremo receptor. Sin embargo, a medida que\(\tau_{max}-\tau_{min}\) se convierte en una fracción mayor de\(t_{on}\), vemos que es posible que los pulsos adyacentes se superpongan. Esto presenta un desafío mucho más serio en la detección de pulsos individuales, por lo que examinemos el problema de la superposición con mayor detalle. Para evitar superposiciones:

\[\tau_{max}-\tau_{min} + t_{on} < T \nonumber \]

Definamos la cantidad\(\tau \triangleq \tau_{max}-\tau_{min}\). Esto a veces se conoce como la propagación del retraso. ¹ Por lo tanto, obtenemos el siguiente requisito para la transmisión sin solapamiento:

\[\tau < T - t_{on} \nonumber \]

Tenga en cuenta que la propagación de retardo impone un valor mínimo\(T\), lo que a su vez impone un valor máximo a la velocidad a la que se puede transmitir información en el cable. Entonces, estamos motivados para calcular el diferencial de retraso. El tiempo mínimo de propagación\(t_{min}\) es simplemente la longitud\(l\) del cable dividido por la velocidad\(v_p\) de fase de la luz dentro del núcleo; es decir,\(t_{min} = l/v_p\). La velocidad de la fase de recuperación es simplemente la velocidad de la luz en el espacio libre\(c\) dividida por\(\sqrt{\epsilon_r}\) dónde\(\epsilon_r\) está la permitividad relativa del material del núcleo. Así:

\[t_{min} = \frac{l}{v_p} = \frac{l}{c/\sqrt{\epsilon_r}} = \frac{l}{c/n_f} = \frac{l n_f}{c} \nonumber \]

El tiempo máximo de propagación\(t_{max}\) es diferente porque la longitud máxima de la ruta es diferente. Específicamente, la longitud máxima de la trayectoria no es\(l\), sino más bien\(l/\cos\theta_2\) dónde\(\theta_2\) está el ángulo entre el eje y la dirección de desplazamiento a medida que la luz cruza el eje. Entonces, por\(\theta_2=0\) ejemplo,\(t_{min}\) ya que la luz en ese caso viaja a lo largo del eje. El valor de\(\theta_2\) for\(t_{max}\) está determinado por el ángulo umbral para la reflexión interna total. Esto se determinó en la Sección 8.2 a ser dado por:

\[\cos\theta_2 = \frac{n_c}{n_f} ~~~~~~\mbox{(threshold value)} \nonumber \]

por lo que obtenemos la siguiente relación:

\[t_{max} = \frac{l/\cos\theta_2}{v_p} = \frac{l n_f/n_c}{c/n_f} = \frac{l n_f^2}{c n_c} \nonumber \]

y posteriormente encontramos:

\[\boxed{ \tau = l \frac{n_f}{c} \left( \frac{n_f}{n_c} - 1 \right) } \label{m0193_eDS} \]

Tenga en cuenta que\(\tau\) aumenta linealmente con\(l\). Por lo tanto, la velocidad a la que los pulsos pueden enviarse sin solapamiento disminuye linealmente al aumentar la longitud. En aplicaciones prácticas, esto significa que la velocidad máxima de datos soportable disminuye a medida que aumenta la longitud del cable. Esto es cierto independientemente de la pérdida de medios dentro del cable (¡que aún no hemos considerado!). Más bien, esta es una limitación fundamental resultante de la dispersión.

Ejemplo\(\PageIndex{1}\): Maximum supportable data rate in multimode fiber optic cable

Se utiliza un cable de fibra óptica multimodo de 1 m de longitud para transmitir datos utilizando el esquema mostrado en la Figura\(\PageIndex{2}\), con\(t_{on}=T/2\). Los valores de\(n_f\) y\(n_c\) para esta fibra son 1.52 y 1.49, respectivamente. ¿Cuál es la velocidad máxima de datos soportable?

Solución

Usando la ecuación\ ref {M0193_EDS}, encontramos el retardo spread\(\tau\cong 102\) ps. Para evitar superposiciones,\(T>2\tau\); por lo tanto, se requiere\(T\) mayor a aproximadamente 204 ps. El esquema de modulación permite un bit por periodo, por lo que la velocidad máxima de datos es\(1/T\cong 4.9\times 10^9\) bits por segundo; es decir,\(\cong\) 4.9 Gb/s.

El hallazgo de 4.9 Gb/s puede parecer una velocidad de datos bastante alta; sin embargo, considere lo que sucede si la longitud aumenta a 1 km. Es evidente a partir de la Ecuación\ ref {M0193_EDS} que la propagación del retardo aumentará en un factor de 1000, por lo que la velocidad de datos máxima soportable disminuye en un factor de 1000 a un escaso 4.9 Mb/s. Nuevamente, esto es independiente de cualquier pérdida de medios dentro de la fibra. Para restaurar la mayor velocidad de datos a lo largo de esta ruta más larga, se debe reducir la dispersión. Una forma de hacerlo es dividir el enlace en enlaces más pequeños separados por repetidores que pueden recibir la señal dispersa, demodularla, regenerar la señal original y transmitir la señal restaurada al siguiente repetidor. Alternativamente, se puede emplear fibra “monomodo”, que tiene intrínsecamente menos dispersión que la fibra multimodo presunta en nuestro análisis.

---

1. Divulgación completa: Hay muchas formas de definir la “propagación del retraso”, pero esta definición no es infrecuente y es útil en el presente análisis. ↩