4.3: Convolución de Tiempo Discreta
- Page ID
- 86238
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
La convolución, uno de los conceptos más importantes en ingeniería eléctrica, se puede utilizar para determinar la salida que produce un sistema para una señal de entrada dada. Se puede demostrar que un sistema lineal invariante en el tiempo se caracteriza completamente por su respuesta impulsiva. La propiedad de tamizado de la función de impulso de tiempo discreto nos dice que la señal de entrada a un sistema puede representarse como una suma de impulsos unitarios escalados y desplazados. Así, por linealidad, parecería razonable calcular la señal de salida como la suma de respuestas de impulso de unidad escaladas y desplazadas. Eso es exactamente lo que logra la operación de convolución. Por lo tanto, la convolución se puede utilizar para determinar la salida de un sistema lineal invariante en el tiempo a partir del conocimiento de la entrada y la respuesta al impulso.
Convolución y Convolución Circular
Convolución
Definición de Operación
La convolución de tiempo discreta es una operación en dos señales de tiempo discretas definidas por la integral
\[(f * g)[n]=\sum_{k=-\infty}^{\infty} f[k] g[n-k] \nonumber \]
para todas las señales\(f\),\(g\) definido en\(\mathbb{Z}\). Es importante señalar que la operación de convolución es conmutativa, es decir, que
\[f * g=g * f \nonumber \]
para todas las señales\(f\),\(g\) definido en\(\mathbb{Z}\). Así, la operación de convolución podría haberse expresado con la misma facilidad usando la definición equivalente
\[(f * g)[n]=\sum_{k=-\infty}^{\infty} f[n-k] g[k] \nonumber \]
para todas las señales\(f\),\(g\) definido en\(\mathbb{Z}\). La convolución tiene varias otras propiedades importantes no enumeradas aquí pero explicadas y derivadas en un módulo posterior.
Definición Motivación
La definición de operación anterior ha sido elegida para ser particularmente útil en el estudio de sistemas lineales invariantes en el tiempo. Para ver esto, considere un sistema lineal invariante en el tiempo\(H\) con respuesta de impulso unitario\(h\). Dada una señal de entrada del sistema,\(x\) nos gustaría calcular la señal de salida del sistema\(H(x)\). Primero, observamos que la entrada se puede expresar como la convolución
\[x[n]=\sum_{k=-\infty}^{\infty} x[k] \delta[n-k] \nonumber \]
por la propiedad de tamizado de la función de impulso unitario. Por linealidad
\[ H(x[n])=\sum_{k=-\infty}^{\infty} x[k] H(\delta[n-k]). \nonumber \]
Dado que\(H(\delta[n-k])\) es la respuesta de impulso de la unidad desplazada\(h[n−k]\), esto da el resultado
\[ H(x[n])=\sum_{k=-\infty}^{\infty} x[k] h[n-k]=(x * h)[n]. \nonumber \]
De ahí que la convolución se haya definido de tal manera que la salida de un sistema lineal invariante en el tiempo viene dada por la convolución de la entrada del sistema con la respuesta de impulso de la unidad del sistema.
Intuición Gráfica
A menudo es útil poder visualizar el cálculo de una convolución en términos de procesos gráficos. Consideremos la convolución de dos funciones\(f\),\(g\) dadas por
\[(f * g)[n]=\sum_{k=-\infty}^{\infty} f[k] g[n-k]=\sum_{k=-\infty}^{\infty} f[n-k] g[k]. \nonumber \]
El primer paso para comprender gráficamente la operación de convolución es trazar cada una de las funciones. A continuación, se debe seleccionar una de las funciones, y su trazado se refleja a través del\(k=0\) eje. Para cada real\(n\), esa misma función debe ser desplazada a la izquierda por\(n\). Luego se calcula el producto puntual de las dos gráficas resultantes y luego se suman todos los valores.
Ejemplo\(\PageIndex{1}\)
Recuerde que la respuesta de impulso para un sistema de retroalimentación de eco de tiempo discreto con ganancia\(a\) es
\[h[n]=a^{n} u[n], \nonumber \]
y considerar la respuesta a una señal de entrada que es otra exponencial
\[x[n]=b^{n} u[n] . \nonumber \]
Sabemos que la salida para esta entrada viene dada por la convolución de la respuesta de impulso con la señal de entrada
\[y[n]=x[n] * h[n]. \nonumber \]
Nos gustaría computar esta operación comenzando de una manera que minimice la complejidad algebraica de la expresión. Sin embargo, en este caso, cada elección posible es igualmente sencilla. Así, nos gustaría calcular
\[ y[n]=\sum_{k=-\infty}^{\infty} a^{k} u[k] b^{n-k} u[n-k]. \nonumber \]
Las funciones de paso se pueden utilizar para simplificar aún más esta suma. Por lo tanto,
\[y[n]=0 \nonumber \]
para\(n<0\) y
\[y[n]=\sum_{k=0}^{n}[a b]^{k} \nonumber \]
para\(n \geq 0\). De ahí\(a b \neq 1\), siempre, tenemos que
\ [y [n] =\ izquierda\ {\ begin {array} {cc}
0 & n<0\\
\ frac {1- (a b) ^ {n+1}} {1- (a b)} & n\ geq 0
\ end {array}\ derecha. \ nonumber\]
Convolución Circular
La convolución circular de tiempo discreta es una operación en dos señales de tiempo discretas periódicas o de longitud finita definidas por la suma
\[(f \circledast g)[n]=\sum_{k=0}^{N-1} \hat{f}[k] \hat{g}[n-k] \nonumber \]
para todas las señales\(f\),\(g\) definidas en\(\mathbb{Z}[0, N-1]\) donde\(\hat{f}\),\(\hat{g}\) son extensiones periódicas de\(f\) y\(g\). Es importante señalar que la operación de convolución circular es conmutativa, es decir, que
\[f \circledast g = g \circledast f \nonumber \]
para todas las señales\(f\),\(g\) definido en\(\mathbb{Z}[0, N-1]\). Así, la operación de convolución circular podría haberse expresado con la misma facilidad usando la definición equivalente
\[(f \circledast g)[n]=\sum_{k=0}^{N-1} \hat{f}[n-k] \hat{g}[k] \nonumber \]
para todas las señales\(f\),\(g\) definidas en\(\mathbb{Z}[0, N-1]\) donde\(\hat{f}\),\(\hat{g}\) son extensiones periódicas de\(f\) y\(g\). La convolución circular tiene varias otras propiedades importantes no enumeradas aquí pero explicadas y derivadas en un módulo posterior.
Alternativamente, la convolución circular de tiempo discreta se puede expresar como la suma de dos sumas dadas por
\[(f \circledast g)[n]=\sum_{k=0}^{n} f[k] g[n-k]+\sum_{k=n+1}^{N-1} f[k] g[n-k+N] \nonumber \]
para todas las señales\(f\),\(g\) definido en\(\mathbb{Z}[0, N-1]\).
Ejemplos significativos de computación de circunvoluciones circulares de tiempo discretas en el dominio del tiempo implicarían manipulaciones algebraicas complicadas que se ocupan del comportamiento envolvente, lo que en última instancia sería más confuso que útil. Por lo tanto, ninguno se proporcionará en esta sección. Por supuesto, los cálculos de ejemplo en el dominio del tiempo son fáciles de programar y demostrar. Sin embargo, las circunvoluciones circulares de tiempo discretas se calculan más fácilmente usando herramientas de dominio de frecuencia como se mostrará en la sección de series discretas de Fourier de tiempo.
Definición Motivación
La definición de operación anterior ha sido elegida para ser particularmente útil en el estudio de sistemas lineales invariantes en el tiempo. Para ver esto, considere un sistema lineal invariante en el tiempo\(H\) con respuesta de impulso unitario\(h\). Dada una señal de entrada periódica del sistema,\(x\) nos gustaría calcular la señal de salida del sistema\(H(x)\). Primero, observamos que la entrada se puede expresar como la convolución circular
\[x[n]=\sum_{k=0}^{N-1} \widehat{x}[k] \hat{\delta}[n-k] \nonumber \]
por la propiedad de tamizado de la función de impulso unitario. Por linealidad,
\[H(x[n])=\sum_{k=0}^{N-1} \widehat{x}[k] H(\hat{\delta}[n-k]). \nonumber \]
Dado que\(H(\delta[n-k])\) es la respuesta de impulso de la unidad desplazada\(h[n−k]\), esto da el resultado
\[ H(x[n])=\sum_{k=0}^{N-1} \hat{x}[k] \hat{h}[n-k]=(x \circledast h)[n]. \nonumber \]
De ahí que la convolución circular se haya definido de tal manera que la salida de un sistema lineal invariante en el tiempo viene dada por la convolución de la entrada del sistema con la respuesta de impulso de la unidad del sistema.
Intuición Gráfica
A menudo es útil poder visualizar el cálculo de una convolución circular en términos de procesos gráficos. Considere la convolución circular de dos funciones de longitud finita\(f\),\(g\) dadas por
\[(f \circledast g)[n]=\sum_{k=0}^{N-1} \hat{f}[k] \hat{g}[n-k]=\sum_{k=0}^{N-1} \hat{f}[n-k] \hat{g}[k] \nonumber \]
El primer paso para comprender gráficamente la operación de convolución es trazar cada una de las extensiones periódicas de las funciones. A continuación, se debe seleccionar una de las funciones, y su trazado se refleja a través del\(k=0\) eje. Para cada uno\(n \in \mathbb{Z}[0, N-1]\), esa misma función debe ser desplazada a la izquierda por\(n\). Luego se calcula el producto puntual de las dos gráficas resultantes, y finalmente se suman todos estos valores.
Elemento interactivo
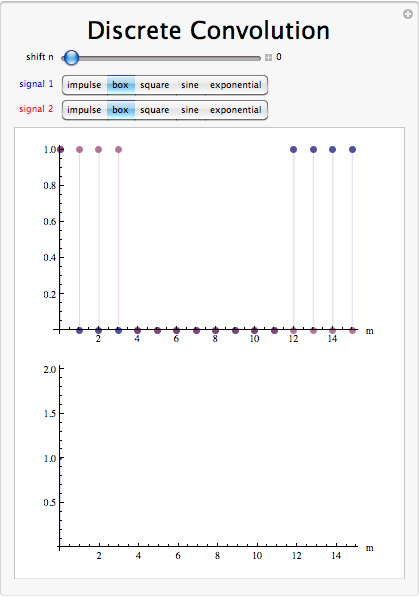
Resumen de convolución
La convolución, uno de los conceptos más importantes en ingeniería eléctrica, se puede utilizar para determinar la señal de salida de un sistema lineal invariable en el tiempo para una señal de entrada dada con conocimiento de la respuesta de impulso unitario del sistema. La operación de convolución de tiempo discreta se define de tal manera que realiza esta función para señales y sistemas de tiempo discretos de longitud infinita. La operación de convolución circular de tiempo discreta se define de tal manera que realiza esta función para señales de tiempo discretas periódicas y de longitud finita. En cada caso, la salida del sistema es la convolución o convolución circular de la señal de entrada con la respuesta de impulso de la unidad.


