6.7: Fenómenos de Gibbs

Introducción

La Serie de Fourier es la representación de señales periódicas de tiempo continuo en términos de exponenciales complejos. Las condiciones de Dirichlet sugieren que las señales discontinuas pueden tener una representación de la Serie de Fourier siempre que haya un número finito de discontinuidades. Esto parece contrario a la intuición, sin embargo, ya que los exponenciales complejos (Sección 1.8) son funciones continuas. No parece posible reconstruir exactamente una función discontinua a partir de un conjunto de continuas. De hecho, no lo es. No obstante, puede ser si relajamos la condición de 'exactamente' y la reemplazamos con la idea de 'casi en todas partes'. Es decir que la reconstrucción es exactamente la misma que la señal original excepto en un número finito de puntos. Estos puntos, no necesariamente de manera sorprendente, ocurren en los puntos de discontinuidades.

Historia

A finales del siglo XIX, se construyeron muchas máquinas para calcular los coeficientes de Fourier y volver a sintetizar:

\[f_{N}^{\prime}(t)=\sum_{n=-N}^{N} c_{n} e^{j \omega_{0} n t} \nonumber \]

Albert Michelson (un extraordinario físico experimental) construyó una máquina en 1898 que podía calcular\(c_n\) hasta\(n=\pm(79)\), y volvió a sintetizar

\[f_{79}^{\prime}(t)=\sum_{n=-79}^{79} c_{n} e^{j \omega_{0} n t} \nonumber \]

La máquina se desempeñó muy bien en todas las pruebas excepto en las que implicaban funciones discontinuas. Cuando una onda cuadrada, como la que se muestra en la Figura\(\PageIndex{1}\), fue ingresada en la máquina, aparecieron “meneo” alrededor de las discontinuidades, e incluso cuando el número de coeficientes de Fourier se acercaba al infinito, los meneo nunca desaparecieron, estos se pueden ver en la última gráfica de la Figura\(\PageIndex{1}\). J. Willard Gibbs explicó por primera vez este fenómeno en 1899, y por lo tanto a estos puntos discontinuos se les conoce como Fenómeno de Gibbs.

Explicación

Comenzamos esta discusión tomando una señal con un número finito de discontinuidades (como un pulso cuadrado) y encontrando su representación en la Serie de Fourier. Luego intentamos reconstruirlo a partir de estos coeficientes de Fourier. Lo que encontramos es que cuantos más coeficientes usemos, más comienza a parecerse la señal a la original. Sin embargo, alrededor de las discontinuidades, observamos ondulaciones que no parecen disminuir. Al considerar aún más coeficientes, notamos que las ondas se estrechan, pero no se acortan. A medida que nos acercamos a un número infinito de coeficientes, esta ondulación aún no desaparece. Es entonces cuando aplicamos la idea de casi todas partes. Si bien estas ondas permanecen (nunca cayendo por debajo del 9% de la altura del pulso), el área dentro de ellas tiende a cero, lo que significa que la energía de esta ondulación va a cero. Esto quiere decir que su ancho se acerca a cero y podemos afirmar que la reconstrucción es exactamente la original excepto en los puntos de discontinuidad. Dado que las condiciones de Dirichlet aseveran que sólo puede haber un número finito de discontinuidades, podemos concluir que se cumple el principio de casi todas partes. Este fenómeno es un caso específico de convergencia no uniforme.

A continuación utilizaremos la onda cuadrada, junto con su representación de la Serie de Fourier, y mostraremos varias figuras que revelan este fenómeno de manera más matemática.

Onda cuadrada

La representación en serie de Fourier de una señal cuadrada a continuación dice que los lados izquierdo y derecho son “iguales”. Para entender el Fenómeno Gibbs tendremos que redefinir la forma en que vemos la igualdad.

\[s(t)=a_{0}+\sum_{k=1}^{\infty} a_{k} \cos \left(\frac{2 \pi k t}{T}\right)+\sum_{k=1}^{\infty} b_{k} \sin \left(\frac{2 \pi k t}{T}\right) \nonumber \]

La figura\(\PageIndex{1}\) muestra varias aproximaciones de series de Fourier de la onda cuadrada usando un número variado de términos, denotados por KK:

Aproximaciones de series de Fourier de una onda cuadrada

Figura\(\PageIndex{1}\): Aproximación de la serie de Fourier a\(sq(t)\). El número de términos en la suma de Fourier se indica en cada gráfica, y la onda cuadrada se muestra como una línea discontinua en dos periodos.

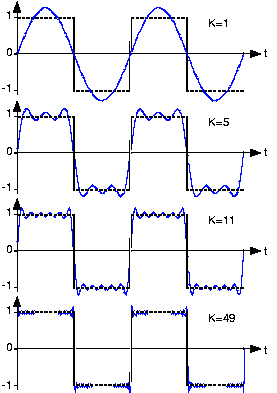
Al comparar la onda cuadrada con su representación en serie de Fourier en la Figura\(\PageIndex{1}\), no está claro que las dos sean iguales. El hecho de que la serie de Fourier de la onda cuadrada requiera más términos para una precisión de representación dada no es importante. Sin embargo, una inspección minuciosa de la Figura\(\PageIndex{1}\) revela un problema potencial: ¿La serie de Fourier realmente iguala a la onda cuadrada en todos los valores de tt? En particular, en cada cambio escalonado en la onda cuadrada, la serie de Fourier exhibe un pico seguido de oscilaciones rápidas. A medida que se agregan más términos a la serie, las oscilaciones parecen volverse más rápidas y más pequeñas, pero los picos no van disminuyendo. Considera esta pregunta matemática de manera intuitiva: ¿Puede una función discontinua, como la onda cuadrada, expresarse como una suma, incluso infinita, de continuas? Uno debe por lo menos sospechar, y de hecho, no se puede expresar así. Este número trajo a Fourier muchas críticas de la Academia Francesa de Ciencias (Laplace, Legendre y Lagrange comprendían el comité de revisión) durante varios años después de su presentación en 1807. No se resolvió por también un siglo, y su resolución es interesante e importante de entender desde un punto de vista práctico.

Los picos extraños en la serie de Fourier de la onda cuadrada nunca desaparecen; se les llama fenómeno de Gibb después del físico estadounidense Josiah Willard Gibbs. Se producen siempre que la señal es discontinua, y siempre estarán presentes siempre que la señal tenga saltos.

Redefinir la igualdad

Volvamos a la cuestión de la igualdad; ¿cómo puede justificarse el signo igual en la definición de la serie de Fourier (Sección 4.3)? La respuesta parcial es que no se garantiza puntualmente —todos y cada uno de los valores de\(t\) — la igualdad. Lo que los matemáticos más tarde en el siglo XIX mostraron fue que el error rms de la serie de Fourier siempre fue cero.

\[\lim_{K \rightarrow \infty} \operatorname{rms}\left(\varepsilon_{K}\right)=0 \nonumber \]

Lo que esto significa es que la diferencia entre una señal real y su representación en serie de Fourier puede no ser cero, ¡pero el cuadrado de esta cantidad tiene cero integral! Es a través de los ojos del valor rms que definimos la igualdad: Dos señales\(s_1(t)\),\(s_2(t)\) se dice que son iguales en el cuadrado medio si rms\((s_1−s_2)=0\). Se dice que estas señales son iguales puntualmente si\(s_1(t)=s_2(t)\) para todos los valores de\(t\). Para las series de Fourier, los picos del fenómeno de Gibb tienen altura finita y ancho cero: El error difiere de cero solo en puntos aislados, siempre que la señal periódica contenga discontinuidades, y equivale a aproximadamente 9% del tamaño de la discontinuidad. El valor de una función en un conjunto finito de puntos no afecta su integral. Este efecto subyace a la razón por la que definir el valor de una función discontinua en su discontinuidad no tiene sentido. Cualquier cosa que elija para un valor no tiene relevancia práctica ni para el espectro de la señal ni para la forma en que un sistema responde a la señal. El valor de la serie de Fourier “a” la discontinuidad es el promedio de los valores a cada lado del salto.

Visualizando los Fenómenos de Gibb

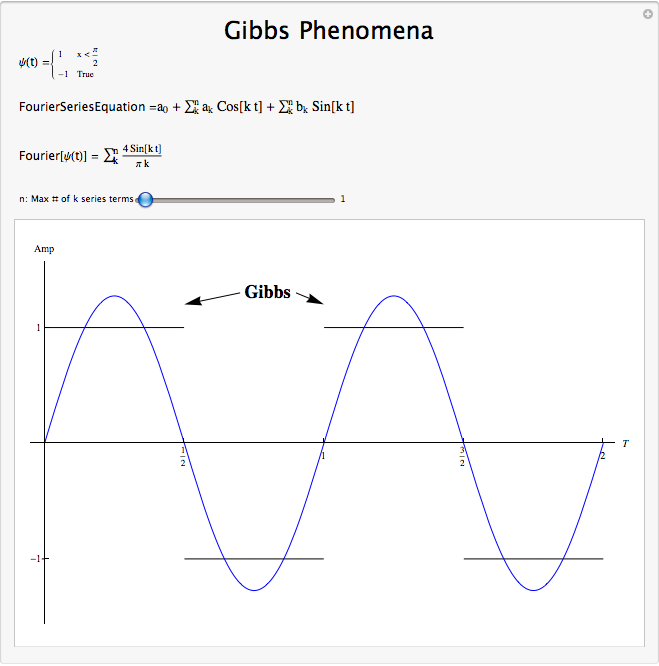
El siguiente VI demuestra la ocurrencia de Fenómenos de Gibb. Observe cómo los meneo cerca del pulso cuadrado a la izquierda permanecen incluso si aumenta drásticamente el orden de la aproximación, a pesar de que sí se vuelven más estrechos. También observe cómo la aproximación de la región lisa en el medio es mucho mejor que la de la región discontinua, especialmente en órdenes inferiores.

Figura\(\PageIndex{2}\): Interactuar (cuando esté en línea) con un CDF de Mathematica demostrando fenómenos de Gibbs. Para descargar, haz clic derecho y guarda como .cdf.

Conclusión

Podemos aproximar una función volviendo a sintetizar usando solo algunos de los coeficientes de Fourier (truncando el F.S.)

\[f_{N}^{\prime}(t)=\sum_{n n \leq|N|} c_{n} e^{j \omega_{0} n t} \nonumber \]

Esta aproximación funciona bien donde\(f(t)\) es continua, pero no tan bien donde\(f(t)\) es discontinua. En las regiones de discontinuidad, siempre encontraremos Fenómenos de Gibb, que nunca disminuyen por debajo del 9% de la altura de la discontinuidad, sino que se vuelven cada vez más estrechos a medida que agregamos más términos.