12.5: Polos y ceros en el Plano Z
- Page ID
- 86412
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción a los Polos y Ceros de la Transformación Z
Es bastante difícil analizar cualitativamente la transformada de Laplace (Sección 11.1) y la transformada Z, ya que las asignaciones de su magnitud y fase o parte real y parte imaginaria dan como resultado múltiples asignaciones de superficies bidimensionales en el espacio tridimensional. Por esta razón, es muy común examinar una trama de polos y ceros de una función de transferencia para tratar de hacerse una idea cualitativa de lo que hace un sistema.
Una vez que se ha determinado la transformación Z de un sistema, se puede utilizar la información contenida en los polinomios de la función para representar gráficamente la función y observar fácilmente muchas características definitorias. La transformada Z tendrá la siguiente estructura, basada en Funciones Racionales (Sección 12.7):
\[X(z)=\frac{P(z)}{Q(z)} \nonumber \]
Los dos polinomios,\(P(z)\) y\(Q(z)\), nos permiten encontrar los polos y ceros de la Transformación Z.
Definición: ceros
- El (los) valor (s) para\(z\) donde\(P(z)=0\).
- Las frecuencias complejas que hacen que la ganancia general de la función de transferencia de filtro sea cero.
Definición: polos
- El (los) valor (s) para\(z\) donde\(Q(z)=0\).
- Las frecuencias complejas que hacen que la ganancia general de la función de transferencia de filtro sea infinita.
Ejemplo\(\PageIndex{1}\)
A continuación se muestra una función de transferencia simple con los polos y ceros que se muestran debajo de ella.
\[H(z)=\frac{z+1}{\left(z-\frac{1}{2}\right)\left(z+\frac{3}{4}\right)} \nonumber \]
Los ceros son:\({−1}\)
Los polos son:\(\left\{\frac{1}{2},-\frac{3}{4}\right\}\)
El plano Z
Una vez que se han encontrado los polos y ceros para una Transformación Z dada, se pueden trazar en el Plano Z. El plano Z es un plano complejo con un eje imaginario y real que hace referencia a la variable de valor complejo\(z\). La posición en el plano complejo viene dada por\(re^{j \theta}\) y el ángulo desde el eje positivo real alrededor del plano se denota por\(\theta\). Al mapear polos y ceros en el plano, los polos se denotan con una “x” y los ceros por una “o”. La siguiente figura muestra el Plano Z, y ejemplos de trazar ceros y polos en el plano se pueden encontrar en la siguiente sección.
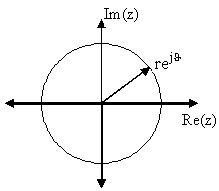
Figura\(\PageIndex{1}\)
Ejemplos de Gráficas de Polo/Cero
Esta sección enumera varios ejemplos de encontrar los polos y ceros de una función de transferencia y luego trazarlos en el Plano Z.
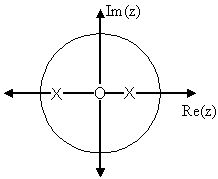
Ejemplo\(\PageIndex{2}\): Simple Pole/Zero Plot
\[H(z)=\frac{z}{\left(z-\frac{1}{2}\right)\left(z+\frac{3}{4}\right)} \nonumber \]
Los ceros son:\(\{0\}\)
Los polos son:\(\left\{\frac{1}{2},-\frac{3}{4}\right\}\)
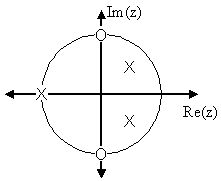
Ejemplo\(\PageIndex{3}\): Complex Pole/Zero Plot
\[H(z)=\frac{(z-j)(z+j)}{\left(z-\left(\frac{1}{2}-\frac{1}{2} j\right)\right)\left(z-\frac{1}{2}+\frac{1}{2} j\right)} \nonumber \]
Los ceros son:\(\{j,-j\}\)
Los polos son:\(\left\{-1, \frac{1}{2}+\frac{1}{2} j, \frac{1}{2}-\frac{1}{2} j\right\}\)
Ejemplo\(\PageIndex{4}\): Pole-Zero Cancellation
Un error fácil de cometer con respecto a polos y ceros es pensar que una función como\(\frac{(s+3)(s-1)}{s-1}\) es la misma que\(s+3\). En teoría son equivalentes, ya que el polo y cero al\(s=1\) cancelarse entre sí en lo que se conoce como cancelación polo-cero. No obstante, piense en lo que podría suceder si ésta fuera una función de transferencia de un sistema que fue creado con circuitos físicos. En este caso, es muy poco probable que el polo y el cero permanezcan exactamente en el mismo lugar. Un cambio menor de temperatura, por ejemplo, podría hacer que uno de ellos se mueva ligeramente. Si esto ocurriera se crea una tremenda cantidad de volatilidad en esa zona, ya que hay un cambio de infinito en el polo a cero en el cero en un rango muy pequeño de señales. Esta es generalmente una muy mala manera de tratar de eliminar un poste. Una manera mucho mejor es usar la teoría del control para mover el polo a un mejor lugar.
Nota: Polos y ceros repetidos
Es posible tener más de un polo o cero en cualquier punto dado. Por ejemplo, la función de transferencia de tiempo discreto\(H(z)=z^2\) tendrá dos ceros en el origen y la función de tiempo continuo\(H(s)=\frac{1}{s^{25}}\) tendrá 25 polos en el origen.
MATLAB - Si el acceso a MATLAB está fácilmente disponible, entonces puede usar sus funciones para crear fácilmente gráficas de polo/cero. A continuación se muestra un programa corto que traza los polos y ceros del ejemplo anterior en el Plano Z.
% Set up vector for zeros
z = [j ; -j];
% Set up vector for poles
p = [-1 ; .5+.5j ; .5-.5j];
figure(1);
zplane(z,p);
title('Pole/Zero Plot for Complex Pole/Zero Plot Example');
Demostración Interactiva de Polos y Ceros
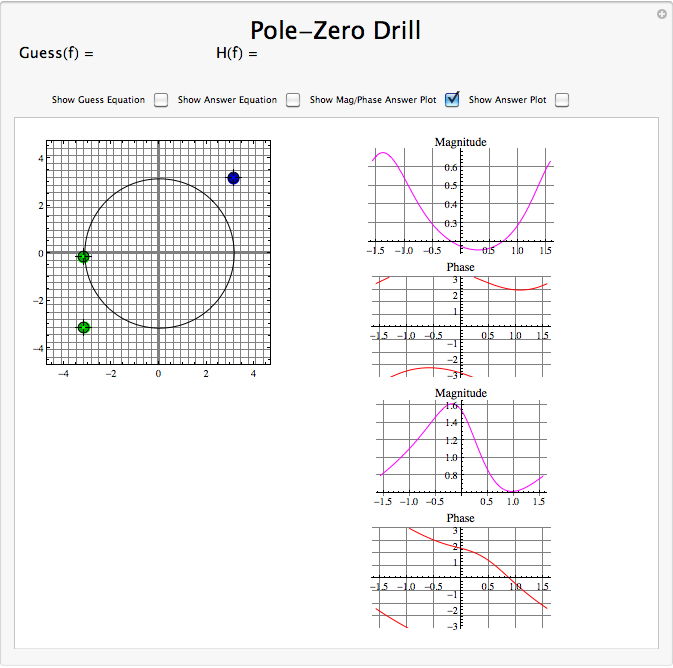
Aplicaciones para parcelas polo-cero
Teoría de Estabilidad y Control
Ahora que hemos encontrado y trazado los polos y ceros, debemos preguntarnos qué es lo que nos da esta trama. Básicamente lo que podemos deducir de esto es que la magnitud de la función de transferencia será mayor cuando esté más cerca de los polos y menor cuando esté más cerca de los ceros. Esto nos proporciona una comprensión cualitativa de lo que hace el sistema a diversas frecuencias y es crucial para la discusión de la estabilidad (Sección 3.6).
Parcelas Polo/Cero y la Región de Convergencia
La región de convergencia (ROC) para\(X(z)\) en el plano Z complejo se puede determinar a partir de la gráfica polo/cero. Si bien pueden ser posibles varias regiones de convergencia, donde cada una corresponde a una respuesta de impulso diferente, hay algunas opciones que son más prácticas. Se puede elegir un ROC para hacer que la función de transferencia sea causal y/o estable dependiendo de la gráfica polo/cero.
Filtrar Propiedades de ROC
- Si el ROC se extiende hacia afuera desde el polo más exterior, entonces el sistema es causal.
- Si el ROC incluye el círculo unitario, entonces el sistema es estable.
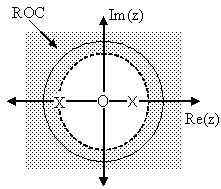
A continuación se muestra una gráfica polo/cero con un posible ROC de la transformada Z en la Gráfica Simple Polo/Cero (Ejemplo\(\PageIndex{2}\)) discutida anteriormente. La región sombreada indica el ROC elegido para el filtro. A partir de esta cifra, podemos ver que el filtro será tanto causal como estable ya que se cumplen ambas condiciones antes enumeradas.
Ejemplo\(\PageIndex{5}\)
\[H(z)=\frac{z}{\left(z-\frac{1}{2}\right)\left(z+\frac{3}{4}\right)} \nonumber \]
Respuesta de Frecuencia y Gráficas Polo/Cero
La razón por la que es útil entender y crear estas parcelas de polo/cero se debe a su capacidad para ayudarnos a diseñar fácilmente un filtro. Con base en la ubicación de los polos y ceros, la respuesta de magnitud del filtro se puede entender rápidamente. Además, al comenzar con la gráfica polo/cero, se puede diseñar un filtro y obtener su función de transferencia muy fácilmente.


