12.6: Región de Convergencia para la Transformación Z
- Page ID
- 86394
Introducción
Con la transformada z, el plano s representa un conjunto de señales (exponenciales complejos (Sección 1.8)). Para cualquier sistema LTI (Sección 2.1) dado, algunas de estas señales pueden hacer que la salida del sistema converja, mientras que otras hacen que la salida diverja (“explote”). El conjunto de señales que hacen que la salida del sistema converja se encuentra en la región de convergencia (ROC). Este módulo discutirá cómo encontrar esta región de convergencia para cualquier sistema LTI de tiempo discreto.
La Región de Convergencia
La región de convergencia, conocida como ROC, es importante de entender porque define la región donde existe la transformada z. La transformada z de una secuencia se define como
\[X(z)=\sum_{n=-\infty}^{\infty} x[n] z^{-n} \nonumber \]
El ROC para un dado\(x[n]\), se define como el rango\(z\) para el cual converge la transformada z. Dado que la transformada z es una serie de potencia, converge cuando\(x[n]z^{−n}\) es absolutamente sumable. Dicho de otra manera,
\[\sum_{n=-\infty}^{\infty}\left|x[n] z^{-n}\right|<\infty \nonumber \]
deben satisfacerse para la convergencia.
Inmuebles de la Región de Convergencec
La Región de Convergencia tiene una serie de propiedades que dependen de las características de la señal,\(x[n]\).
- El ROC no puede contener ningún polo. Por definición un polo es un donde\(X(z)\) es infinito. Ya que\(X(z)\) debe ser finito para todos\(z\) para la convergencia, no puede haber un polo en el ROC.
- Si\(\bf{x[n]}\) es una secuencia de duración finita, entonces el ROC es todo el plano z, excepto posiblemente\(\bf{z=0}\) o\(\bf{|z|=\infty}\). Una secuencia de duración finita es una secuencia que no es cero en un intervalo finito\(n_1≤n≤n_2\). Siempre y cuando cada valor de\(x[n]\) sea finito entonces la secuencia será absolutamente sumable. Cuando\(n_2>0\) habrá un\(z^{−1}\) término y por lo tanto el ROC no incluirá\(z=0\). Cuando\(n_1<0\) entonces la suma será infinita y así el ROC no incluirá\(|z|=\infty\). Por otro lado, cuando\(n_2≤0\) entonces el ROC incluirá\(z=0\), y cuándo incluirá\(n_1≥0\) el ROC\(|z|=\infty\). Con estas restricciones, es la única señal, entonces, cuyo ROC es todo el plano z\(x[n]=c \delta[n]\).
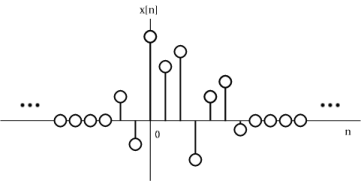
Las siguientes propiedades se aplican a secuencias de duración infinita. Como se señaló anteriormente, la transformada z converge cuando\(|X(z)|<\infty\). Así podemos escribir
\[|X(z)|=\left|\sum_{n=-\infty}^{\infty} x[n] z^{-n}\right| \leq \sum_{n=-\infty}^{\infty}\left|x[n] z^{-n}\right|=\sum_{n=-\infty}^{\infty}|x[n]|(|z|)^{-n} \nonumber \]
Entonces podemos dividir la suma infinita en porciones de tiempo positivo y tiempo negativo. Entonces
\[|X(z)| \leq N(z)+P(z) \nonumber \]
donde
\[N(z)=\sum_{n=-\infty}^{-1}|x[n]|(|z|)^{-n} \nonumber \]
y
\[P(z)=\sum_{n=0}^{\infty}|x[n]|(|z|)^{-n} \nonumber \]
\(|X(z)|\)Para que sea finito,\(|x[n]|\) debe ser acotado. Entonces vamos a establecer
\[|x(n)| \leq C_{1} r_{1}^{n} \nonumber \]
para
\[n<0 \nonumber \]
y
\[|x(n)| \leq C_{2} r_{2}^{n} \nonumber \]
para
\[n≥0 \nonumber \]
De esto se pueden derivar algunas propiedades adicionales:
- Si\(\bf{x[n]}\) es una secuencia del lado derecho, entonces el ROC se extiende hacia afuera desde el polo más externo en\(\bf{X(z)}\). Una secuencia del lado derecho es una secuencia donde\(x[n]=0\) para\(n<n_1<\infty\). Al observar la porción de tiempo positivo de la derivación anterior, se deduce que
\[P(z) \leq C_{2} \sum_{n=0}^{\infty} r_{2}^{n}(|z|)^{-n}=C_{2} \sum_{n=0}^{\infty}\left(\frac{r_{2}}{|z|}\right)^{n} \nonumber \]
Así, para que esta suma converja\(|z|>r_2\), y por lo tanto el ROC de una secuencia del lado derecho es de la forma\(|z|>r_2\).
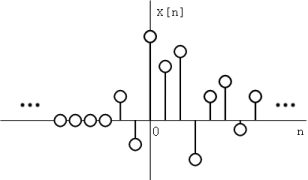
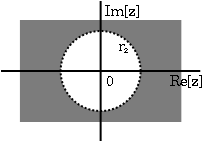
- Si\(\bf{x[n]}\) es una secuencia del lado izquierdo, entonces el ROC se extiende hacia adentro desde el polo más interno en\(\bf{X(z)}\). Una secuencia del lado izquierdo es una secuencia donde\(x[n]=0\) para\(n>n_2>−\infty\). Al observar la porción de tiempo negativo de la derivación anterior, se deduce que
\[N(z) \leq C_{1} \sum_{n=-\infty}^{-1} r_{1}^{n}(|z|)^{-n}=C_{1} \sum_{n=-\infty}^{-1}\left(\frac{r_{1}}{|z|}\right)^{n}=C_{1} \sum_{k=1}^{\infty}\left(\frac{|z|}{r_{1}}\right)^{k} \nonumber \]
Así, para que esta suma converja\(|z|<r_1\), y por lo tanto el ROC de una secuencia del lado izquierdo es de la forma\(|z|<r_1\).
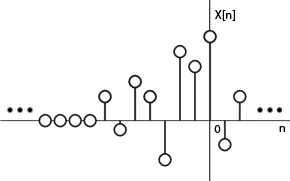
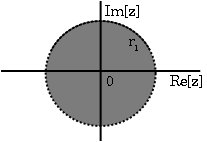
- Si\(\bf{x[n]}\) es una secuencia de dos lados, el ROC será un anillo en el plano z que está delimitado en el interior y el exterior por un poste. Una secuencia de dos lados es una secuencia con duración infinita en las direcciones positiva y negativa. De la derivación de las dos propiedades anteriores, se deduce que si\(-r_2<|z|<r_2\) converge, entonces ambas porciones positivo-tiempo y negativo convergen y así\(X(z)\) convergen también. Por lo tanto, el ROC de una secuencia bilateral es de la forma\(-r_2<|z|<r_2\).
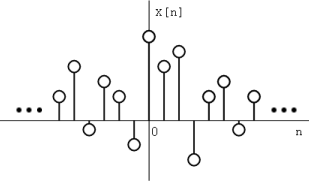
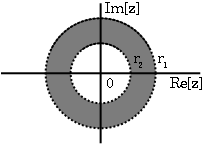
Ejemplos
Ejemplo\(\PageIndex{1}\)
Tomemos
\[x_{1}[n]=\left(\frac{1}{2}\right)^{n} u[n]+\left(\frac{1}{4}\right)^{n} u[n] \nonumber \]
La transformada z de\(\left(\frac{1}{2}\right)^{n} u[n]\) es\(\frac{z}{z-\frac{1}{2}}\) con un ROC en\(|z|>\frac{1}{2}\).
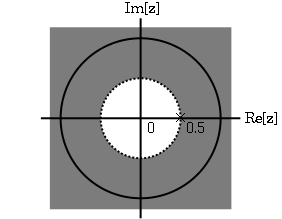
La transformada z de\(\left(\frac{-1}{4}\right)^{n} u[n]\) es\(\frac{z}{z+\frac{1}{4}}\) con un ROC en\(|z|>\frac{-1}{4}\).
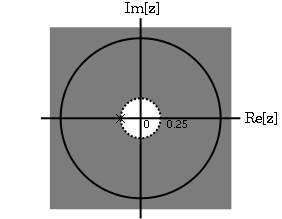
Debido a la linealidad,
\ [\ begin {align}
X_ {1} [z] &=\ frac {z} {z} {z-\ frac {1} {2}} +\ frac {z} {z+\ frac {1} {4}}\ nonumber\\
&=\ frac {2 z\ izquierda (z-\ frac {1} {8}\ derecha)} {\ izquierda (z-\ frac {1} {2}\ derecha)\ izquierda (z+\ frac {1} {4}\ derecha)}
\ end {align}\ nonumber\]
Por observación es claro que hay dos ceros, at\(0\) y\(\frac{1}{8}\), y dos polos, at\(\frac{1}{2}\), y\(\frac{−1}{4}\). Siguiendo las propiedades obove, el ROC es\(|z|>\frac{1}{2}\).
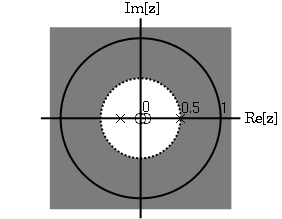
Ejemplo\(\PageIndex{2}\)
Ahora toma
\[x_{2}[n]=\left(\frac{-1}{4}\right)^{n} u[n]-\left(\frac{1}{2}\right)^{n} u[(-n)-1] \nonumber \]
La transformada z y ROC de\(\left(\frac{-1}{4}\right)^{n} u[n]\) se mostraron en el ejemplo anterior. El transormo z de\(\left(-\left(\frac{1}{2}\right)^{n}\right) u[(-n)-1]\) es\(\frac{z}{z-\frac{1}{2}}\) con un ROC en\(|z|>\frac{1}{2}\).
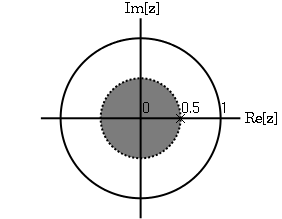
Una vez más, por linealidad,
\ [\ begin {align}
X_ {2} [z] &=\ frac {z} {z+\ frac {1} {4}} +\ frac {z} {z-\ frac {1} {2}}\ nonumber\\
&=\ frac {z\ left (2 z-\ frac {1} {8}\ derecha)} {\ izquierda (z+\ frac {1} {4}\ derecha)\ izquierda (z-\ frac {1} {2}\ derecha)}
\ end {align}\ nonumber\]
Por observación vuelve a quedar claro que hay dos ceros, a\(0\) y\(\frac{1}{16}\), y dos polos, at\(\frac{1}{2}\), y\(\frac{−1}{4}\). aunque en este caso, el ROC lo es\(|z|<\frac{1}{2}\).
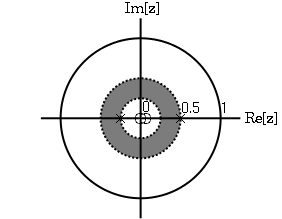
Comprensión gráfica de ROC
Usando la demostración, aprenda sobre la región de convergencia para la Transformación de Laplace.
Conclusión
Claramente, para elaborar un sistema que sea realmente útil en virtud de ser causal y BIBO estable, debemos asegurarnos de que esté dentro de la Región de Convergencia, lo que se puede determinar mirando la trama del polo cero. La Región de Convergencia es el área en la gráfica polo/cero de la función de transferencia en la que existe la función. Para fines de útil diseño de filtros, preferimos trabajar con funciones racionales, las cuales pueden ser descritas por dos polinomios, uno cada uno para determinar los polos y los ceros, respectivamente.


