15.3: Normas

Introducción

Este módulo explicará normas, un concepto matemático que proporciona una noción del tamaño de un vector. Específicamente, se discutirá la definición general de una norma y se presentarán normas discretas de señal de tiempo.

Normas

La norma de un vector es un número real que representa el “tamaño” del vector.

Ejemplo\(\PageIndex{1}\)

En\(\mathbb{R}^2\), podemos definir una norma para ser una longitud geométrica de vectores.

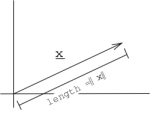
Figura\(\PageIndex{1}\)

\(\boldsymbol{x}=(x_0,x_1)^T\), norma\(\|\boldsymbol{x}\|=\sqrt{x_{0}^{2}+x_{1}^{2}}\)

Matemáticamente, una norma\(\|\cdot\|\) es solo una función (tomar un vector y devolver un número real) que satisface tres reglas.

Para ser una norma,\(\|\cdot\|\) debe satisfacer:

1. la norma de cada vector es positiva\(\|x\|>0\),\(x \in S\)
2. escalar un vector escala la norma por la misma cantidad\(\|\alpha x\|=|\alpha|\|x\|\) para todos los vectores\(x\) y escalares\(\alpha\)
3. Triángulo Propiedad:\(\|x+y\| \leq\|x\|+\|y\|\) para todos los vectores\(x\),\(y\). “El “tamaño” de la suma de dos vectores es menor o igual a la suma de sus tamaños”

Un espacio vectorial (Sección 15.2) con una norma bien definida se denomina espacio vectorial normado o espacio lineal normado.

Ejemplos

Ejemplo\(\PageIndex{2}\)

\(\mathbb{R}^n\)(o\(\mathbb{C}^n\)),\ (\ negridsymbol {x} =\ left (\ begin {array} {c}
x_ {0}\\
x_ {1}\
\\ puntos\\
x_ {n-1}
\ end {array}\ derecha)\)\(\|x\|_{1}=\sum_{i=0}^{n-1}\left|x_{i}\right|\),\(\mathbb{R}^n\) con esta norma se llama\(\ell^{1}([0, n-1])\).

Figura\(\PageIndex{2}\): Colección de todos\(\boldsymbol{x} \in \mathbb{R}^2\) con\(\|x\|_{1}=1\)

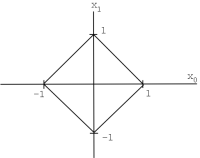
Ejemplo\(\PageIndex{3}\)

\(\mathbb{R}^n\)(o\(\mathbb{C}^n\)), con norma\(\|x\|_{2}=\left(\sum_{i=0}^{n-1}\left(\left|x_{i}\right|\right)^{2}\right)^{\frac{1}{2}}\),\(\mathbb{R}^n\) se llama\(\ell^{2}([0, n-1])\) (la habitual norma “euclidiana”).

Figura\(\PageIndex{3}\): Colección de todos\(\boldsymbol{x} \in \mathbb{R}^{2}\) con\(\|x\|_{2}=1\)

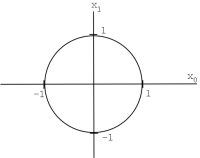
Ejemplo\(\PageIndex{4}\)

\(\mathbb{R}^n\)(o\(\mathbb{C}^n\)), con norma\(\|x\|_{\infty}=\max _{i}\left\{i,\left|x_{i}\right|\right\}\) se llama\(\ell^{\infty}([0, n-1])\)

Figura\(\PageIndex{4}\):\(x \in \mathbb{R}^2\) con\(\|x\|_{\infty}=1\)

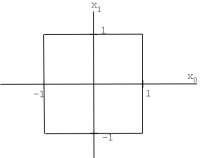
Espacios de Secuencias y Funciones

Podemos definir normas similares para espacios de secuencias y funciones.

Señales de tiempo discretas = secuencias de números

\[x[n]=\left\{\ldots, x_{-2}, x_{-1}, x_{0}, x_{1}, x_{2}, \ldots\right\} \nonumber \]

• \(\|x(n)\|_{1}=\sum_{i=-\infty}^{\infty}|x[i]|, x[n] \in \ell^{1}(\mathbb{Z}) \Rightarrow\left(\|x\|_{1}<\infty\right)\)
• \(\|x(n)\|_{2}=\left(\sum_{i=-\infty}^{\infty}(|x[i]|)^{2}\right)^{\frac{1}{2}}, x[n] \in \ell^{2}(\mathbb{Z}) \Rightarrow\left(\|x\|_{2}<\infty\right)\)
• \(\|x(n)\|_{p}=\left(\sum_{i=-\infty}^{\infty}(|x[i]|)^{P}\right)^{\frac{1}{p}}, x[n] \in \ell^{p}(\mathbb{Z}) \Rightarrow\left(\|x\|_{p}<\infty\right)\)
• \(\|x(n)\|_{\infty}=\sup _{i}|x[i]|, x[n] \in \ell^{\infty}(\mathbb{Z}) \Rightarrow\left(\|x\|_{\infty}<\infty\right)\)

Para funciones de tiempo continuo:

• \(\|f(t)\|_{p}=\left(\int_{-\infty}^{\infty}(|f(t)|)^{p} d t\right)^{\frac{1}{p}}, f(t) \in L^{p}(\mathbb{R}) \Rightarrow\left(\|f(t)\|_{p}<\infty\right)\)
• \(\|f(t)\|_{p}=\left(\int_{0}^{T}(|f(t)|)^{p} d t\right)^{\frac{1}{p}}, f(t) \in L^{p}([0, T]) \Rightarrow\left(\|f(t)\|_{p}<\infty\right)\)