15.2: Espacios vectoriales

Introducción

Definición: Espacio vectorial

Un espacio vectorial\(S\) es una colección de “vectores” de tal manera que (1) si\(f_{1} \in S \Rightarrow \alpha f_{1} \in S\) para todos los escalares\(\alpha\) (donde\(alpha \in \mathbb{R}\)\(\alpha \in \mathbb{C}\), o algún otro campo) y (2) si\(f_{1} \in S\),\(f_2 \in S\), entonces\((f_1+f_2) \in S\)

Para definir un espacio vectorial, necesitamos

• Un conjunto de cosas llamadas “vectores” (\(X\))
• Un conjunto de cosas llamadas “escalares” que forman un campo (\(A\))
• Una operación de adición vectorial ()
• Una operación de multiplicación escalar (\(*\))

Las operaciones necesitan tener todas las propiedades que se dan a continuación. El cierre suele ser lo más importante para mostrar.

Espacios vectoriales

Si los escalares\(\alpha\) son reales,\(S\) se llama espacio vectorial real.

Si los escalares\(\alpha\) son complejos,\(S\) se llama un espacio vectorial complejo.

Si los “vectores” en\(S\) son funciones de una variable continua, a veces llamamos\(S\) un espacio de función lineal

Propiedades

Definimos un conjunto\(V\) para ser un espacio vectorial si

1. \(x+y=y+x\)para cada uno\(x\) y\(y\) en\(V\)
2. \(x+(y+z)=(x+y)+z\)para cada uno\(x\),\(y\), y\(z\) en\(V\)
3. Hay un “vector cero” único tal que\(x+0=x\) para cada uno\(x\) en\(V\) (0 es la identidad aditiva de campo)
4. Para cada uno\(x\)\(V\) hay un vector único\(−x\) tal que\(x+−x=0\)
5. \(1x=x\)(1 es la identidad multiplicativa de campo)
6. \((c_1c_2)x=c_1(c_2x)\)para cada uno\(x\) en\(V\)\(c_1\) y\(c_2\) en\(\mathbb{C}\)
7. \(c(x+y)=cx+cy\)para cada uno\(x\) y\(y\) en\(V\) y\(c\) en\(\mathbb{C}\)
8. \((c_1+c_2)x=c_1x+c_2x\)para cada uno\(x\) en\(V\)\(c_1\) y\(c_2\) en\(\mathbb{C}\)

Ejemplos

• \(\mathbb{R}^n\)= espacio vectorial real
• \(\mathbb{C}^n\)= espacio vectorial complejo
• \(L^{1}(\mathbb{R})=\left\{f(t), f(t) | \int_{-\infty}^{\infty}\left| f(t) \right| \mid d t<\infty\right\}\)es un espacio vectorial
• \(L^{\infty}(\mathbb{R})=\{f(t), f(t) \mid f(t) \text { is bounded }\}\)es un espacio vectorial
• \(L^{2}(\mathbb{R})=\left\{f(t), f(t) | \int_{-\infty}^{\infty}(|f(t)|)^{2} d t<\infty\right\}\)= señales de energía finita es un espacio vectorial
• \(L^{2}([0, T])\)= funciones de energía finita en el intervalo\([0,T]\)
• \(\ell^{1}(\mathbb{Z})\),\(\ell^{2}(\mathbb{Z})\),\(\ell^{\infty}(\mathbb{Z})\) son espacios vectoriales
• La colección de funciones por partes constante entre los enteros es un espacio vectorial

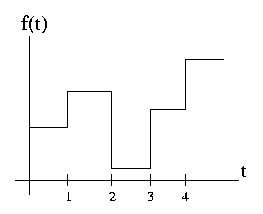
Figura\(\PageIndex{1}\)

• \ (\ mathbb {R} _ {+} ^ {2} =\ left\ {\ left (\ begin {array} {l}
  x_ {0}\\
  x_ {1}
  \ end {array}\ right),\ left (\ begin {array} {l}
  x_ {0}\
  x_ {1}
  \ end {array}\ derecha)\ mid\ left (x_ {0} >0\ derecha)\ cuña\ izquierda (x_ {1} >0\ derecha)\ derecha\ }\) no es un espacio vectorial. \ (\ left (\ begin {array} {l}
  1\\
  1
  \ end {array}\ derecha)\ in\ mathbb {R} _ {+} ^ {2}\), pero\ (\ alpha\ left (\ begin {array} {l}
  
  1\
  \ end {array}\ right)\ notin\ mathbb {R} _ _ {+} ^ {2}\),\(\alpha < 0\)
• \(D=\left\{z \in \mathbb{C},|z| \leq 1\right\}\)no es un espacio vectorial. \(\left(z_{1}=1\right) \in D\),\((z_2=j) \in D\), pero\(\left(z_{1}+z_{2}\right) \notin D\),\(\left|z_{1}+z_{2}\right|=\sqrt{2}>1\)

Nota

Los espacios vectoriales pueden ser colecciones de funciones, colecciones de secuencias, así como colecciones de vectores tradicionales (es decir, listas finitas de números)