2.4: Las identidades de Euler y De Moivre
- Page ID
- 82167
Las identidades de Euler y De Moivre son las identidades fundamentales para derivar fórmulas trigonométricas. A partir de la identidad\(e^{jθ}=\cosθ+j\sinθ\) y la identidad conjugada\(e^{−jθ}=(e^{jθ})^∗=\cosθ−j\sinθ\), tenemos las identidades de Euler para\(\cosθ\) y\(\sinθ\):
\[\cosθ=\frac {e^{jθ}+e^{−jθ}} {2} \nonumber \]
\[\sinθ=\frac {e^{jθ}−e^{−jθ}} {2j} \nonumber \]
Estas identidades se ilustran en la Figura.
La identidad\(e^{jθ}=\cosθ+j\sinθ\) también produce la identidad De Moivre:
\[(\cosθ+j\sinθ)n=(e^{jθ})^n=e^{jnθ}=\cos nθ+j\sin nθ \nonumber \]
Cuando el lado izquierdo de esta ecuación se expande con la expansión binomial, obtenemos la identidad
\[∑_{k=0}^n \begin{pmatrix}n\\k\end{pmatrix} (cosθ)n−k(jsinθ)k=cosnθ+jsinnθ \nonumber \]
Coeficientes Binomiales y Triángulo de Pascal
Los coeficientes binomiales (nk) en la Ecuación son la taquigrafía del número
\[\begin{pmatrix}n\\k\end{pmatrix}=n!(n−k)!k!'k=0,1,...,n \nonumber \]
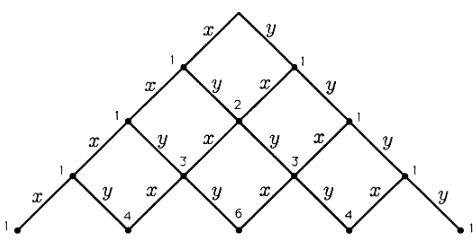
Este número da el coeficiente de\(x^{n−k}y^k\) en la expansión de\((x+y)^n\). ¿Cómo sabemos que hay\(\begin {pmatrix} n\\k\end {pmatrix}\) términos del formulario\(x^{n−k}y^k\)? Una forma de responder a esta pregunta es usar el triángulo de Pascal, ilustrado en la Figura. Cada nodo en el triángulo de Pascal muestra el número de rutas que terminan en ese nodo. Este número es siempre la suma del número de rutas que terminan en los nodos justo por encima del nodo en cuestión. Si pensamos en una trayectoria de la izquierda como una ocurrencia de una x y una trayectoria de la derecha como una ocurrencia de una y, entonces vemos que el triángulo de Pascal realiza un seguimiento del número de ocurrencias de\(x^{n−k}y^k\).
Demostrar\(\begin{pmatrix}n\\k\end{pmatrix}=(n^{n−k})\).
Encuentra una identidad para\(\begin{pmatrix}n−1\\k−1\end{pmatrix}+\begin{pmatrix}k\\n−1)\end{pmatrix}\).
Encuentra fórmulas de “medio ángulo” para\(\cos2θ\) y\(\sin2θ\).
Demostrar que
- \(\cos3θ=\cos^2θ−3 \cosθ\sin2θ\)
- \(\sin3θ=34\cos^2θ \sinθ−\sin3θ\)


