4.5: Proyecciones

Última actualización
Guardar como PDF

Page ID: 82480

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ortogonalidad

Cuando el ángulo entre dos vectores es\(\frac π 2\) o\(90^0\), decimos que los vectores son ortogonales. Un vistazo rápido a la definición de ángulo (Ecuación 12 de “Álgebra lineal: cosenos de dirección”) conduce a esta definición equivalente para ortogonalidad:

\[(x,y)=0⇔x\; \mathrm{and}\;y\;\mathrm{are\;orthogonal}. \nonumber \]

Por ejemplo, en la Figura 1 (a), los vectores\(x=\begin{bmatrix}3\\1\end{bmatrix}\) y\(y=\begin{bmatrix}-2\\6\end{bmatrix}\) son claramente ortogonales, y su producto interno es cero:

\[(x,y)=3(−2)+1(6)=0 \nonumber \]

En la Figura 1 (b), los vectores\(x=\begin{bmatrix}3\\1\\0\end{bmatrix}\)\(y=\begin{bmatrix}−2\\6\\0\end{bmatrix}\), y\(z=\begin{bmatrix}0\\0\\4\end{bmatrix}\) son mutuamente ortogonales, y el producto interno entre cada par es cero:

\[(x,y)=3(−2)+1(6)+0(0)=0 \nonumber \]

\[(x,z)=3(0)+1(0)+0(4)=0 \nonumber \]

\[(y,z)=−2(0)+6(0)+0(4)=0 \nonumber \]

La figura una parte a es una gráfica cartesiana con x_1 como eje horizontal y x_2 como eje vertical. Del origen al primer cuadrante se encuentra un vector etiquetado x con la matriz 2 por 1 3, 1. Del origen al segundo cuadrante hay un vector etiquetado y con la matriz 2 por 1 -2 6. — Figura\(\PageIndex{1}\): Ortogonalidad de Vectores.

La figura una parte b es una gráfica tridimensional con x_1 como eje apuntando, x_2 apuntando a la derecha y x_3 apuntando hacia arriba. El vector z sigue el eje x_3 hacia arriba, y se etiqueta con la matriz 3 por 1 0 0 4. El vector y apunta a lo largo del eje x_2 x_3 con una pendiente positiva y se etiqueta con una matriz de 3 por 1, -2 6 0. El vector x señala hacia fuera y a la derecha en el plano x_1 x_2 y se etiqueta con la matriz 3 por 1 3 1 0. — Figura\(\PageIndex{1}\): Ortogonalidad de Vectores.

Ejercicio\(\PageIndex{1}\)

Cuál de los siguientes pares de vectores es ortogonal:

\(x=\begin{bmatrix}1\\0\\1\end{bmatrix},y=\begin{bmatrix}0\\1\\0\end{bmatrix}\)
\(x=\begin{bmatrix}1\\1\\0\end{bmatrix},y=\begin{bmatrix}1\\1\\1\end{bmatrix}\)
\(x=e_1,y=e_3\)
\(x=\begin{bmatrix}a\\b\end{bmatrix} , y=\begin{bmatrix}−b\\a\end{bmatrix}\)

Podemos usar el producto interno para encontrar la proyección de un vector sobre otro como se ilustra en la Figura 2. Geométricamente encontramos la proyección de\(x\) sobre\(y\) dejando caer una perpendicular desde la cabeza de\(x\) sobre la línea que contiene\(y\). La perpendicular es la línea discontinua en la figura. El punto donde la perpendicular se cruza\(y\) (o una extensión de\(y\)) es la proyección de\(x\) hacia\(y\), o el componente de\(x\) lo largo\(y\). Vamos a llamarlo\(z\).

La figura dos es una gráfica bidimensional que contiene tres vectores en el primer cuadrante. El primero, x, comienza desde el origen y tiene una pendiente positiva pronunciada. El segundo, z, también comienza desde el origen y tiene una pendiente positiva más superficial. El ángulo entre z y x está etiquetado como θ. El tercero, y, comienza desde el final de z y se extiende con la misma pendiente que z más adentro del primer cuadrante. — Figura\(\PageIndex{2}\): Componente de un vector a lo largo de otro

Ejercicio\(\PageIndex{1}\)

Dibuja una figura como la Figura 2 mostrando la proyección de y sobre x.

El vector\(z\) se encuentra a lo largo\(y\), por lo que podemos escribirlo como el producto de su norma\(||z||\) y su vector de dirección\(u_y\):

\[z=||z||u_y=||z||\frac {y} {||y||} \nonumber \]

Pero, ¿qué es la norma\(||z||\)? De la Figura 2 vemos que el vector\(x\) es justo\(z\), más un vector\(v\) que es ortogonal a\(y\):

\[x=z+v,(v,y)=0 \nonumber \]

Por lo tanto, podemos escribir el producto interno entre\(x\) y\(y\) como

\[(x,y)=(z+v,y)=(z,y)+(v,y)=(z,y) \nonumber \]

Pero porque\(z\) y\(y\) ambos se encuentran\(y\), podemos escribir el producto interno\((x,y)\) como

\[(x,y)=(z,y)=(||z||u_y,||y||u_y)=||z||||y||(u_y,u_y)=||z||||y||||u_y||^2=||z||||y|| \nonumber \]

A partir de esta ecuación podemos resolver\(||z||=(x,y)||y||\) y sustituir\(||z||\) en Ecuación\(\PageIndex{6}\) para escribir\(z\) como

\[z=||z||\frac y {||y||}=\frac {(x,y)}{||y||} \frac y {||y||}= \frac {(x,y)}{(y,y)}y \nonumber \]

\(\PageIndex{10}\)La ecuación es lo que queríamos—una expresión para la proyección de\(x\) sobre\(y\) en términos de\(x\) y\(y\).

Ejercicio\(\PageIndex{1}\)

Demostrar eso\(||z||\) y\(z\) puede escribirse en términos de\(\cosθ\) para\(θ\) como se ilustra en la Figura 2:

\(||z||=||x||\cosθ\)

\(z=\frac {||x||\cosθ}{||y||}y\)

Descomposición ortogonal

Ya sabes cómo descomponer un vector en términos de los vectores de coordenadas unitarias,

\[\mathrm{x}=\left(\mathrm{x}, \mathrm{e}_{1}\right) \mathrm{e}_{1}+\left(\mathrm{x}, \mathrm{e}_{2}\right) \mathrm{e}_{2}+\cdots+\left(\mathrm{x}, \mathrm{e}_{n}\right) \mathrm{e}_{n} \nonumber \]

En esta ecuación, (x,\(e_k\))\(e_k\) (x, ek) ek es el componente de\(x\) along\(e_k\), o la proyección de\(x\) onto\(e_k\), pero el conjunto de vectores de coordenadas unitarias no es la única base posible para descomponer un vector. Consideremos un par arbitrario de vectores ortogonales\(x\) y\(y\):

\((\mathrm{x}, \mathrm{y})=0\).

La suma de\(x\) y\(y\) produce un nuevo vector\(w\), ilustrado en la Figura 3, donde se ha utilizado un dibujo bidimensional para representar\(n\) dimensiones. La norma al cuadrado de\(w\) es

\ [\ begin {alineado}
\ |\ mathrm {w}\ |^ {2} & =(\ mathrm {w},\ mathrm {w}) = [(\ mathrm {x} +\ mathrm {y}), (\ mathrm {x} +\ mathrm {y})] =(\ mathrm {x},\ mathrm {x}) + (\ mathrm {x},\ mathrm {y}) + (\ mathrm {y},\ mathrm {x}) + (\ mathrm {y},\ mathrm {y})\\
&=\ quad\ |\ mathrm {x}\ |^ {2} +\ |\ mathrm {y}\ |^ {2}
\ end {alineado}\ nonumber\]

¡Este es el teorema de Pitágoras en\(n\) dimensiones! La longitud al cuadrado de\(w\) es solo la suma de los cuadrados de las longitudes de sus dos componentes ortogonales.

Screen Shot 2021-08-04 a las 11.00.45 PM.png — Figura\(\PageIndex{3}\): Suma de vectores ortogonales

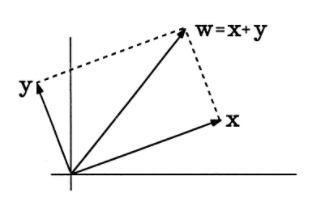
La proyección de\(w\) sobre\(x\) es\(x\), y la proyección de\(w\) sobre\(y\) es\(y\):

\(w=(1) x+(1) y\)

Si escalamos\(w\) por\(a\) para producir el vector z=\(a\) w, la descomposición ortogonal de\(z\) es

\(\mathrm{z}=a \mathrm{w}=(\mathrm{a}) \mathrm{x}+(\mathrm{a}) \mathrm{y}\).

Vamos a darle la vuelta a este argumento. En lugar de construir\(w\) a partir de vectores ortogonales\(x\) y\(y\), comencemos con arbitrarios\(w\)\(x\) y y veamos si podemos calcular una descomposición ortogonal. La proyección de\(w\) sobre\(x\) se encuentra desde\(\mathrm{z}=\frac{\|\mathrm{x}\| \cos \theta}{\|\mathrm{y}\|} \mathrm{y}\).

\[w_{x}=\frac{(w, x)}{(x, x)} x \nonumber \]

Pero debe haber otro componente de\(w\) tal que\(w\) sea igual a la suma de los componentes. Llamemos al componente desconocido\(w_y\). Entonces

\[\mathrm{w}=\mathrm{w}_{\mathrm{x}}+\mathrm{w}_{\mathrm{y}} \nonumber \]

Ahora, como sabemos\(w\) y\(w_x\) ya, nos encontramos\(w_y\) con ser

\[\mathrm{w}_{\mathrm{y}}=\mathrm{w}-\mathrm{w}_{\mathrm{x}}=\mathrm{w}-\frac{(\mathrm{w}, \mathrm{x})}{(\mathrm{x}, \mathrm{x})} \mathrm{x} \nonumber \]

Curiosamente, la forma en que nos hemos descompuesto siempre\(w\) producirá\(w_x\) y\(w_{>y}\) ortogonales entre sí. Comprobemos esto:

\ [\ begin {array} {l}
\ begin {alineado}
\ left (\ mathrm {w} _ {\ mathrm {x}},\ mathrm {w} _ {\ mathrm {y}}\ right) &=\ left (\ frac {(\ mathrm {w},\ mathrm {x})} {(\ mathrm {x},\ mathrm {x})}\ mathrm {x},\ mathrm {w} -\ frac {(\ mathrm {w},\ mathrm {x})} {(\ mathrm {x},\ mathrm {x})}\ mathrm {x}\ derecha)\\
&=\ frac {(\ mathrm {w},\ mathrm {x})} {(\ mathrm {x},\ mathrm {x})} (\ mathrm {x},\ mathrm {w}) -\ frac {(\ mathrm {w},\ mathrm {x}) ^ {2}} {(\ mathrm {x},\ mathrm {x}) ^ {2}} (\ mathrm {x},\ mathrm {x})\\
&=\ quad\ frac {(\ mathrm {w},\ mathrm {x}) ^ {2}} {(\ mathrm {x},\ mathrm {x})} -\ frac {(\ mathrm {w},\ mathrm {x}) ^ {2}} (\ mathrm {x},\ mathrm {x})}\\
&=\ qquad\ qquad 0
\ end {alineado}\\
\ end {array}\ nonumber\]

Para resumir, hemos tomado dos vectores arbitrarios,\(w\) y\(x\), y descompuesto\(w\) en un componente en la dirección de\(x\) y un componente ortogonal a\(x\).