6.6: Secuencias de prueba
- Page ID
- 82410
Cuando diseñamos un filtro, lo diseñamos para un propósito. Por ejemplo, un filtro de promedio móvil a menudo está diseñado para pasar datos relativamente constantes mientras se promedian datos relativamente variables. En un esfuerzo por aclarar el comportamiento de un filtro, normalmente analizamos su respuesta a un conjunto estándar de señales de prueba. Llamaremos al impulso, al paso y al complejo exponencial las señales de prueba estándar.
Secuencia de impulsos unitarios
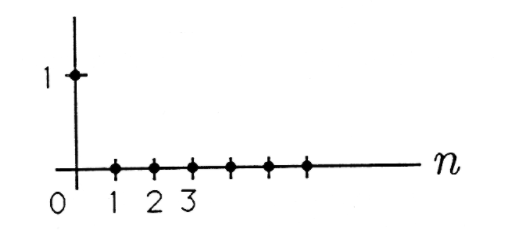
La secuencia de impulsos unitarios es la secuencia
\[u_{n}=\delta_{n}= \begin{cases}1, & n=0 \\ 0, & n \neq 0\end{cases} \nonumber \]
Esta secuencia, ilustrada en la Figura 1, consiste en todos los ceros excepto por uno solo en\(n=0\). Si la secuencia de impulsos unitarios se pasa a través de un filtro de promedio móvil (ya sea finito o no), entonces la salida se denomina respuesta de pulso unitario:
\ [\ begin {align}
h_ {n} &=\ suma_ {k=0} ^ {\ infty} w_ {k}\ delta_ {n-k}\ nonumber\\
&=w_ {n}
\ end {align}\ nonumber\]
(Tenga en cuenta que\(\delta_{n-k}=0\) a menos que\(n=k\).) Por lo tanto, la secuencia de impulsos unitarios se puede utilizar para leer los pesos de un filtro de media móvil. Es práctica común usar\(w_k\) (la\(k^{\text {th }}\) y\(h_k\) (la respuesta al\(k^{\text {th }}\) impulso) indistintamente.
Encuentre la respuesta de pulso unitario para la media móvil finita\(x_{n}=\sum_{k=0}^{N-1} w_{k} u_{n-k}\). Precaución: Debe considerar\(n<0,0 \leq n \leq N-1\), y\(n \geq N\).
Encuentre la respuesta de pulso unitario para el filtro recursivo\(x_{n}=a x_{n-1}+w_{0} u_{n}\).
Secuencia de pasos unitarios
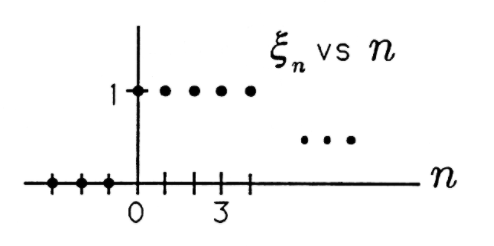
La secuencia de pasos unitarios es la secuencia
\[u_{n}=\xi_{n}= \begin{cases}1, & n \geq 0 \\ 0, & n<0\end{cases} \nonumber \]
Esta secuencia se ilustra en la Figura 2. Cuando esta secuencia se aplica a un filtro de promedio móvil, el resultado es la respuesta de paso unitario
\ [\ begin {align}
g_ {n} &=\ suma_ {k=0} ^ {n} w_ {k}\ nonumber\\
&=\ sum_ {k=0} ^ {n} h_ {k}.
\ end {align}\ nonumber\]
La respuesta de paso de unidad es solo la secuencia de sumas parciales de la respuesta de pulso unitario.
Encuentre la respuesta de paso unitario para el filtro de promedio móvil finito\(x_{n}=\sum_{k=0}^{N-1} w_{k} u_{n-k}\). Especializa tu resultado general al caso especial donde\(w_{k}=\frac{1}{N}\) para\(k=0,1, \ldots, N-1\).
Encuentre la respuesta de paso de unidad para el filtro recursivo\(x_{n}=a x_{n-1}+w_{0} u_{n}\).
Secuencia Exponencial Compleja
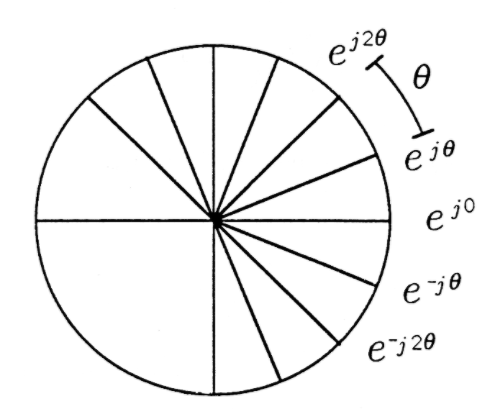
La secuencia exponencial compleja es la secuencia
\[u_{k}=e^{j k \theta}, k=0, \pm 1, \pm 2, \ldots \nonumber \]
Esta secuencia, ilustrada en la Figura 3, es un “fasor de tiempo discreto” que se “engancha” en sentido antihorario (CCW) a medida que\(k\) se mueve hacia\(k+1\) y hacia la derecha (CW) a medida que\(k\) se mueve hacia\(k-1\). Cada vez que los trinquetes fasores, resulta un ángulo de\(\theta\). ¿Por qué tal secuencia debería ser una secuencia de prueba útil? Hay dos razones.
(i)\(e^{jk\theta}\) representa (o códigos). \(\cos k\theta\). La parte real de la secuencia\(e^{jk\theta}\) es la secuencia cosinusoidal\(\cos k\theta\):
\[\operatorname{Re}\left[e^{j k \theta}\right]=\cos k \theta \nonumber \]
Por lo tanto, el fasor de tiempo discreto\(e^{jk\theta}\) representa (o códigos)\(\cos k\theta\) de la misma manera que los\(e^{j \omega t}\) códigos de fasor de tiempo continuo\(\cos \omega t\). Si el filtro de media móvil
\[x_{n}=\sum_{k=0}^{\infty} h_{k} u_{n-k} \nonumber \]
tiene coeficientes reales, podemos obtener la respuesta a una secuencia cosinusoidal tomando la parte real de la siguiente suma:
\ [\ begin {align}
x_ {n} &=\ sum_ {k=0} ^ {\ infty} h_ {k}\ cos (n-k)\ theta\ nonumber\\
&=\ nombreoperador {Re}\ izquierda [\ sum_ {k=0} ^ {\ infty} h_ {k} e^ {j (n-k)\ theta}\ derecha]\ nonumber\\
&=\ nombreoperador {Re}\ izquierda [e^ {j n\ theta}\ suma_ {k=0} ^ {\ infty} h_ {k} e^ {-j k\ theta}\ derecha ]
\ end {align}\ nonumber\]
En esta fórmula, la suma
\(\sum_{k=0}^{\infty} h_{k} e^{-j k \theta}\)
se llama la respuesta de frecuencia compleja del filtro y se le da el símbolo
\[H\left(e^{j \theta}\right)=\sum_{k=0}^{\infty} h_{k} e^{-j k \theta} \nonumber \]
Esta respuesta de frecuencia compleja es solo un número complejo, con una magnitud\(\left|H\left(e^{j \theta}\right)\right|\) y una fase arg\(H\left(e^{j \theta}\right)\). Por lo tanto, la salida del filtro de media móvil es
\ [\ begin {align}
x_ {n} &=\ qquad\ quad\ quad\ nombreoperador {Re}\ izquierda [e^ {j n\ theta} H\ izquierda (e^ {j\ theta}\ derecha)\ derecha]\ nonumber\\
&=\ quad\ nombreoperador {Re}\ izquierda [e^ {j n\ theta}\ izquierda|h\ izquierda (e^ ^ {j\ theta}\ derecha)\ derecha| e^ {\ arg H\ izquierda (e^ {j\ theta}\ derecha)}\ derecha]\ nonumber\\
&=\ izquierda|H\ izquierda (e^ {j\ theta}\ derecha)\ derecha|\ cos\ izquierda [n\ theta+\ arg H\ izquierda (e^ {j\ theta}\ derecha)\ derecha]
\ end {align}\ nonumber\]
Este notable resultado dice que la salida también es cosinusoidal, pero su amplitud es\(\left|H\left(e^{j \theta}\right)\right|\) más que 1, y su fase es\(argH\left(e^{j \theta}\right)\) más que 0. En los ejemplos a seguir, mostraremos que la compleja “ganancia”\(H\left(e^{j \theta}\right)\) puede ser altamente selectiva en\(\theta\), lo que significa que los cosenos de algunas frecuencias angulares se pasan con poca atenuación mientras que los cosenos de otras frecuencias se atenúan dramáticamente. Al elegir los coeficientes de filtro, podemos diseñar la selectividad de frecuencia que nos gustaría tener.
(ii)\(e^{jk\theta}\) es una versión de datos muestreados de\(e^{j\omega t}\). El fasor de tiempo discreto\(e^{jk\theta}\) puede producirse físicamente muestreando el fasor de tiempo continuo\(e^{j\omega t}\) en los instantes de muestreo periódicos\(t_k=kT\):
\ [\ begin {reunió}
e^ {j k\ theta} =\ izquierda.e^ {j\ omega t}\ derecha|_ {t=k T} =e^ {j\ omega k T}
\\ theta=\ omega T.
\ end {reunido}\ nonumber\]
Las dimensiones de\(\theta\) son radianes, las dimensiones de\(\omega\) son radianes/segundo, y las dimensiones de\(T\) son segundos. Llamamos\(T\) el intervalo de muestreo y\(\frac{1}{T}\) la frecuencia de muestreo o frecuencia de muestreo. Si la frecuencia angular original del fasor\(e^{j\omega t}\) se incrementa a\(\omega+m\left(\frac{2 \pi}{T}\right)\), entonces el fasor de tiempo discreto permanece\(e^{jk\theta}\):
\[\left.e^{j[\omega+m(2 \pi / T)] t}\right|_{t=k T}=e^{j(\omega k T+k m 2 \pi)}=e^{j k \theta} \nonumber \]
Esto significa que todos los fasores de tiempo continuo de la forma\(e^{j[\omega+m(2 \pi / T)] t}\) “se esconden bajo el mismo alias” cuando se ven a través de la operación de muestreo. Es decir, el fasor de datos muestreados no puede distinguir la frecuencia\(\omega\) de la frecuencia\(\omega+m \frac{2 \pi}{T}\). En sus cursos posteriores estudiará el aliasing con más detalle y estudiará la regla Nyquist para el muestreo:
\ [T\ leq\ frac {2\ pi} {\ Omega};\ quad\ frac {1} {T}\ geq\ frac {\ Omega} {2\ pi}]
Esta regla dice que se deben muestrear señales a una velocidad\(\left(\frac{1}{T}\right)\) que exceda el ancho\(\frac{\Omega}{2 \pi}\) de banda de la señal.
Pasemos la secuencia cosinusoidal\(u_{k}=\cos k \theta\) a través del filtro de promedio móvil finito
\ [\ comenzar {reunido}
x_ {n} =\ suma_ {k=0} ^ {N-1} h_ {k} u_ {n-k}\\
h_ {k} =\ frac {1} {N} k=0,1,\ lpuntos, N-1
\ final {reunido}\ nonumber\]
Sabemos por nuestro resultado anterior que la salida es
\[x_{n}=\left|H\left(e^{j \theta}\right)\right| \cos \left[n \theta+\arg H\left(e^{j \theta}\right)\right] . \nonumber \]
La respuesta de frecuencia compleja para este ejemplo es
\ [\ begin {align}
H\ left (e^ {j\ theta}\ derecha) &=\ sum_ {k=0} ^ {N-1}\ frac {1} {N} e^ {-j k\ theta}\ nonumber\\
&=\ frac {1} {N}\ frac {1-e^ {-j M\ theta}} {1-e^ {-j\ theta}}
\ end {align}\ nonumber\]
(¿Ves a tu viejo amigo, la fórmula de suma finita, en el trabajo?) Tratemos de manipular el resultado en una forma más elegante:
\ [\ begin {align}
H\ izquierda (e^ {j\ theta}\ derecha) &=\ frac {1} {N}\ frac {e^ {-j (N/2)\ theta}\ izquierda [e^ {j (N/2)\ theta} -e^ {-j (N/2)\ theta}\ derecha]} {e^ {-j (\ theta/2)}\ izquierda [e^ {(\ theta 2)} -e^ {-j (\ theta 2)}\ derecha]}\ nonumber\\
&=\ frac {1} {N} e^ {-j [(N-1)/2]\ theta}\ frac {\ sin\ left (\ frac {N} {2}\ theta\ derecha)} {\ sin\ izquierda (\ frac {1} {2}\ theta\ derecha)}.
\ end {align}\ nonumber\]
La magnitud de la función\(H(e^{j\theta})\) es
\[\left|H\left(e^{j \theta}\right)\right|=\frac{1}{N},\left|\frac{\sin \left(\frac{N}{2} \theta\right)}{\sin \left(\frac{1}{2} \theta\right)}\right| . \nonumber \]
At\(\theta=0\), correspondiente a un “fasor DC”,\(H(e^{j\theta})\) es igual a 1; at\(\theta=\frac{2 \pi}{N}\left|H\left(e^{j \theta}\right)=0\right|\). La magnitud de la respuesta de frecuencia compleja se grafica en la Figura 4.
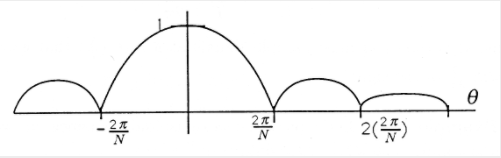
Este resultado muestra que el filtro de promedio móvil es selectivo en frecuencia, pasando frecuencias bajas con ganancia cercana a 1 y frecuencias altas con ganancia cercana a 0.
Calcular la fase de la respuesta de frecuencia compleja
\(H\left(e^{j \theta}\right)=\frac{1}{N} e^{-j[(N-1) / 2] \theta} \frac{\sin \left(\frac{N}{2} \theta\right)}{\sin \left(\frac{1}{2} \theta\right)}\)
Elija la longitud del filtro\(N\) para\(h_{k}=\frac{1}{N}, k=0,1, \ldots, N-1\) que un coseno de 60 Hz, muestreado a la velocidad\(\frac{1}{T} = 180\), quede perfectamente puesto a cero a medida que pasa por el filtro.
(MATLAB) Escribe un programa MATLAB para calcular y trazar la magnitud\(\left|H\left(e^{j \theta}\right)\right|\) y la fase arg\(H\left(e^{j \theta}\right)\) versus\(-\pi < \theta < \pi\) when
\(H\left(e^{j \theta}\right)=\frac{1}{N} e^{-j[(N-1) / 2] \theta} \frac{\sin \left(\frac{N}{2} \theta\right)}{\sin \left(\frac{1}{2} \theta\right)}\)
Elija incrementos adecuados para\(\theta\).
Calcular la respuesta de frecuencia compleja\(H\left(e^{j \theta}\right)\) para el filtro recursivo\(x_{n}=a x_{n-1}+w_{0} u_{n}\).