7.3: De símbolos a códigos binarios
- Page ID
- 82315
Quizás la idea más fundamental en la teoría de la comunicación es que los símbolos arbitrarios pueden ser representados por cadenas de dígitos binarios. Estas cadenas se llaman palabras binarias, direcciones binarias o códigos binarios. En los casos más simples, un alfabeto finito que consiste en las letras o símbolos\(s_{0}, s_{1}, \ldots, s_{M-1}\) está representado por códigos binarios. La forma obvia de implementar la representación es dejar que el código\(i^{\text {th }}\) binario sea la representación binaria para el subíndice\(i\):
\ [\ begin {reunió}
s_ {0}\ sim 000=a_ {0}\\
s_ {1}\ sim 001=a_ {1}\
\\ vdots\\
s_ {6}\ sim 110=a_ {6}\
s_ {7}\ sim 111=a_ {7}.
\ end {reunido}\ nonumber\]
El número de bits requeridos para el código binario es\(N\) donde
\[2^{N-1}<M \leq 2^{N} \nonumber \]
Decimos, más o menos, eso\(N=\log _{2} M\).
Códigos Octales
Cuando el número de símbolos es grande y los códigos binarios correspondientes contienen muchos bits, entonces normalmente agrupamos los bits en grupos de tres y reemplazamos el código binario por su código octal correspondiente. Por ejemplo, un código binario de siete bits se mapea en un código octal de tres dígitos de la siguiente manera:
\ [\ comenzar {reunido}
0000000\ sim 000\\
0000001\ sim 001\
\\ vdots\\
0100110\ sim 046\
\ vdots\\
101111\ sim 137\
\ vdots\\
1111111\ sim 177.
\ end {reunido}\ nonumber\]
Los códigos ASCII octales para representar letras, números y caracteres especiales se tabulan en la Tabla 1.
Escriba los códigos ASCII de siete bits para\(A,q,7\), y {.
| '0 | '1 | '2 | '3 | '4 | '5 | '6 | '7 | |
| '00x | ␀ | ␁ | ␂ | ␃ | ␄ | ␅ | ␆ | ␇ |
| '01x | ␈ | ␉ | ␊ | ␋ | ␌ | ␍ | ␎ | ␏ |
| '02x | ␐ | ␑ | ␒ | ␓ | ␔ | ␕ | ␖ | ␗ |
| '03x | ␘ | ␙ | ␚ | ␛ | ␜ | ␝ | ### | ␟ |
| '04x | ␠ | ! | “ | # | $ | % | & | ' |
| '05x | ( | ) | * | + | , | - | . | / |
| '06x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| '07x | 8 | 9 | : | ; | < | = | > | ? |
| '10x | @ | A | B | C | D | E | F | G |
| '11x | H | I | J | K | L | M | N | O |
| '12x | P | Q | R | S | T | U | V | W |
| '13x | X | Y | Z | [ | \ | ] | ^ | _ |
| '14x | ` | a | b | c | d | e | f | g |
| '15x | h | i | j | k | l | m | n | o |
| '16x | p | q | r | s | t | u | v | w |
| '17x | x | y | z | { | | | } | ~ | ␡ |
Agregue un 1 o un 0 a la posición más significativa (más a la izquierda) del código ASCII de siete bits para producir un código de ocho bits que tenga paridad par (número par de 1). Dé los códigos ASCII de ocho bits resultantes y los correspondientes códigos octales de tres dígitos para%, u, f, 8 y +.
Cuantificadores y Convertidores A/D
¿Y si el alfabeto fuente es infinito? Nuestra única esperanza es aproximarlo con una colección finita de palabras binarias finitas. Por ejemplo, supongamos que la salida de la fuente es una tensión analógica que se encuentra entre\(−V_0\) y\(+V_0\). Podríamos romper este rango pico a pico en pequeñas celdas de voltaje de tamaño\(\frac{2V}{M} A\) y aproximar el voltaje en cada celda por su punto medio. Este esquema se ilustra en la Figura 1. En la figura, la celda\(C_i\) se define como el conjunto de voltajes que caen entre\(i_{M^{-} \overline{M}}^{\underline{2} V p V_{\Delta}}\) y\(i^{\underline{2} V} M \Delta+\stackrel{V}{-} M^{\mathrm{A}}\):
\[C_{i}=\left\{V: i . \frac{2 V_{0}}{M}-\frac{V_{0}}{M}<V \leq i \frac{2 V_{0}}{M}+\frac{V_{0}}{M}\right\} \nonumber \]
El mapeo de valores continuos de\(V\) a un conjunto finito de aproximaciones es
\[Q(V)=i \frac{2 V_{0}}{M}, \text { if } V \in C_{i} \nonumber \]
Es decir,\(V\) se sustituye por la aproximación cuantificada\(i_{M}^{\underline{2} V_{0}}\) siempre que\(V\) se encuentre en celda\(C_i\). Podemos representar los valores cuantificados\(i_{M}^{\underline{2} V_{0}}\) con códigos binarios simplemente representando el subíndice de la celda por una palabra binaria. En un curso posterior sobre electrónica digital y microprocesadores estudiarás convertidores A/D (analógico a digital) para cuantificar variables.
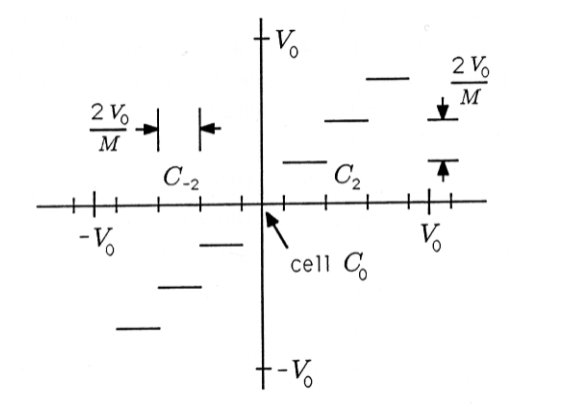
Si\(M=8\), correspondiente a un cuantificador de tres bits, podemos asociar celdas cuantificadoras y niveles cuantificados con códigos binarios de la siguiente manera:
\ (\ begin {array} {ll}
V\ en C_ {-3} &\ Rightarrow V_ {-3} =( -3)\ frac {2 V_ {0}} {8}\ sim 111\\
V\ en C_ {-2} &\ Rightarrow V_ {-2} =( -2)\ frac {2 V_ {0}} {8}\ sim 110\
V\ en C_ {-1} &\ Rightarrow V_ {-1} =( -1)\ frac {2 V_ {0}} {8}\ sim 101\\
V\ en C_ {0} & amp;\ Rightarrow\ quad V_ {0} =0\ sim 000\\
V\ en C_ {1} &\ Rightarrow V_ {1} =( 1)\ frac {2 V_ {0}} {8}\ sim 001\\
V\ en C_ {2} &\ Rightarrow V_ {2} =( 2)\ frac {2 V_ {0} {8}\ sim 010\\
V\ en C_ {3} &\ Rightarrow V_ {3} =( 3)\ frac {2 V_ {0}} {8}\ sim 011.
\ end {array}\)
Este código particular se denomina código de signo-magnitud, en el que el bit más significativo es un bit de signo y los bits restantes son bits de magnitud (por ejemplo,\(110 \sim−2\) y\(010 \sim 2\)). Uno de los defectos del código de signo-magnitud es que desperdicia un código al usar 000 para 0 y 100 para -O. Un código alternativo que tiene muchas otras ventajas es el código de complemento de los 2. Los códigos de complemento 2′spara números positivos son los mismos que los códigos de signo-magnitud, pero los códigos para números negativos se generan complementando todos los bits para el número positivo correspondiente y sumando 1:
\ (\ begin {alineado}
-4 &\ sim 100 &\\
-3 &\ sim 101 & (100+1)\\
-2 &\ sim 110 & (101+1)\\
-1 &\ sim 111 & (110+1)\\
0 &\ sim 000\\
1 &\ sim 001\\
2 &\ sim 010\\
3 &\ sim 011.
\ end {alineado}\)
Genere los códigos binarios complementarios de señal de cuatro bits y dos de cuatro bits para los números\(-8,-7, \ldots,-1,0,1,2, \ldots, 7\).
Demostrar que, en la representación complementaria de los 2, los códigos binarios para\(−n\) y\(+n\) suman a cero. Por ejemplo,
\ [\ begin {reunió}
101+011=000\\
(-3) (3) (0).
\ end {reunido}\ nonumber\]
En tus cursos de aritmética informática aprenderás a hacer aritmética en diversos sistemas codificados binarios. El siguiente problema ilustra lo fácil que es la aritmética en el complemento de 2.
Genera una tabla de sumas para todos los números de complemento de 2 entre −4 y +3. Demostrar que las sumas son correctas. Usa 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, y 1 + 1 = 0 con un acarreo en el siguiente bit. Por ejemplo, 001+001=010.
Árboles binarios y códigos de longitud variable
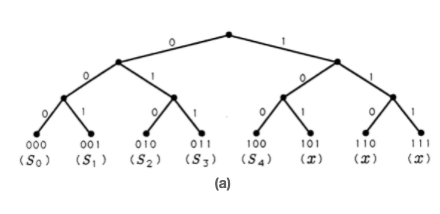
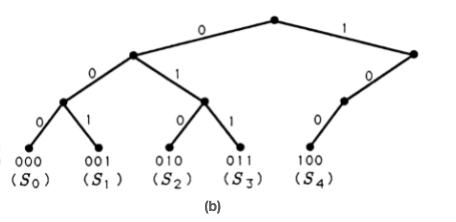
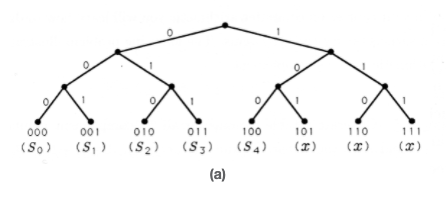
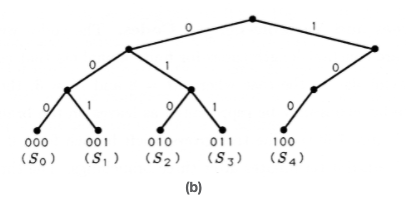
Los códigos que hemos construido hasta ahora son códigos de longitud constante para alfabetos finitos que contienen exactamente\(M=2^N\) símbolos. En el caso donde\(M=8\) y\(N=3\), entonces los ocho posibles códigos de tres bits pueden representarse como hojas en el árbol de ramificación ilustrado en la Figura 2 (a). El árbol crece una rama izquierda para un 0 y una rama derecha para un 1, hasta que termina después de tres ramificaciones. Los códigos de tres bits que hemos estudiado hasta ahora residen en las hojas terminadoras del árbol binario. Pero, ¿y si nuestro alfabeto fuente contiene solo cinco símbolos o letras? Podemos representar estos cinco símbolos como los símbolos de tres bits del 000 al 100 en el árbol binario. Esto genera un código de longitud constante con tres símbolos no utilizados, o ilegales, 101 a 111. Estos están marcados con un "\(x\)" en la Figura 2 (a). Estas hojas no utilizadas y las ramas que conducen a ellas pueden podarse para producir el árbol binario de la Figura 2 (b).
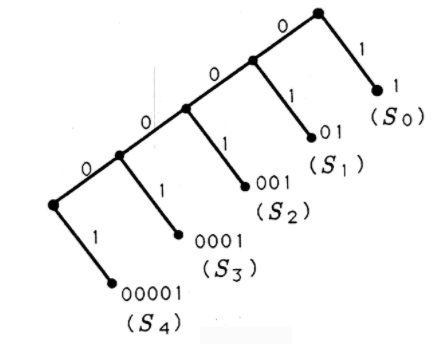
Si admitimos códigos de longitud variable, entonces tenemos varias otras opciones para usar un árbol binario para construir códigos binarios. Dos de estos códigos y sus correspondientes árboles binarios se ilustran en la Figura 3. Si nos desabusamos de la noción de que cada palabra de código debe contener tres o menos bits, entonces podemos construir árboles binarios como los de la Figura 4 y generar sus correspondientes códigos binarios. En la Figura 4 (a), cultivamos una rama derecha después de cada rama izquierda y etiquetamos cada hoja con una palabra clave. En la Figura 4 (b), podamos la última rama derecha y asociamos una palabra clave con la hoja en la última rama izquierda.
Todos los códigos que hemos generado hasta el momento están organizados en la Tabla 2. Para cada código, se tabula el número promedio de bits/símbolo. Este promedio oscila entre 2.4 y 3.0. Si es igualmente probable que aparezcan todos los símbolos, entonces el mejor código de longitud variable sería el código 2.
Todos los códigos que hemos construido tienen una característica común: cada palabra de código es una hoja de terminación en un árbol binario, lo que significa que ninguna palabra de código se encuentra a lo largo de una rama de ramas a otra palabra de código. Decimos que ninguna palabra clave es un prefijo a otra palabra clave. Esta propiedad hace que cada uno de los códigos sea decodificable instantáneamente, lo que significa que cada bit en una cadena de bits puede procesarse instantáneamente (o independientemente) sin depender de bits posteriores.
Decodifique la siguiente secuencia de bits usando el código 2:
01110011000000101100111.
 (a)
(a)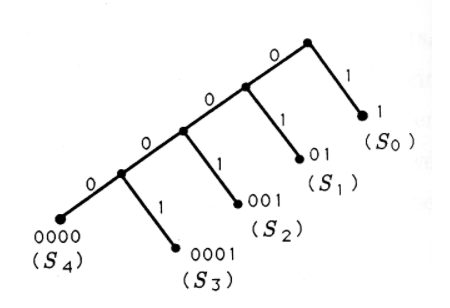
| Código # | S0S0 | S1S1 | S2S2 | S3S3 | S4S4 | Promedio de bits/símbolo |
|---|---|---|---|---|---|---|
| 1 | 000 | 001 | 010 | 011 | 100 | 15/5=3.015/5=3.0 |
| 2 | 000 | 001 | 01 | 10 | 11 | 12/5=2.412/5=2.4 |
| 3 | 000 | 001 | 010 | 011 | 1 | 13/5=2.613/5=2.6 |
| 4 | 1 | 01 | 001 | 0001 | 00001 | 15/5=3.015/5=3.0 |
| 5 | 1 | 01 | 001 | 0001 | 0000 | 14/5=2.8 |
Ilustrar los siguientes códigos en un árbol binario. ¿Cuáles de ellos son decodificables instantáneamente? ¿Cuáles se pueden podar y permanecer instantáneamente decodificables?
\ (\ begin {array} {ccccc}
S_ {0} & S_ {1} & S_ {2} & S_ {3} & S_ {4}\\
011 & 100 & 00 & 11 & 101\\
011 & 100 & 00 & 0 & 01\\
010 & 000 & 100 & 101 & 111.
\ end {array}\)
El código #2 generado en la Tabla 2 parece un mejor código que el código #5 porque su número promedio de bits/símbolo (2.4) es menor. Pero, ¿y si el símbolo\(S_0\) es un símbolo muy probable y el símbolo\(S_4\) es muy poco probable? Entonces bien puede resultar que el número promedio de bits utilizados por el código #5 es menor que el número promedio utilizado por el código #2. Entonces, ¿cuál es el mejor código? La respuesta depende de la frecuencia relativa de uso de cada símbolo. Exploramos esta pregunta en la siguiente sección.


