1.5: Capítulo 1 Ejercicios con Soluciones
- Page ID
- 110729
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En Ejercicios\(\PageIndex{1}\) -\(\PageIndex{8}\), encuentra la factorización prima del número natural dado.
Ejercicio\(\PageIndex{1}\)
80
- Contestar
-
\(80=2 \cdot 2 \cdot 2 \cdot 2 \cdot 5\)
Ejercicio\(\PageIndex{2}\)
108
Ejercicio\(\PageIndex{3}\)
180
- Contestar
-
\(180=2 \cdot 2 \cdot 3 \cdot 3 \cdot 5\)
Ejercicio\(\PageIndex{4}\)
160
Ejercicio\(\PageIndex{5}\)
128
- Contestar
-
\(128=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\)
Ejercicio\(\PageIndex{6}\)
192
Ejercicio\(\PageIndex{7}\)
32
- Contestar
-
\(32=2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\)
Ejercicio\(\PageIndex{8}\)
72
En Ejercicios\(\PageIndex{9}\) -\(\PageIndex{16}\), convierte el decimal dado a una fracción.
Ejercicio\(\PageIndex{9}\)
0.648
- Contestar
-
Hay tres decimales, entonces\(0.648=\frac{648}{1000}=\frac{81}{125}\)
Ejercicio\(\PageIndex{10}\)
0.62
Ejercicio\(\PageIndex{11}\)
0.240
- Contestar
-
Hay tres decimales, entonces\(0.240=\frac{240}{1000}=\frac{6}{25}\)
Ejercicio\(\PageIndex{12}\)
0.90
Ejercicio\(\PageIndex{13}\)
0.14
- Contestar
-
Hay dos decimales, entonces\(0.14=\frac{14}{100}=\frac{7}{50}\)
Ejercicio\(\PageIndex{14}\)
0.760
Ejercicio\(\PageIndex{15}\)
0.888
- Contestar
-
Hay tres decimales, entonces\(0.888=\frac{888}{1000}=\frac{111}{125}\)
Ejercicio\(\PageIndex{16}\)
0.104
En Ejercicios\(\PageIndex{17}\) -\(\PageIndex{24}\), convierta el decimal repetido dado a una fracción.
Ejercicio\(\PageIndex{17}\)
\(0 . \overline{27}\)
- Contestar
-
Vamos\(x=0 . \overline{27} .\) Entonces\(100 x=27 . \overline{27} .\) restando en ambos lados de estas ecuaciones.
\[\begin{aligned} 100 x &=27 . \overline{27} \\ x &=0 . \overline{27} \end{aligned}\]
rendimientos\(99 x=27 .\) Por último, resolver\(x\) por dividiendo por\(99 : x=\frac{27}{99}=\frac{3}{11}\).
Ejercicio\(\PageIndex{18}\)
\(0 . \overline{171}\)
Ejercicio\(\PageIndex{19}\)
\(0 . \overline{24}\)
- Contestar
-
Let\(x=0 . \overline{24} .\)\(100 x=24 . \overline{24} .\) Then restando en ambos lados de estas ecuaciones\[\begin{aligned} 100 x &=24 . \overline{24} \\ x &=0 . \overline{24} \end{aligned}\]
rendimientos\(99 x=24 .\) Por último, resolver\(x\) dividiendo por\(99 : x=\frac{24}{99}=\frac{8}{33}\)
Ejercicio\(\PageIndex{20}\)
\(0 . \overline{882}\)
Ejercicio\(\PageIndex{21}\)
\(0 . \overline{84}\)
- Contestar
-
Let\(x=0 . \overline{84} .\)\(100 x=84 . \overline{84} .\) Then restando en ambos lados de estas ecuaciones
\[\begin{aligned} 100 x &=84 . \overline{.84} \\ x &=0 . \overline{84} \end{aligned}\]
rendimientos\(99 x=84 .\) Por último, resolver\(x\) dividiendo por\(99 : x=\frac{84}{99}=\frac{28}{33}\)
Ejercicio\(\PageIndex{22}\)
\(0 . \overline{384}\)
Ejercicio\(\PageIndex{23}\)
\(0 . \overline{63}\)
- Contestar
-
Let\(x=0 . \overline{63} .\)\(100 x=63 . \overline{63} .\) Then restando en ambos lados de estas ecuaciones
\[\begin{aligned} 100 x &=63 . \overline{63} \\ x &=0 . \overline{63} \end{aligned}\]
rendimientos\(99 x=63 .\) Por último, resolver\(x\) dividiendo por\(99 : x=\frac{63}{99}=\frac{7}{11}\)
Ejercicio\(\PageIndex{24}\)
\(0 . \overline{60}\)
Ejercicio\(\PageIndex{25}\)
Demostrar que\(\sqrt{3}\) es irracional.
- Contestar
-
Supongamos que eso\(\sqrt{3}\) es racional. Entonces se puede expresar como la relación de dos enteros p y q de la siguiente manera:
\[\sqrt{3}=\frac{p}{q}\]
Cuadrado ambos lados,\[3=\frac{p^{2}}{q^{2}}\]
luego borre la ecuación de fracciones multiplicando ambos lados por\(q^{2}\):
\[p^{2}=3 q^{2}\]
Ahora p y q cada uno tiene sus propias factorizaciones prime únicas. Ambos\(p^{2}\) y\(q^{2}\) tienen un número par de factores en sus factorizaciones prime. Pero esto contradice la ecuación (1), porque el lado izquierdo tendría un número par de factores en su factorización prima, mientras que el lado derecho tendría un número impar de factores en su factorización primo (hay un 3 extra en el lado derecho).
Por lo tanto, nuestra suposición de que\(\sqrt{3}\) era racional es falsa. Así,\(\sqrt{3}\) es irracional.
Ejercicio\(\PageIndex{26}\)
Demostrar que\(\sqrt{5}\) es irracional.
En Ejercicios\(\PageIndex{27}\) -\(\PageIndex{30}\), copia la tabla dada en tu papel de tarea. En cada fila, coloque una marca de verificación en cada columna que sea apropiada. Es decir, si el número al inicio de la fila es racional, coloque una marca de verificación en la columna racional. Nota: La mayoría de las filas (pero no todas) tendrán más de una marca de verificación.
Ejercicio\(\PageIndex{27}\)
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| 0 | |||||
| -2 | |||||
| -2/3 | |||||
| 0.15 | |||||
| \(0 . \overline{2}\) | |||||
| \(\sqrt{5}\) |
- Contestar
-
\(\mathbb{N}\) \(\mathbb{W}\) \(\mathbb{Z}\) \(\mathbb{Q}\) \(\mathbb{R}\) 0 x x x x -2 x x x -2/3 x x 0.15 x x \(0 . \overline{2}\) x x \(\sqrt{5}\) x
Ejercicio\(\PageIndex{28}\)
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| 10/2 | |||||
| \(\pi\) | |||||
| -6 | |||||
| \(0 . \overline{9}\) | |||||
| \(\sqrt{2}\) | |||||
| 0.37 |
Ejercicio\(\PageIndex{29}\)
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| -4/3 | |||||
| 12 | |||||
| 0 | |||||
| \(\sqrt{11}\) | |||||
| \(1. \overline{3}\) | |||||
| 6/2 |
- Contestar
-
\(\mathbb{N}\) \(\mathbb{W}\) \(\mathbb{Z}\) \(\mathbb{Q}\) \(\mathbb{R}\) -4/3 x x 12 x x x x x 0 x x x x \(\sqrt{11}\) x \(1. \overline{3}\) x x 6/2 x x x x x
Ejercicio\(\PageIndex{30}\)
| \(\mathbb{N}\) | \(\mathbb{W}\) | \(\mathbb{Z}\) | \(\mathbb{Q}\) | \(\mathbb{R}\) | |
| -3/5 | |||||
| \(\sqrt{10}\) | |||||
| 1.625 | |||||
| 10/2 | |||||
| 0/5 | |||||
| 11 |
En Ejercicios\(\PageIndex{31}\) -\(\PageIndex{42}\), considere la afirmación dada y determine si es verdadera o falsa. Escribe una frase explicando tu respuesta. En particular, si la declaración es falsa, trate de dar un ejemplo que contradiga la afirmación.
Ejercicio\(\PageIndex{31}\)
Todos los números naturales son números enteros.
- Contestar
-
Cierto. La única diferencia entre los dos conjuntos es que el conjunto de números enteros contiene el número 0.
Ejercicio\(\PageIndex{32}\)
Todos los números enteros son números racionales.
Ejercicio\(\PageIndex{33}\)
Todos los números racionales son enteros.
- Contestar
-
Falso. Por ejemplo, no\(\frac{1}{2}\) es un entero.
Ejercicio\(\PageIndex{34}\)
Todos los números racionales son números enteros.
Ejercicio\(\PageIndex{35}\)
Algunos números naturales son irracionales.
- Contestar
-
Falso. Todos los números naturales son racionales, y por lo tanto no irracionales.
Ejercicio\(\PageIndex{36}\)
Algunos números enteros son irracionales.
Ejercicio\(\PageIndex{37}\)
Algunos números reales son irracionales.
- Contestar
-
Cierto. Por ejemplo, π y √2 son números reales que son irracionales.
Ejercicio\(\PageIndex{38}\)
Todos los enteros son números reales.
Ejercicio\(\PageIndex{39}\)
Todos los enteros son números racionales.
- Contestar
-
Cierto. Cada entero b se puede escribir como una fracción b/1.
Ejercicio\(\PageIndex{40}\)
No hay números racionales son números naturales.
Ejercicio\(\PageIndex{41}\)
No hay números reales son enteros.
- Contestar
-
Falso. Por ejemplo, 2 es un número real que también es un número entero.
Ejercicio\(\PageIndex{42}\)
Todos los números enteros son números naturales.
En Ejercicios\(\PageIndex{43}\) -\(\PageIndex{54}\), resuelve cada una de las ecuaciones dadas para x.
Ejercicio\(\PageIndex{43}\)
45x + 12 = 0
- Contestar
-
\[\begin{aligned} & 45 x+12=0 \\ \Longrightarrow \quad & 45 x=-12 \\ \Longrightarrow \quad& x=-\frac{12}{45}=-\frac{4}{15} \end{aligned}\]
Ejercicio\(\PageIndex{44}\)
76x − 55 = 0
Ejercicio\(\PageIndex{45}\)
x − 7 = −6x + 4
- Contestar
-
\[\begin{aligned} & x-7=-6 x+4 \\ \Longrightarrow \quad & x+6 x=4+7 \\ \Longrightarrow \quad & 7 x=11 \\ \Longrightarrow \quad & x=\frac{11}{7} \end{aligned}\]
Ejercicio\(\PageIndex{46}\)
−26x + 84 = 48
Ejercicio\(\PageIndex{47}\)
37x + 39 = 0
- Contestar
-
\[\begin{aligned} & 37 x+39=0 \\ \Longrightarrow\quad & 37 x=-39 \\ \Longrightarrow\quad & x=-\frac{39}{37} \end{aligned}\]
Ejercicio\(\PageIndex{48}\)
−48x + 95 = 0
Ejercicio\(\PageIndex{49}\)
74x − 6 = 91
- Contestar
-
\[\begin{aligned} & 74 x-6=91 \\ \Longrightarrow\quad & 74 x=97 \\ \Longrightarrow\quad & x=\frac{97}{74} \end{aligned}\]
Ejercicio\(\PageIndex{50}\)
−7x + 4 = −6
Ejercicio\(\PageIndex{51}\)
−88x + 13 = −21
- Contestar
-
\[\begin{aligned} &-88 x+13=-21 \\ \Longrightarrow\quad &-88 x=-34 \\ \Longrightarrow \quad & x=\frac{-34}{-88}=\frac{17}{44} \end{aligned}\]
Ejercicio\(\PageIndex{52}\)
−14x − 81 = 0
Ejercicio\(\PageIndex{53}\)
19x + 35 = 10
- Contestar
-
\[\begin{aligned} & 19 x+35=10 \\ \Longrightarrow\quad & 19 x=-25 \\ \Longrightarrow\quad & x=-\frac{25}{19} \end{aligned}\]
Ejercicio\(\PageIndex{54}\)
−2x + 3 = −5x − 2
En Ejercicios\(\PageIndex{55}\) -\(\PageIndex{66}\), resuelve cada una de las ecuaciones dadas para x.
Ejercicio\(\PageIndex{55}\)
6 − 3 (x + 1) = −4 (x + 6) + 2
- Contestar
-
\[\begin{aligned} & 6-3(x+1)=-4(x+6)+2 \\ \Longrightarrow\quad & 6-3 x-3=-4 x-24+2 \\ \Longrightarrow\quad &-3 x+3=-4 x-22 \\ \Longrightarrow\quad &-3 x+4 x=-22-3 \\ \Longrightarrow\quad & x=-25 \end{aligned}\]
Ejercicio\(\PageIndex{56}\)
(8x + 3) − (2x + 6) = −5x + 8
Ejercicio\(\PageIndex{57}\)
−7 − (5x − 3) = 4 (7x + 2)
\[\begin{aligned} &-7-(5 x-3)=4(7 x+2) \\ \Longrightarrow\quad &-7-5 x+3=28 x+8 \\ \Longrightarrow\quad &-5 x-4=28 x+8 \\ \Longrightarrow\quad &-5 x-28 x=8+4 \\ \Longrightarrow\quad &-33 x=12 \\ \Longrightarrow\quad & x=-\frac{12}{33}=-\frac{4}{11} \end{aligned}\]
Ejercicio\(\PageIndex{58}\)
−3 − 4 (x + 1) = 2 (x + 4) + 8
Ejercicio\(\PageIndex{59}\)
9 − (6x − 8) = −8 (6x − 8)
- Contestar
-
\[\begin{aligned} & 9-(6 x-8)=-8(6 x-8) \\ \Longrightarrow \quad & 9-6 x+8=-48 x+64 \\ \Longrightarrow\quad &-6 x+17=-48 x+64 \\ \Longrightarrow\quad &-6 x+48 x=64-17 \\ \Longrightarrow\quad & 42 x=47 \\ \Longrightarrow\quad & x=\frac{47}{42} \end{aligned}\]
Ejercicio\(\PageIndex{60}\)
−9 − (7x − 9) = −2 (−3x + 1)
Ejercicio\(\PageIndex{61}\)
(3x − 1) − (7x − 9) = −2x − 6
- Contestar
-
\[\begin{aligned} &(3 x-1)-(7 x-9)=-2 x-6 \\ \Longrightarrow\quad & 3 x-1-7 x+9=-2 x-6 \\ \Longrightarrow\quad &-4 x+8=-2 x-6 \\ \Longrightarrow\quad &-4 x+2 x=-6-8 \\ \Longrightarrow\quad &-2 x=-14 \\ \Longrightarrow\quad & x=7 \end{aligned}\]
Ejercicio\(\PageIndex{62}\)
−8 − 8 (x − 3) = 5 (x + 9) + 7
Ejercicio\(\PageIndex{63}\)
(7x − 9) − (9x + 4) = −3x + 2
- Contestar
-
\[\begin{aligned} &(7 x-9)-(9 x+4)=-3 x+2 \\ \Longrightarrow\quad & 7 x-9-9 x-4=-3 x+2 \\ \Longrightarrow\quad &-2 x-13=-3 x+2 \\ \Longrightarrow\quad &-2 x+3 x=2+13 \\ \Longrightarrow\quad & x=15 \end{aligned}\]
Ejercicio\(\PageIndex{64}\)
(−4x − 6) + (−9x + 5) = 0
Ejercicio\(\PageIndex{65}\)
−5 − (9x + 4) = 8 (−7x − 7)
- Contestar
-
\[\begin{array}{ll}{} & {-5-(9 x+4)=8(-7 x-7)} \\ {\Longrightarrow} & {-5-9 x-4=-56 x-56} \\ {\Longrightarrow} & {-9 x-9=-56 x-56} \\ {\Longrightarrow} & {-9 x+56 x=-56+9} \\ {\Longrightarrow} & {47 x=-47} \\ {\Longrightarrow} & {x=-1}\end{array}\]
Ejercicio\(\PageIndex{66}\)
(8x − 3) + (−3x + 9) = −4x − 7
En Ejercicios\(\PageIndex{67}\) -\(\PageIndex{78}\), resuelve cada una de las ecuaciones dadas para x. Consulta tus soluciones usando tu calculadora.
Ejercicio\(\PageIndex{67}\)
−3.7x − 1 = 8.2x − 5
- Contestar
-
Primero borra los decimales multiplicando por 10.
\[\begin{aligned} &-3.7 x-1=8.2 x-5 \\ \Longrightarrow\quad &-37 x-10=82 x-50 \\ \Longrightarrow\quad &-37 x-82 x=-50+10 \\ \Longrightarrow\quad &-119 x=-40 \\ \Longrightarrow\quad & x=\frac{40}{119} \end{aligned}\]
Aquí hay una comprobación de las soluciones en la calculadora gráfica. El lado izquierdo de la ecuación se evalúa en la solución en (a), el lado derecho de la ecuación se evalúa en la solución en (b). Tenga en cuenta que coinciden.

Ejercicio\(\PageIndex{68}\)
8.48x − 2.6 = −7.17x − 7.1
Ejercicio\(\PageIndex{69}\)
\(-\frac{2}{3} x+8=\frac{4}{5} x+4\)
- Contestar
-
Primeras fracciones claras multiplicando por 15.
\[\begin{aligned} &-\frac{2}{3} x+8=\frac{4}{5} x+4 \\ \Longrightarrow\quad &-10 x+120=12 x+60 \\ \Longrightarrow\quad &-10 x-12 x=60-120 \\ \Longrightarrow\quad &-22 x=-60 \\ \Longrightarrow\quad & x=\frac{-60}{-22}=\frac{30}{11} \end{aligned}\]
Aquí hay una comprobación de las soluciones en la calculadora gráfica. El lado izquierdo de la ecuación se evalúa en la solución en (a), el lado derecho de la ecuación se evalúa en la solución en (b). Tenga en cuenta que coinciden.

Ejercicio\(\PageIndex{70}\)
−8.4x = −4.8x + 2
Ejercicio\(\PageIndex{71}\)
\(-\frac{3}{2} x+9=\frac{1}{4} x+7\)
- Contestar
-
Primeras fracciones claras multiplicando por 4.
\[\begin{aligned} &-\frac{3}{2} x+9=\frac{1}{4} x+7 \\ \Longrightarrow\quad &-6 x+36=x+28 \\ \Longrightarrow\quad &-6 x-x=28-36 \\ \Longrightarrow\quad &-7 x=-8 \\ \Longrightarrow\quad & x=\frac{8}{7} \end{aligned}\]
Aquí hay una comprobación de las soluciones en la calculadora gráfica. El lado izquierdo de la ecuación se evalúa en la solución en (a), el lado derecho de la ecuación se evalúa en la solución en (b). Tenga en cuenta que coinciden.

Ejercicio\(\PageIndex{72}\)
2.9x − 4 = 0.3x − 8
Ejercicio\(\PageIndex{73}\)
5.45x + 4.4 = 1.12x + 1.6
- Contestar
-
Primero despeja los decimales multiplicando por 100.
\[\begin{aligned} & 5.45 x+4.4=1.12 x+1.6 \\ \Longrightarrow\quad & 545 x+440=112 x+160 \\ \Longrightarrow\quad & 545 x-112 x=160-440 \\ \Longrightarrow\quad & 433 x=-280 \\ \Longrightarrow\quad & x=-\frac{280}{433} \end{aligned}\]
Aquí hay una comprobación de las soluciones en la calculadora gráfica. El lado izquierdo de la ecuación se evalúa en la solución en (a), el lado derecho de la ecuación se evalúa en la solución en (b). Tenga en cuenta que coinciden.

Ejercicio\(\PageIndex{74}\)
\(-\frac{1}{4} x+5=-\frac{4}{5} x-4\)
Ejercicio\(\PageIndex{75}\)
\(-\frac{3}{2} x-8=\frac{2}{5} x-2\)
- Contestar
-
Primeras fracciones claras multiplicando por 10. \[\begin{aligned} &-\frac{3}{2} x-8=\frac{2}{5} x-2 \\ \Longrightarrow\quad &-15 x-80=4 x-20 \\ \Longrightarrow\quad &-15 x-4 x=-20+80 \\ \Longrightarrow\quad &-19 x=60 \\ \Longrightarrow\quad & x=-\frac{60}{19} \end{aligned}\]
Aquí hay una comprobación de las soluciones en la calculadora gráfica. El lado izquierdo de la ecuación se evalúa en la solución en (a), el lado derecho de la ecuación se evalúa en la solución en (b). Tenga en cuenta que coinciden.

Ejercicio\(\PageIndex{76}\)
\(-\frac{4}{3} x-8=-\frac{1}{4} x+5\)
Ejercicio\(\PageIndex{77}\)
−4.34x − 5.3 = 5.45x − 8.1
- Contestar
-
Primero despeja los decimales multiplicando por 100.
\[\begin{aligned} &-4.34 x-5.3=5.45 x-8.1 \\ \Longrightarrow\quad &-434 x-530=545 x-810 \\ \Longrightarrow\quad &-434 x-545 x=-810+530 \\ \Longrightarrow\quad &-979 x=-280 \\ \Longrightarrow\quad & x=\frac{280}{979} \end{aligned}\]
Aquí hay una comprobación de las soluciones en la calculadora gráfica. El lado izquierdo de la ecuación se evalúa en la solución en (a), el lado derecho de la ecuación se evalúa en la solución en (b). Tenga en cuenta que coinciden.

Ejercicio\(\PageIndex{78}\)
\(\frac{2}{3} x-3=-\frac{1}{4} x-1\)
En Ejercicios\(\PageIndex{79}\) -50, resuelve cada una de las ecuaciones dadas para la variable indicada.
Ejercicio\(\PageIndex{79}\)
P = IRT para R
- Contestar
-
\[\begin{aligned} & P=I R T \\ \Longrightarrow\quad & P=(I T) R \\ \Longrightarrow\quad & \frac{P}{I T}=\frac{(I T) R}{I T} \\ \Longrightarrow\quad & \frac{P}{I T}=R \end{aligned}\]
Ejercicio\(\PageIndex{80}\)
d = vt para t
Ejercicio\(\PageIndex{81}\)
\(v=v_{0}+a t\)para\(a\)
- Contestar
-
\[\begin{aligned} & v=v_{0}+a t \\ \Longrightarrow\quad & v-v_{0}=a t \\ \Longrightarrow\quad & \frac{v-v_{0}}{t}=a \end{aligned}\]
Ejercicio\(\PageIndex{82}\)
\(x=v_{0}+v t\)para\(v\)
Ejercicio\(\PageIndex{83}\)
Ax + Por = C para y
- Contestar
-
\[\begin{aligned} & A x+B y=C \\ \Longrightarrow\quad & B y=C-A x \\ \Longrightarrow\quad & y=\frac{C-A x}{B} \end{aligned}\]
Ejercicio\(\PageIndex{84}\)
y = mx + b para x
Ejercicio\(\PageIndex{85}\)
\(A=\pi r^{2}\)para\(\pi\)
- Contestar
-
\[\begin{aligned} A &=\pi r^{2} \\ \Longrightarrow \quad \frac{A}{r^{2}} &=\pi \end{aligned}\]
Ejercicio\(\PageIndex{86}\)
\(S=2 \pi r^{2}+2 \pi r h\)para\(h\)
Ejercicio\(\PageIndex{87}\)
\(F=\frac{k q q_{0}}{r^{2}}\)para\(k\)
- Contestar
-
\[\begin{aligned} & F=\frac{k q q_{0}}{r^{2}} \\ \Longrightarrow\quad & F r^{2}=k q q_{0} \\ \Longrightarrow\quad & \frac{F r^{2}}{q q_{0}}=k \end{aligned}\]
Ejercicio\(\PageIndex{88}\)
\(C=\frac{Q}{m T}\)para\(T\)
Ejercicio\(\PageIndex{89}\)
\(\frac{V}{t}=k\)para\(t\)
- Contestar
-
\[\begin{aligned} & \frac{V}{t}=k \\ \Longrightarrow\quad & V=k t \\ \Longrightarrow\quad & \frac{V}{k}=t \end{aligned}\]
Ejercicio\(\PageIndex{90}\)
\(\lambda=\frac{h}{m v}\)para\(v\)
Ejercicio\(\PageIndex{91}\)
\(\frac{P_{1} V_{1}}{n_{1} T_{1}}=\frac{P_{2} V_{2}}{n_{2} T_{2}}\)para\(V_{2}\)
- Contestar
-
Cruzar multiplicar, luego dividir por el coeficiente de\(V_{2}\).
\[\begin{aligned} & \frac{P_{1} V_{1}}{n_{1} T_{1}}=\frac{P_{2} V_{2}}{n_{2} T_{2}} \\ \Longrightarrow\quad & n_{2} P_{1} V_{1} T_{2}=n_{1} P_{2} V_{2} T_{1} \\ \Longrightarrow\quad & \frac{n_{2} P_{1} V_{1} T_{2}}{n_{1} P_{2} T_{1}}=V_{2} \end{aligned}\]
Ejercicio\(\PageIndex{92}\)
\(\pi=\frac{n R T}{V} i\)para\(n\)
Ejercicio\(\PageIndex{93}\)
Ata una pelota a una cuerda y gira alrededor en círculo con velocidad constante. Se sabe que la aceleración de la pelota es directamente hacia el centro del círculo y dada por la fórmula\[a=\frac{v^{2}}{r}\] donde a es aceleración, v es la velocidad de la pelota, y r es el radio del círculo de movimiento.
i. Resolver fórmula (1) para r.
ii. Dado que la aceleración de la bola es de 12 m/s2 y la velocidad es de 8 m/s, encuentra el radio del círculo de movimiento.
- Contestar
-
Cruzar multiplicar, luego dividir por el coeficiente de r.
\[\begin{aligned} a &=\frac{v^{2}}{r} \\ a r &=v^{2} \\ r &=\frac{v^{2}}{a} \end{aligned}\]
Para encontrar el radio, sustituya la aceleración\(a=12 \mathrm{m} / \mathrm{s}^{2}\) y la velocidad v = 8 m/s.
\[r=\frac{v^{2}}{a}=\frac{(8)^{2}}{12}=\frac{64}{12}=\frac{16}{3}\]
De ahí que el radio sea\(r=16 / 3 \mathrm{m},\) o 5\(\frac{1}{3}\) metros.
Ejercicio\(\PageIndex{94}\)
Una partícula se mueve a lo largo de una línea con aceleración constante. Se sabe que la velocidad de la partícula, en función de la cantidad de tiempo que ha pasado, viene dada por la ecuación
\[v=v_{0}+a t\]donde v es la velocidad en el tiempo t, v0 es la velocidad inicial de la partícula (en el tiempo t = 0), y a es la aceleración de la partícula.
i. Resolver fórmula (2) para t.
ii. Sabes que la velocidad actual de la partícula es de 120 m/s También sabes que la velocidad inicial fue de 40 m/s y la aceleración ha sido constante\(a=2 \mathrm{m} / \mathrm{s}^{2}\). ¿Cuánto tiempo tardó la partícula en alcanzar su velocidad actual?
Ejercicio\(\PageIndex{95}\)
Al igual que la Ley Universal de Gravitación de Newton, la fuerza de atracción (repulsión) entre dos partículas cargadas a diferencia (como) es proporcional al producto de las cargas e inversamente proporcional a la distancia entre ellas. \[F=k_{C} \frac{q_{1} q_{2}}{r^{2}}\]En esta fórmula,\(k_{C} \approx 8.988 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\) y se llama la constante electrostática. Las variables q1 y q2 representan las cargas (en Coulombs) sobre las partículas (que podrían ser números positivos o negativos) y r representa la distancia (en metros) entre las cargas. Finalmente, F representa la fuerza de la carga, medida en Newtons.
i. Resolver fórmula (3) para r.
ii. Dada una fuerza\(F=2.0 \times 10^{12} \mathrm{N}\), dos cargas iguales\(q_{1}=q_{2}=1 \mathrm{C}\), encuentra la distancia aproximada entre las dos partículas cargadas.
- Contestar
-
Cruzar multiplicar, luego dividir por el coeficiente de r.
\[\begin{aligned} F &=k_{C} \frac{q_{1} q_{2}}{r^{2}} \\ F r^{2} &=k_{C} q_{1} q_{2} \\ r^{2} &=\frac{k_{C} q_{1} q_{2}}{F} \end{aligned}\]
Por último, para encontrar r, tomar la raíz cuadrada.
\[r=\sqrt{\frac{k_{C} q_{1} q_{2}}{F}}\]
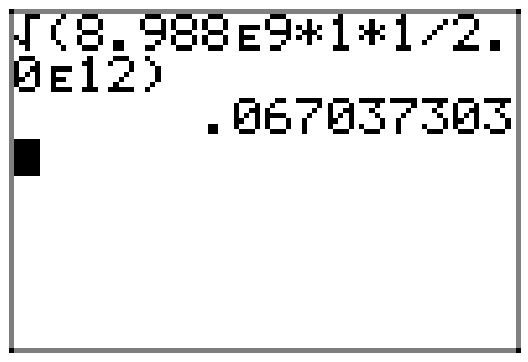
Para encontrar la distancia entre las partículas cargadas, sustituya\(k_{C}=8.988 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2}\),
\(q_{1}=q_{2}=1 \mathrm{C},\) y\(F=2.0 \times 10^{12} \mathrm{N}\).\[r=\sqrt{\frac{\left(8.988 \times 10^{9}\right)(1)(1)}{2.0 \times 10^{12}}}\]
Una calculadora produce una aproximación,\(r \approx 0.067\) metros.
Realizar cada una de las siguientes tareas en Ejercicios\(\PageIndex{96}\) -\(\PageIndex{99}\).
i. Escriba en palabras el significado de los símbolos que están escritos en notación set-builder.
ii. Escribe algunos de los elementos de este conjunto.
iii. Dibuja una línea real y traza algunos de los puntos que hay en este conjunto.
Ejercicio\(\PageIndex{96}\)
\(A=\{x \in \mathbb{N} : x>10\}\)
- Contestar
-
i. A es el conjunto de todos\(x\) en los números naturales tal que\(x\) es mayor que\(10.\)
ii. \(A=\{11,12,13,14, \ldots\}\)
iii.

Ejercicio\(\PageIndex{97}\)
\(B=\{x \in \mathbb{N} : x \geq 10\}\)
Ejercicio\(\PageIndex{98}\)
\(C=\{x \in \mathbb{Z} : x \leq 2\}\)
- Contestar
-
i. C es el conjunto de todos\(x\) en los enteros tal que\(x\) es menor o igual a\(2.\)
ii. \(C=\{\ldots,-4,-3,-2,-1,0,1,2\}\)
iii.

Ejercicio\(\PageIndex{99}\)
\(D=\{x \in \mathbb{Z} : x>-3\}\)
En Ejercicios\(\PageIndex{100}\) -\(\PageIndex{103}\), usa los conjuntos A, B, C y D que se definieron en Ejercicios\(\PageIndex{96}\) -\(\PageIndex{99}\). Describa los siguientes conjuntos usando la notación de conjuntos y dibuje el Diagrama de Venn correspondiente.
Ejercicio\(\PageIndex{100}\)
\(A \cap B\)
- Contestar
-
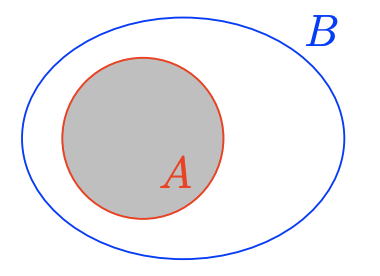
\(A \cap B=\{x \in \mathbb{N} : x>10\}=\{11,12,13, \ldots\}\)
Ejercicio\(\PageIndex{101}\)
\(A \cup B\)
Ejercicio\(\PageIndex{102}\)
\(A \cup C\)
- Contestar
-
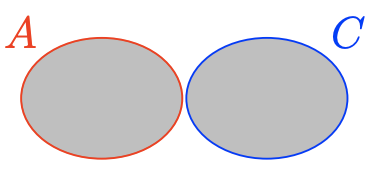
\(A \cup C=\{x \in \mathbb{Z} : x \leq 2 \text { or } x>10\}=\{\ldots,-3,-2-1,0,1,2,11,12,13 \dots\}\)
Ejercicio\(\PageIndex{103}\)
\(C \cap D\)
En Ejercicios\(\PageIndex{104}\) -\(\PageIndex{111}\), use tanto la notación de intervalo como de conjunto para describir el intervalo que se muestra en la gráfica.
Ejercicio\(\PageIndex{104}\)

- Contestar
-
El círculo relleno en el punto final 3 indica que este punto está incluido en el conjunto. Así, el conjunto en notación de intervalo es\([3, \infty)\), y en notación de conjunto\(\{x : x \geq 3\}\).
Ejercicio\(\PageIndex{105}\)

Ejercicio\(\PageIndex{106}\)

- Contestar
-
El círculo vacío en el punto final −7 indica que este punto no está incluido en el conjunto. Así, el conjunto en notación de intervalo es\((-\infty,-7)\), y en notación de conjunto es\(\{x : x<-7\}\).
Ejercicio\(\PageIndex{107}\)

Ejercicio\(\PageIndex{108}\)

- Contestar
-
El círculo vacío en el punto final 0 indica que este punto no está incluido en el conjunto. Así, el conjunto en notación de intervalo es\((0, \infty)\), y en notación de conjunto es\(\{x : x>0\}\).
Ejercicio\(\PageIndex{109}\)

Ejercicio\(\PageIndex{110}\)

- Contestar
-
El círculo vacío en el punto final −8 indica que este punto no está incluido en el conjunto. Así, el conjunto en notación de intervalo es\((-8, \infty)\), y en notación de conjunto es\(\{x : x>-8\}\).
Ejercicio\(\PageIndex{111}\)

En Ejercicios\(\PageIndex{112}\) -\(\PageIndex{119}\), bosquejar la gráfica del intervalo dado.
Ejercicio\(\PageIndex{112}\)
\([2,5)\)
- Contestar
-

Ejercicio\(\PageIndex{113}\)
\((-3,1]\)
Ejercicio\(\PageIndex{114}\)
\([1, \infty)\)
- Contestar
-

Ejercicio\(\PageIndex{115}\)
\((-\infty, 2)\)
Ejercicio\(\PageIndex{116}\)
\(\{x :-4<x<1\}\)
- Contestar
-

Ejercicio\(\PageIndex{117}\)
\(\{x : 1 \leq x \leq 5\}\)
Ejercicio\(\PageIndex{118}\)
\(\{x : x<-2\}\)
- Contestar
-

Ejercicio\(\PageIndex{119}\)
\(\{x : x \geq-1\}\)
En Ejercicios\(\PageIndex{120}\) -\(\PageIndex{127}\), use tanto la notación de intervalo como de conjunto para describir la intersección de los dos intervalos que se muestran en la gráfica. También, esboce la gráfica de la intersección en la recta numérica real.
Ejercicio\(\PageIndex{120}\)
- Contestar
-
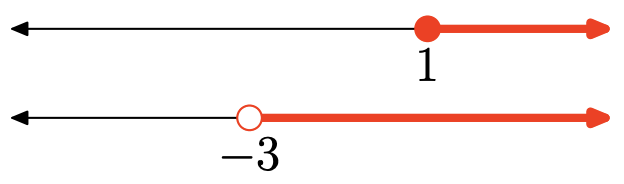
La intersección es el conjunto de puntos que se encuentran en ambos intervalos (sombreados en ambas gráficas). Gráfico de la intersección:

\([1, \infty)=\{x : x \geq 1\}\)
Ejercicio\(\PageIndex{121}\)
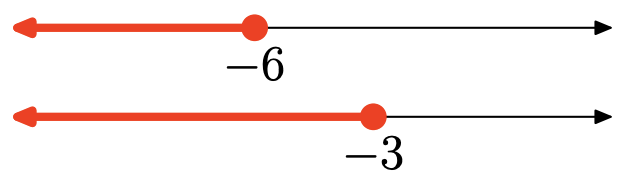
Ejercicio\(\PageIndex{122}\)
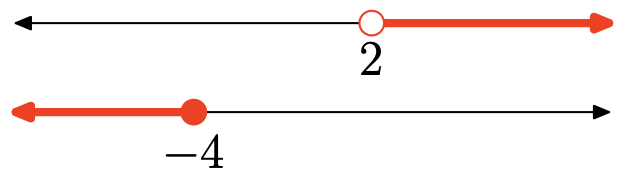
- Contestar
-
No hay puntos que estén en ambos intervalos (sombreados en ambos), por lo que no hay intersección. Gráfico de la intersección:

sin intersección
Ejercicio\(\PageIndex{123}\)
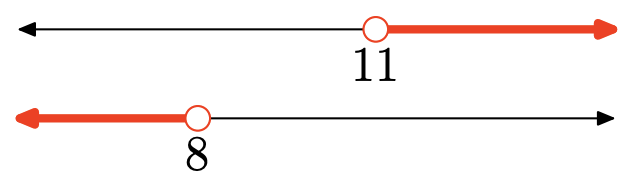
Ejercicio\(\PageIndex{124}\)
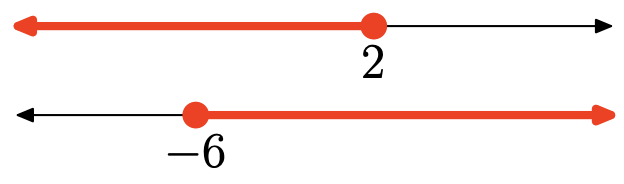
- Contestar
-
La intersección es el conjunto de puntos que se encuentran en ambos intervalos (sombreados en ambos). Gráfico de la intersección:

\([-6,2]=\{x :-6 \leq x \leq 2\}\)
Ejercicio\(\PageIndex{125}\)

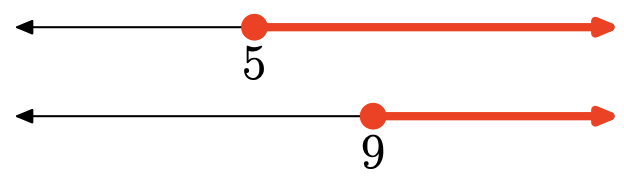
Ejercicio\(\PageIndex{126}\)
- Contestar
-
La intersección es el conjunto de puntos que se encuentran en ambos intervalos (sombreados en ambos). Gráfico de la intersección:

\([9, \infty)=\{x : x \geq 9\}\)
Ejercicio\(\PageIndex{127}\)
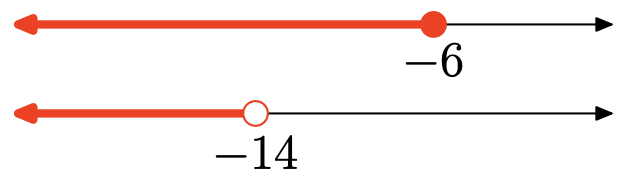
En Ejercicios\(\PageIndex{128}\) -\(\PageIndex{135}\), use tanto la notación de intervalo como de conjunto para describir la unión de los dos intervalos que se muestran en la gráfica. También, esboce la gráfica de la unión en la recta numérica real.
Ejercicio\(\PageIndex{128}\)
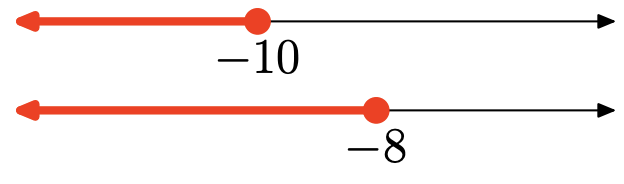
- Contestar
-
La unión es el conjunto de todos los puntos que se encuentran en un intervalo u otro (sombreados en cualquiera de las gráficas). Gráfica de la unión:

\((-\infty,-8]=\{x : x \leq-8\}\)
Ejercicio\(\PageIndex{129}\)

Ejercicio\(\PageIndex{130}\)
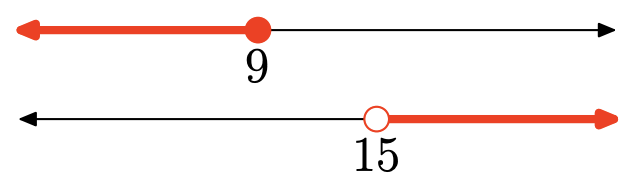
- Contestar
-
La unión es el conjunto de todos los puntos que se encuentran en un intervalo u otro (sombreados en cualquiera de las gráficas). Gráfica de la unión:

\((-\infty, 9] \cup(15, \infty)\)
\(=\{x : x \leq 9 \text { or } x>15\}\)
Ejercicio\(\PageIndex{131}\)
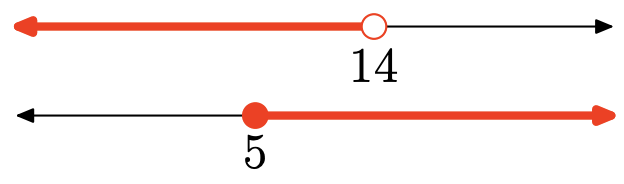
Ejercicio\(\PageIndex{132}\)
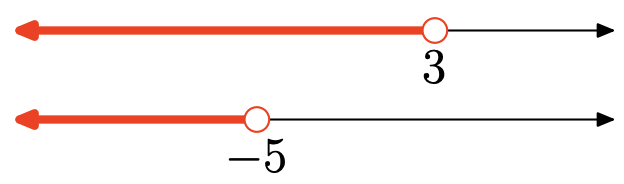
- Contestar
-
La unión es el conjunto de todos los puntos que están en un intervalo u otro (sombreados en cualquiera de ellos). Gráfica de la unión:

\((-\infty, 3)=\{x : x<3\}\)
Ejercicio\(\PageIndex{133}\)
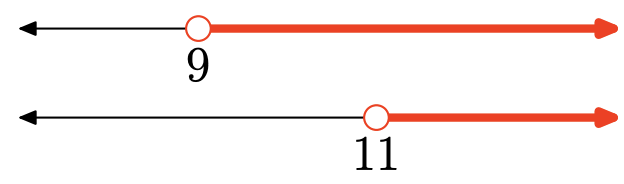
Ejercicio\(\PageIndex{134}\)
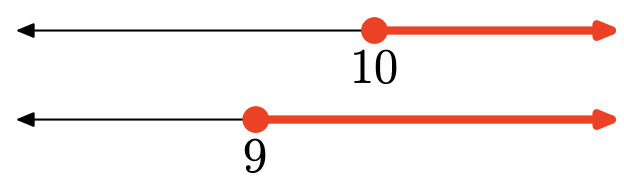
- Contestar
-
La unión es el conjunto de todos los puntos que están en un intervalo u otro (sombreados en cualquiera de ellos). Gráfica de la unión:

\([9, \infty)=\{x : x \geq 9\}\)
Ejercicio\(\PageIndex{135}\)
En Ejercicios\(\PageIndex{136}\) -56, utilice la notación de intervalos para describir el conjunto dado. También, esboce la gráfica del conjunto en la recta numérica real.
Ejercicio\(\PageIndex{136}\)
\(\{x : x \geq-6 \text { and } x>-5\}\)
- Contestar
-
Este conjunto es el mismo que\(\{x : x>-5\}\), que está\((-5, \infty)\) en notación de intervalos. Gráfica del conjunto:

Ejercicio\(\PageIndex{137}\)
\(\{x : x \leq 6 \text { and } x \geq 4\}\)
Ejercicio\(\PageIndex{138}\)
\(\{x : x \geq-1 \text { or } x<3\}\)
- Contestar
-
Cada número real está en uno u otro de los dos intervalos. Por lo tanto, el conjunto es el conjunto de todos los números reales\((-\infty, \infty)\). Gráfica del conjunto:

Ejercicio\(\PageIndex{139}\)
\(\{x : x>-7 \text { and } x>-4\}\)
Ejercicio\(\PageIndex{140}\)
\(\{x : x \geq -1 \text { or } x>6\}\)
- Contestar
-
Este conjunto es el mismo que\(\{x : x \geq-1\}\), que está\([-1, \infty)\) en notación de intervalos. Gráfica del conjunto:

Ejercicio\(\PageIndex{141}\)
\(\{x : x \geq 7 \text { or } x<-2\}\)
Ejercicio\(\PageIndex{142}\)
\(\{x : x \geq 6 \text { or } x>-3\}\)
- Contestar
-
Este conjunto es el mismo que\(\{x : x>-3\}\), que está\((-3, \infty)\) en notación de intervalos. Gráfica del conjunto:

Ejercicio\(\PageIndex{143}\)
\(\{x : x \leq 1 \text { or } x>0\}\)
Ejercicio\(\PageIndex{144}\)
\(\{x : x<2 \text { and } x<-7\}\)
- Contestar
-
Este conjunto es el mismo que\(\{x : x<-7\}\), que está\((-\infty,-7)\) en notación de intervalos. Gráfica del conjunto:

Ejercicio\(\PageIndex{145}\)
\(\{x : x \leq-3 \text { and } x<-5\}\)
Ejercicio\(\PageIndex{146}\)
\(\{x : x \leq-3 \text { or } x \geq 4\}\)
- Contestar
-
Este conjunto es la unión de dos intervalos,\((-\infty,-3] \cup[4, \infty)\). Gráfica del conjunto:

Ejercicio\(\PageIndex{147}\)
\(\{x : x<11 \text { or } x \leq 8\}\)
Ejercicio\(\PageIndex{148}\)
\(\{x : x \geq 5 \text { and } x \leq 1\}\)
- Contestar
-
No hay números que satisfagan ambas desigualdades. Por lo tanto, no hay intersección. Gráfica del conjunto:

Ejercicio\(\PageIndex{149}\)
\(\{x : x<5 \text { or } x<10\}\)
Ejercicio\(\PageIndex{150}\)
\(\{x : x \leq 5 \text { and } x \geq-1\}\)
- Contestar
-
Este conjunto es el mismo que\(\{x :-1 \leq x \leq 5\}\), que es [−1, 5] en notación de intervalo. Gráfica del conjunto

Ejercicio\(\PageIndex{151}\)
\(\{x : x>-3 \text { and } x<-6\}\)
En Ejercicios\(\PageIndex{152}\) -\(\PageIndex{163}\), resolver la desigualdad. Exprese su respuesta tanto en intervalos como en anotaciones establecidas, y sombree la solución en una línea numérica.
Ejercicio\(\PageIndex{152}\)
\(-8 x-3 \leq-16 x-1\)
- Contestar
-
\[\begin{aligned} & -8 x-3 \leq-16 x-1 \\ \Longrightarrow \quad & − 8x + 16x \leq −1 + 3 \\ \Longrightarrow \quad& 8x \leq 2 \\ \Longrightarrow \quad & x \leq \frac{1}{4}\end{aligned}\]
Así, el intervalo de solución es\((−\infty, \frac{1}{4}]\) =\(\{x|x \leq \frac{1}{4}\}\).

Ejercicio\(\PageIndex{153}\)
\(6 x-6>3 x+3\)
Ejercicio\(\PageIndex{154}\)
\(-12 x+5 \leq-3 x-4\)
- Contestar
-
\[\begin{aligned} & -12 x+5 \leq-3 x-4 \\ \Longrightarrow \quad & -12x + 3x \leq −4 − 5 \\ \Longrightarrow \quad& -9x \leq -9 \\ \Longrightarrow \quad & x \geq 1\end{aligned}\]
Así, el intervalo de solución es\([1,\infty) = \{x|x \geq 1\}\).

Ejercicio\(\PageIndex{155}\)
\(7 x+3 \leq-2 x-8\)
Ejercicio\(\PageIndex{156}\)
\(-11 x-9<-3 x+1\)
- Contestar
-
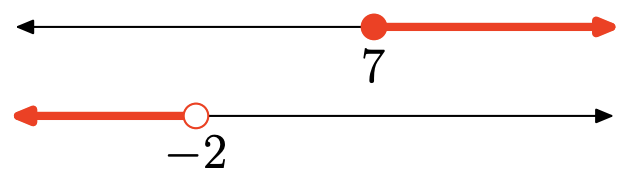
\[\begin{aligned} & − 11x − 9 < −3x + 1 \\ \Longrightarrow \quad & − 11x + 3x < 1 + 9 \\ \Longrightarrow \quad& − 8x < 10 \\ \Longrightarrow \quad & x > -\frac{5}{4}\end{aligned}\]
Así, el intervalo de solución es\((−\frac{5}{4} ,\infty) = \{x|x >−\frac{5}{4} \}\).
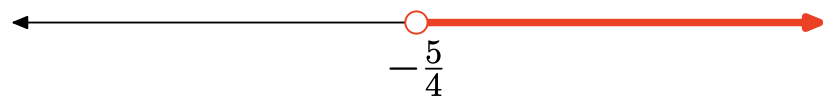
Ejercicio\(\PageIndex{157}\)
\(4 x-8 \geq-4 x-5\)
Ejercicio\(\PageIndex{158}\)
\(4 x-5>5 x-7\)
- Contestar
-
\[\begin{aligned} & 4x − 5 > 5x − 7\\ \Longrightarrow \quad & 4x − 5x > −7 + 5 \\ \Longrightarrow \quad& − x > −2 \\ \Longrightarrow \quad &x < 2\end{aligned}\]
Así, el intervalo de solución es\((−\infty, 2) = \{x|x < 2\}\).
Ejercicio\(\PageIndex{159}\)
\(-14 x+4>-6 x+8\)
Ejercicio\(\PageIndex{160}\)
\(2 x-1>7 x+2\)
- Contestar
-
\[\begin{aligned} & 2x − 1 > 7x + 2\\ \Longrightarrow \quad & 2x − 7x > 2 + 1 \\ \Longrightarrow \quad& − 5x > 3 \\ \Longrightarrow \quad &x < −\frac{3}{5}\end{aligned}\]
Así, el intervalo de solución es\((−\infty, −\frac{3}{5}) = \{x|x < −\frac{3}{5}\}\).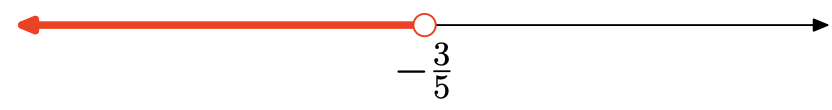
Ejercicio\(\PageIndex{161}\)
\(-3 x-2>-4 x-9\)
Ejercicio\(\PageIndex{162}\)
\(-3 x+3<-11 x-3\)
- Contestar
-
\[\begin{aligned} & − 3x + 3 < −11x − 3\\ \Longrightarrow \quad & − 3x + 11x < −3 − 3 \\ \Longrightarrow \quad& 8x < −6 \\ \Longrightarrow \quad &x < -\frac{3}{4}\end{aligned}\]
Así, el intervalo de solución es\((−\infty, −\frac{3}{4}) = \{x|x < −\frac{3}{4}\}\).
Ejercicio\(\PageIndex{163}\)
\(6 x+3<8 x+8\)
En los Ejercicios 13-50, resolver la desigualdad compuesta. Exprese su respuesta tanto en intervalos como en anotaciones establecidas, y sombree la solución en una línea numérica.
Ejercicio\(\PageIndex{164}\)
\(2 x-1<4\)o\(7 x+1 \geq-4\)
- Contestar
-
\[\begin{aligned} & 2x − 1 < 4 \text{ or } 7x + 1 \geq −4\\ \Longrightarrow \quad & 2x < 5\quad \text{or}\quad 7x \geq −5 \\ \Longrightarrow \quad&x<\frac{5}{2}\quad\text{or}\quad x\geq-\frac{5}{7}\end{aligned}\]

Para la unión, sombree cualquier cosa sombreada en cualquiera de las gráficas. La solución es el conjunto de todos los números reales\((−\infty,\infty)\).

Ejercicio\(\PageIndex{165}\)
\(-8 x+9<-3\)y\(-7 x+1>3\)
Ejercicio\(\PageIndex{166}\)
\(-6 x-4<-4\)y\(-3 x+7 \geq-5\)
- Contestar
-
\[\begin{aligned} & − 6x − 4 < −4 \text{ and } − 3x + 7 \geq −5\\ \Longrightarrow \quad & -6x < 0\quad \text{and}\quad -3x \geq −12 \\ \Longrightarrow \quad&x>0\quad\text{and}\quad x\leq4 \\ \Longrightarrow \quad & 0< x \leq 4 \end{aligned}\]
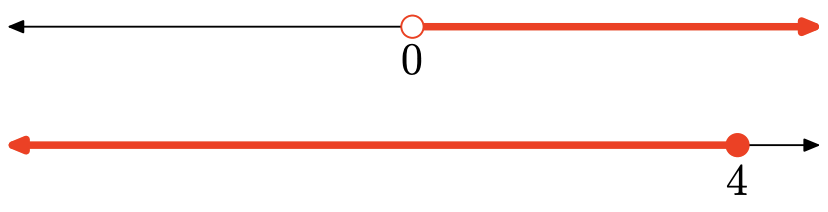
La intersección es todos los puntos sombreados en ambas gráficas, por lo que la solución es\((0, 4] = \{x|0 < x \leq 4\}\).

Ejercicio\(\PageIndex{167}\)
\(-3 x+3 \leq 8\)y\(-3 x-6>-6\)
Ejercicio\(\PageIndex{168}\)
\(8 x+5 \leq-1\)y\(4 x-2>-1\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{169}\)
\(-x-1<7\)y\(-6 x-9 \geq 8\)
Ejercicio\(\PageIndex{170}\)
\(-3 x+8 \leq-5\)o\(-2 x-4 \geq-3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{171}\)
\(-6 x-7<-3\)y\(-8 x \geq 3\)
Ejercicio\(\PageIndex{172}\)
\(9 x-9 \leq 9\)y\(5 x>-1\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-7 x+3<-3\)o\(-8 x \geq 2\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(3 x-5<4\)y\(-x+9>3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-8 x-6<5\)o\(4 x-1 \geq 3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(9 x+3 \leq-5\)o\(-2 x-4 \geq 9\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-7 x+6<-4\)o\(-7 x-5>7\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(4 x-2 \leq 2\)o\(3 x-9 \geq 3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-5 x+5<-4\)o\(-5 x-5 \geq-5\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(5 x+1<-6\)y\(3 x+9>-4\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(7 x+2<-5\)o\(6 x-9 \geq-7\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-7 x-7<-2\)y\(3 x \geq 3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(4 x+1<0\)o\(8 x+6>9\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(7 x+8<-3\)y\(8 x+3 \geq-9\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(3 x<2\)y\(-7 x-8 \geq 3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-5 x+2 \leq-2\)y\(-6 x+2 \geq 3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(4 x-1 \leq 8\)o\(3 x-9>0\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(2 x-5 \leq 1\)y\(4 x+7>7\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(3 x+1<0\)o\(5 x+5>-8\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-8 x+7 \leq 9\)o\(-5 x+6>-2\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(x-6 \leq-5\)y\(6 x-2>-3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-4 x-8<4\)o\(-4 x+2>3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(9 x-5<2\)o\(-8 x-5 \geq-6\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-9 x-5 \leq-3\)o\(x+1>3\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-5 x-3 \leq 6\)y\(2 x-1 \geq 6\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-1 \leq-7 x-3 \leq 2\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(0<5 x-5<9\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(5<9 x-3 \leq 6\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-6<7 x+3 \leq 2\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-2<-7 x+6<6\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-9<-2 x+5 \leq 1\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
En los Ejercicios 51-62, resuelva la desigualdad dada para x. Grafique el conjunto de soluciones en una línea numérica, luego use la notación interval y set-builder para describir el conjunto de soluciones.
Ejercicio\(\PageIndex{1}\)
\(-\frac{1}{3}<\frac{x}{2}+\frac{1}{4}<\frac{1}{3}\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-\frac{1}{5}<\frac{x}{2}-\frac{1}{4}<\frac{1}{5}\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-\frac{1}{2}<\frac{1}{3}-\frac{x}{2}<\frac{1}{2}\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-\frac{2}{3} \leq \frac{1}{2}-\frac{x}{5} \leq \frac{2}{3}\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-1<x-\frac{x+1}{5}<2\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-2<x-\frac{2 x-1}{3}<4\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-2<\frac{x+1}{2}-\frac{x+1}{3} \leq 2\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-3<\frac{x-1}{3}-\frac{2 x-1}{5} \leq 2\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(x<4-x<5\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-x<2 x+3 \leq 7\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(-x<x+5 \leq 11\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
\(−2x < 3 − x \leq 8\)
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Aeron ha organizado una demostración de “Cómo hacer un cometa” a cargo del profesor O'Commel. El sabio profesor le ha pedido a Aeron que se asegure de que el auditorio se mantenga entre 15 y 20 grados centígrados (C). Aeron sabe que el termostato está en Fahrenheit (F) y también sabe que la fórmula de conversión entre las dos escalas de temperatura es C = (5/9) (F − 32).
a) Establecer la desigualdad compuesta para el rango de temperatura solicitado en Celsius, obtenemos\(15 \leq C \leq 20\). Usando la fórmula de conversión anterior, establecer la desigualdad compuesta correspondiente en Fahrenheit.
b) Resolver la desigualdad compuesta en la parte (a) para F. Escribe tu respuesta en notación fija.
c) ¿Cuáles son las temperaturas posibles (solo enteros) en las que Aeron puede ajustar el termostato en Fahrenheit?
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Ejercicio\(\PageIndex{1}\)
Agrega texto de ejercicios aquí.
- Contestar
-
Agrega textos aquí. No borre primero este texto.

