1.3: Lógica
- Page ID
- 110719
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dos de las palabras más sutiles en el idioma inglés son las palabras “y” y “o”. Una tiene sólo tres letras, las otras dos, pero es absolutamente sorprendente cuánta confusión pueden causar estas dos diminutas palabras. Nuestra intención en esta sección es aclarar el misterio que rodea estas palabras y prepararte para las matemáticas que dependen de una comprensión profunda de las palabras “y” y “o”.
Notación de conjunto
Comenzamos con la definición de un conjunto.
Definición 1
Un conjunto es una colección de objetos.
Los objetos en el conjunto podrían ser cualquier cosa: números, letras, nombres, ciudades, lo que sea. En esta sección nos centraremos en conjuntos de números, pero es importante entender que los objetos de un conjunto pueden ser lo que tú elijas que sean.
Si el número de objetos en un conjunto es finito y lo suficientemente pequeño, podemos describir el conjunto simplemente enumerando los elementos (objetos) en el conjunto. Esto generalmente se hace encerrando la lista de objetos en el conjunto con llaves. Por ejemplo, vamos
\[A=\{1,3,5,7,9,11\}\]
Ahora bien, cuando nos referimos al set\(A\) en la narrativa, todos deberían saber que estamos hablando del conjunto de números 1, 3, 5, 7, 9 y 11.
También es posible describir el conjunto\(A\) con palabras. Aunque hay muchas formas de hacerlo, una posible descripción podría ser “\(A\)Sea el conjunto de números naturales impares entre 1 y 11, inclusive”. Esta técnica descriptiva es particularmente eficiente cuando el conjunto que está describiendo es infinito o demasiado grande para enumerarlo en una lista.
Por ejemplo, podríamos decir “dejemos\(A\) ser el conjunto de todos los números reales que sean mayores que\(4.\)” Esto es mucho mejor que tratar de enumerar cada uno de los números del conjunto\(A\), lo que sería inútil en este caso. Otra posibilidad es combinar la notación de llaves rizadas con una descripción textual y escribir algo así como
\[A=\{ \text{real numbers that are greater than }4\}\]
Si se nos llama a leer esta notación en voz alta, diríamos “\(A\)es el conjunto de todos los números reales que son mayores que\(4,\)” o algo similar.
Hay una serie de métodos más sofisticados que podemos usar para describir un conjunto. Una descripción que emplearemos a menudo se llama notación set-builder y tiene la siguiente apariencia.
\[A=\{x : \text{some statement describing }x\}\]
Es estándar leer la notación en\(\{x : \quad\}\) voz alta de la siguiente manera: “El conjunto de todos\(x\) tales que”. Es decir, el colon se pronuncia “tal que”. Entonces leerías la descripción que sigue a los dos puntos. Por ejemplo, el conjunto
\[A=\{x : x<3\}\]
se lee en voz alta “\(A\)es el conjunto de todos\(x\) tales que\(x\) es menor que\(3.\)” Algunas personas prefieren usar una “barra” en lugar de dos puntos y escriben
\[A=\{x \, | \,\text { some statement describing } x\}\]
Esto también se pronuncia “\(A\)es el conjunto de todo\(x\) tal que”, y luego se leería la descripción del texto que sigue a la “barra”. Así, la notación
\[A=\{x \, | \, x<3\}\]
es idéntica a la notación\(A=\{x : x<3\}\) utilizada anteriormente y se lee exactamente de la misma manera, “A es el conjunto de todos los\(x\) tales que\(x\) es menor que 3”. Preferimos la notación de dos puntos, pero siéntete libre de usar la “barra” si te gusta más. Significa lo mismo.
El pensamiento de un momento revelará el hecho de que la notación no\(A=\{x : x<3\}\) es lo suficientemente descriptiva. Probablemente sea seguro decirlo, ya que la descripción de\(x\) es “\(x < 3,\)” que esta notación se refiere a números que son menores a 3, pero ¿qué tipo de números? ¿Números naturales? ¿Enteros? ¿Números racionales? ¿Números irracionales? ¿Números reales? La notación realmente\(A=\{x : x<3\}\) no cuenta toda la historia.
Arreglaremos esta deficiencia en un momento, pero primero recordemos que en nuestro capítulo preliminar, usamos símbolos específicos para representar ciertos conjuntos de números. En efecto, utilizamos lo siguiente:
\[\begin{aligned} \mathbb{N} &=\{\text { natural numbers }\} \\ \mathbb{Z} &=\{\text { integers }\} \\ \mathbb{Q} &=\{\text { rational numbers }\} \\ \mathbb{R} &=\{\text { real numbers }\} \end{aligned}\]
Podemos usar estos símbolos para ayudar a denotar el tipo de número descrito con nuestra notación setbuilder. Por ejemplo, si escribimos
\[A=\{x \in \mathbb{N} : x<3\}\]
entonces decimos “A es el conjunto de todos los x en los números naturales de tal manera que x es menor que 3”, o más simplemente, “el conjunto de todos los números naturales que son menores que 3”. El símbolo\(∈\) es la letra griega “épsilon”, y cuando se usa en la notación set-builder, se pronuncia “es un elemento de” o “está en”. Por supuesto, los únicos números naturales\(\mathbb{N}=\{1,2,3, \ldots\}\) que son menores a 3 son los números naturales 1 y 2. Así,\(A = {1, 2}\), el “conjunto cuyos integrantes son 1 y 2”.
Por otro lado, si escribimos
\[A=\{x \in \mathbb{Z} : x<3\}\]
entonces decimos que “\(A\)es el conjunto de\(x\) en el conjunto de enteros tal que\(x\) es menor que 3”, o más informalmente, “\(A\)es el conjunto de todos los enteros menores que 3”. Por supuesto, los enteros\(\mathbb{Z}=\{0, \pm 1, \pm 2, \pm 3, \ldots\}^{2}\) menores que 3 son infinitos en número. No podemos enumerarlos a todos a menos que apelemos a la imaginación con algo así como
\[A=\{\ldots,-3,-2,-1,0,1,2\}\]
Los puntos suspensivos.. significa “etc.” Hemos enumerado suficientes números para establecer un patrón, así que se nos permite decir “y así sucesivamente”. El lector intuye que los números anteriores en la lista son −4, −5, etc.
Veamos otro ejemplo. Supongamos que escribimos\[A=\{x \in \mathbb{R} : x<3\}\]
Entonces decimos “\(A\)es el conjunto de todos\(x\) en el conjunto de números reales tal que\(x\) es menor que 3”, o más informalmente, “\(A\)es el conjunto de todos los números reales menores que 3”. Por supuesto, este es otro conjunto infinito y no es difícil imaginar que la notación\(\{x \in \mathbb{R} : x<3\}\) utilizada anteriormente ya sea óptima para describir este conjunto de números reales.
En este texto, trataremos mayoritariamente conjuntos de números reales. Así, a partir de este punto, si escribimos
\[A=\{x : x<3\}\]
vamos a suponer que queremos decir que “\(A\)es el conjunto de todos los números reales menores a 3”. Es decir, si escribimos\(A=\{x : x<3\}\), entendemos que esto significa\(A=\{x \in \mathbb{R} : x<3\}\). En el caso de que queramos usar un conjunto específico de números, indicaremos que como hicimos anteriormente, por ejemplo, en\(A=\{x \in \mathbb{N} : x<3\}\).
La notación real de línea e intervalo
Supongamos que dibujamos una línea (cariñosamente conocida como la “línea real”), luego trazamos un punto en cualquier parte de esa línea, luego mapeamos el número cero a ese punto (llamado el “origen”), como se muestra en la Figura\(\PageIndex{1}\). En segundo lugar, decidir una distancia unitaria y mapear el número 1 a ese punto, nuevamente mostrado en la Figura\(\PageIndex{1}\).
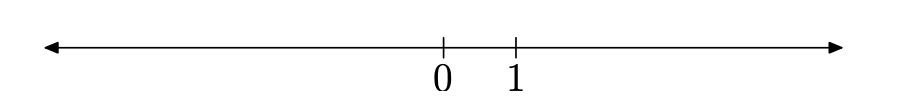
Ahora que hemos establecido una distancia unitaria, cada número real corresponde a un punto en la línea real. Viceversa, cada punto de la línea real corresponde a un número real. Esto define una correspondencia uno a uno entre los números reales en\(\mathbb{R}\) y los puntos en la línea real. De esta manera, el punto en la línea y el número real pueden ser pensados como sinónimos. La figura\(\PageIndex{2}\) muestra varios números reales trazados en la línea real.
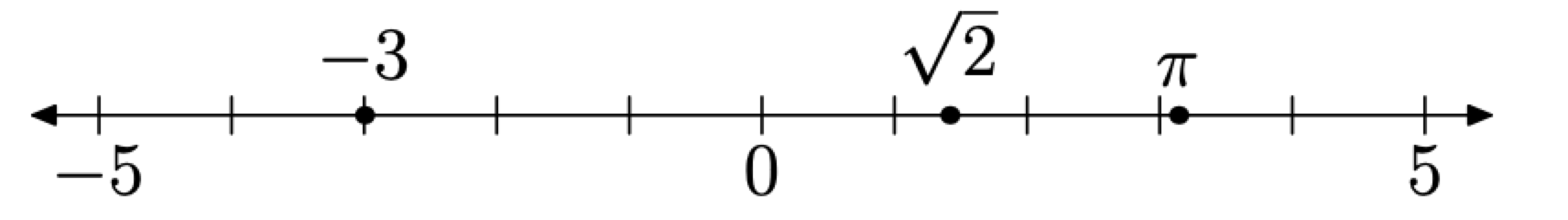
Figura Números\(\PageIndex{2}\) de muestra en la línea real.
Ahora, supongamos que se nos pide que sombreemos todos los números reales del set\(\{x : x>3\}\). Debido a que esto requiere que sombreemos cada número real que sea mayor que 3 (a la derecha de 3), usamos el sombreado que se muestra en la Figura\(\PageIndex{3}\) para representar el conjunto\(\{x : x>3\}\).
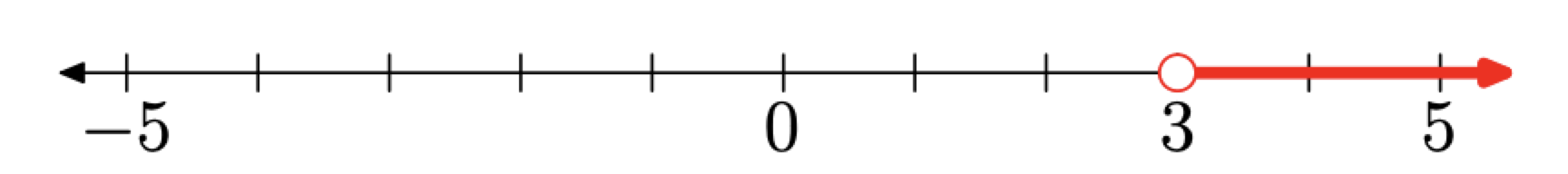
Aunque técnicamente correcta, la imagen de la Figura 3 contiene más información de la que realmente se necesita. El panorama es aceptable, pero abarrotado. La información realmente importante es el hecho de que el sombreado comienza a las 3, luego se mueve hacia la derecha. Además, debido a que 3 no está en el conjunto\({x : x > 3}\), es decir, 3 no es mayor que 3, no sombreamos el punto correspondiente al número real 3. Tenga en cuenta que hemos indicado este hecho con un círculo “vacío” a las 3 en la línea real.
Así, al sombrear el conjunto\({x : x > 3}\) en la línea real, solo necesitamos etiquetar el punto final en 3, usar un círculo “vacío” en 3 y sombrear todos los números reales a la derecha de 3, como se muestra en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\). Sombreando todos los números reales mayores a 3. El punto final es la única información que necesita ser etiquetada. No es necesario mostrar ningún otro tickpoints y/o etiquetas.
Debido a que estamos sombreando todos los números del 3 al infinito positivo en la Figura\(\PageIndex{4}\), usaremos la siguiente notación de intervalo para representar este “intervalo” de números (todo entre 3 e infinito positivo).
\[(3, \infty)=\{x : x>3\}\]
De igual manera, Table\(\PageIndex{1}\) enumera las notaciones de set-builder e interval, así como el sombreado de los conjuntos en la línea real, para varias situaciones, entre ellas la que se acaba de discutir.
Hay varios puntos de énfasis respecto a los intervalos en la Tabla\(\PageIndex{1}\).
1. Cuando queremos enfatizar que no estamos incluyendo un punto en la línea real, usamos un “círculo vacío”. Por el contrario, un “círculo lleno” significa que estamos incluyendo el punto en la línea real. Así, las líneas reales en las dos primeras filas de Table\(\PageIndex{1}\) no incluyen el número 3, pero las líneas reales en las dos últimas filas de Table\(\PageIndex{1}\) sí incluyen el número 3.
2. El uso de un paréntesis en la notación de intervalo significa que no estamos incluyendo ese punto final en el intervalo. Así, el uso de paréntesis\((-\infty, 3)\) en la segunda fila de Table\(\PageIndex{1}\) significa que no estamos incluyendo el número 3 en el intervalo.
| Línea numéricos | Notación Set-Builder | Notación de intervalos |
|---|---|---|
 |
\(\{x : x > 3\}\) | \((3, \infty)\) |
 |
\(\{x : x < 3\}\) | \((-\infty, 3)\) |
 |
\(\{x : x \geq 3\}\) | \([3, \infty)\) |
 |
\(\{x : x \leq 3\}\) | \((-\infty, 3]\) |
3. El uso de un corchete en la notación de intervalo significa que estamos incluyendo el número entre corchetes en el intervalo. Así, el corchete utilizado en\([3, \infty)\), como se ve en la tercera fila de Tabla\(\PageIndex{1}\), significa que estamos incluyendo el número 3 en el intervalo.
4. El uso de\(\infty\)\((3, \infty)\) en la fila uno de Tabla\(\PageIndex{1}\) significa que estamos incluyendo cada número real mayor que 3. El uso de\(-\infty\) in\((-\infty, 3]\) significa que estamos incluyendo cada número real menor o igual a 3. Como\(-\infty\) y no\(\infty\) son números reales, no tiene sentido incluirlos con un paréntesis. En consecuencia, siempre se debe usar un paréntesis con\(-\infty\) o\(\infty\).
Unión e intersección
La intersección de dos conjuntos\(A\) y\(B\) se define de la siguiente manera.
Definición 3
La intersección de los conjuntos\(A\) y\(B\) es el conjunto de todos los objetos que están dentro\(A\) y dentro\(B\). En símbolos, escribimos
\[A \cap B=\{x : x \in A \text { and } x \in B\}\]
Para entender esta definición, es absolutamente crucial que entendamos el significado de la palabra “y”. La palabra “y” es una conjunción, utilizada entre declaraciones\(P\) y\(Q\), como en “Hoy está lloviendo y mi mejor amigo es el Llanero Solitario”. Para determinar la verdad o falsedad de esta afirmación, primero debe examinar la verdad o falsedad de las afirmaciones\(P\) y a cada\(Q\) lado de la palabra “y”.
La única forma en que el hablante está diciendo la verdad es si ambas declaraciones\(P\) y\(Q\) son verdaderas. Es decir, la afirmación “Hoy está lloviendo y mi mejor amigo es el Llanero Solitario” es cierta si y sólo si la afirmación “Hoy está lloviendo” es cierta y la afirmación “mi mejor amigo es el Llanero Solitario” también es cierta. A los logísticos les gusta componer un constructo llamado tabla de verdad, como el que se muestra en Tabla\(\PageIndex{2}\).
Puntos en la Tabla\(\PageIndex{2}\) a considerar:
| \(P\) | \(Q\) | \(P\)y\(Q\) |
|---|---|---|
| \ (P\) ">T | \ (Q\) ">T | \ (P\) y\(Q\) “>T |
| \ (P\) ">T | \ (Q\) ">F | \ (P\) y\(Q\) “>F |
| \ (P\) ">F | \ (Q\) ">T | \ (P\) y\(Q\) “>F |
| \ (P\) ">F | \ (Q\) ">F | \ (P\) y\(Q\) “>F |
- En la primera fila (después de la fila de encabezado) de Table\(\PageIndex{2}\), si las declaraciones\(P\) y\(Q\) son ambas verdaderas (indicadas con una T), entonces la sentencia “\(P\)y\(Q\)” también es verdadera.
- En las filas restantes de Table\(\PageIndex{2}\), una u otra de declaraciones\(P\) o\(Q\) son falsas (indicadas con una F), por lo que la sentencia “\(P\)y\(Q\)” también es falsa.
Por lo tanto, la afirmación “\(P\)y\(Q\)” es verdadera si y sólo si\(P\) es verdadera y\(Q\) es verdadera.
Ejemplo\(\PageIndex{1}\)
Si\(A = \{1, 3, 5, 7, 9\}\) y\(B = \{2, 5, 7, 8, 11\},\) encontrar la intersección de\(A\) y\(B.\)
Solución
Como recordatorio, la intersección de conjuntos\(A\) y\(B\) es
\[A \cap B=\{x : x \in A \text { and } x \in B\}\]
Así, estamos buscando los objetos que están en\(A\) y en\(B.\) Los únicos objetos que están en\(A\) y en\(B\) (recuerde, ambas declaraciones “in\(A\)” y “in\(B\)” deben ser verdaderas) son 5 y 7, así que escribimos:
\[A \cap B=\{5,7\}\]
Tanto matemáticos como logísticos utilizan una ayuda visual llamada Diagrama de Venn para representar conjuntos. John Venn fue un matemático inglés que ideó esta visualización de las relaciones lógicas. Considera la elipse\(A\) en la Figura\(\PageIndex{5}\). Todo dentro del límite de esta elipse constituye el conjunto Por\(A = \{1, 3, 5, 7, 9\}.\) eso ves estos números dentro del límite de esta elipse.
Considera la elipse\(B\) en la Figura\(\PageIndex{5}\). Todo dentro del límite de esta elipse constituye el conjunto Por\(B = \{2, 5, 7, 8, 11\}.\) eso ves estos números dentro del límite de esta elipse.
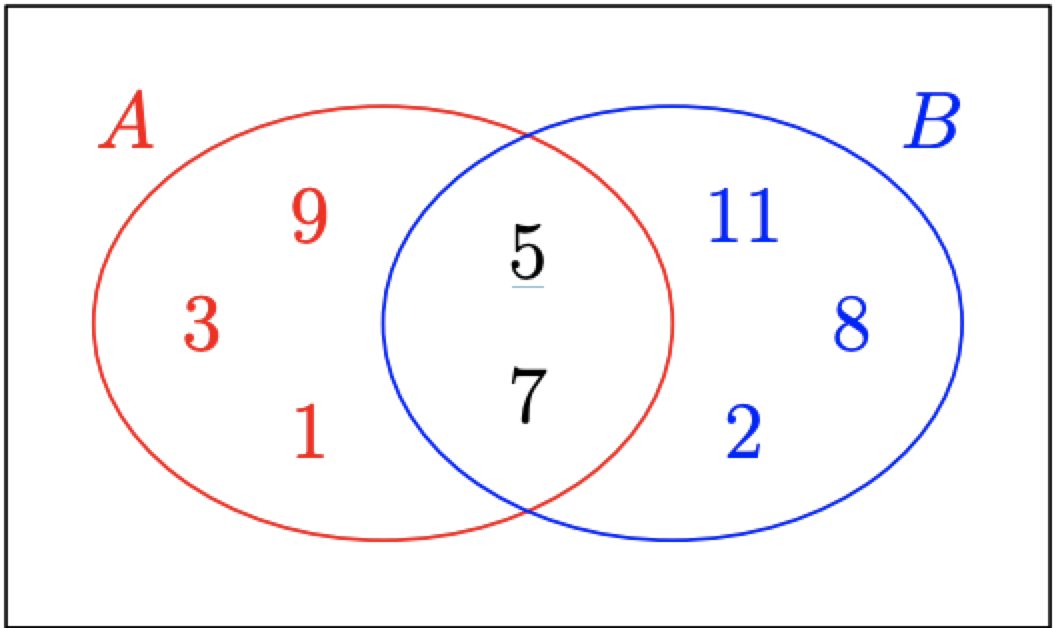
Ahora, tenga en cuenta que sólo dos números,\(5\) y\(7,\) están contenidos dentro de los límites de ambos\(A\) y\(B.\) Estos son los números que están en la intersección de los conjuntos\(A\) y\(B.\)
La región sombreada en la Figura\(\PageIndex{6}\) es el área que pertenece a ambos conjuntos\(A\) y\(B.\) Observe cómo esta región sombreada se denomina acertadamente “la intersección de los conjuntos\(A\) y\(B.\)” Esta es la región que es común a los conjuntos\(A\) y\(B,\) la región donde se encuentra el establece\(A\) y\(B\) se superponen o “se cruzan”.
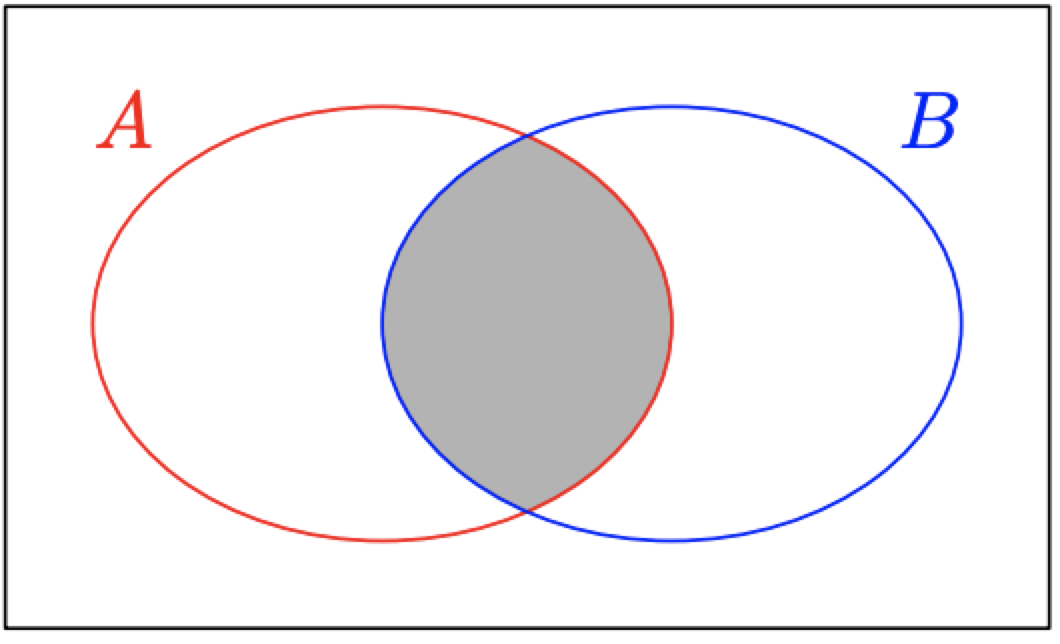
Esto lleva al siguiente consejo importante.
Nota
Cuando se le pide encontrar la intersección de dos conjuntos\(A\) y\(B,\) buscar para ver dónde se cruzan o se superponen los conjuntos. Es decir, mirar para ver los elementos que están en ambos conjuntos\(A\) y\(B.\)
Pasemos a la definición de la unión de dos conjuntos\(A\) y\(B.\)
Definición
La unión de los conjuntos\(A\) y\(B\) es el conjunto de todos los objetos que están en\(A\) o\(B.\) en símbolos, escribimos
\[A \cup B=\{x : x \in A \text { or } x \in B\}\]
Para entender esta definición, es fundamental que entendamos el significado de la palabra “o”. La palabra “o” es una disyunción, utilizada entre declaraciones\(P\) y\(Q,\) como en “Hoy está lloviendo o mi mejor amigo es el Llanero Solitario”. Para determinar la verdad o falsedad de esta afirmación, primero debe examinar la verdad o falsedad de las afirmaciones\(P\) y a cada\(Q\) lado de la palabra “o”.
El orador está diciendo la verdad si cualquiera de las dos\(P\) afirmaciones es verdadera o la declaración\(Q\) es cierta. Es decir, la afirmación “Hoy está lloviendo o mi mejor amigo es el Llanero Solitario” es cierta si y sólo si la afirmación “Hoy está lloviendo” es cierta o la afirmación “mi mejor amigo es el Llanero Solitario” es cierta. A los logísticos les gusta componer un constructo llamado tabla de verdad, como el que se muestra en Tabla\(\PageIndex{3}\).
| \(P\) | \(Q\) | \(P\)o\(Q\) |
|---|---|---|
| \ (P\) ">T | \ (Q\) ">T | \ (P\) o\(Q\) “>T |
| \ (P\) ">T | \ (Q\) ">F | \ (P\) o\(Q\) “>T |
| \ (P\) ">F | \ (Q\) ">T | \ (P\) o\(Q\) “>T |
| \ (P\) ">F | \ (Q\) ">F | \ (P\) o\(Q\) “>F |
Puntos en la Tabla\(\PageIndex{3}\) a considerar:
- En la última fila de Table\(\PageIndex{3}\), ambas declaraciones\(P\) y\(Q\) son falsas (se indica con una F), por lo que la sentencia\(P\) o también\(Q\) es falsa.
- En las tres primeras filas (después de la fila de encabezado) de Table\(\PageIndex{3}\), ya sea sentencia\(P\) es verdadera o declaración\(Q\) es verdadera (indicada con una T), por lo que la sentencia\(P\) o también\(Q\) es verdadera.
Por lo tanto, la afirmación “\(P\)o\(Q\)” es verdadera si y sólo si alguna declaración,\(P\) o\(Q,\) es verdadera.
Ejemplo\(\PageIndex{2}\)
Si\(A = \{1, 3, 5, 7, 9\}\) y\(B = \{2, 5, 7, 8, 11\},\) encontrar la unión de\(A\) y\(B.\)
Solución
Como recordatorio, la unión de\(A\) y\(B\) es\[A \cup B=\{x : x \in A \text { or } x \in B\}\]
Así, un objeto está en la unión de\(A\) y\(B\) si y sólo si está en cualquiera de los conjuntos. Los números que están en cualquiera de los conjuntos son los números\[A \cup B=\{1,2,3,5,7,8,9,11\}\]
Si volvemos a mirar el Diagrama de Venn en la Figura\(\PageIndex{5}\), vemos que esta unión\(A \cup B = \{1, 2, 3, 5, 7, 8, 9, 11\}\) enumera cada número que está en cualquiera de los dos conjuntos de la Figura\(\PageIndex{5}\).
Así, la región sombreada en Figura\(\PageIndex{7}\) es la unión de conjuntos\(A\) y\(B.\) Observe cómo esta región es bien nombrada, ya que eso es lo que realmente estás haciendo, tomando la “unión” de los dos conjuntos\(A\) y es\(B.\) decir, la unión contiene todos los elementos que pertenecen a cualquiera\(A\) o \(B.\)De manera menos formal, la unión es una forma de combinar todo lo que ocurre en cualquiera de los dos conjuntos.
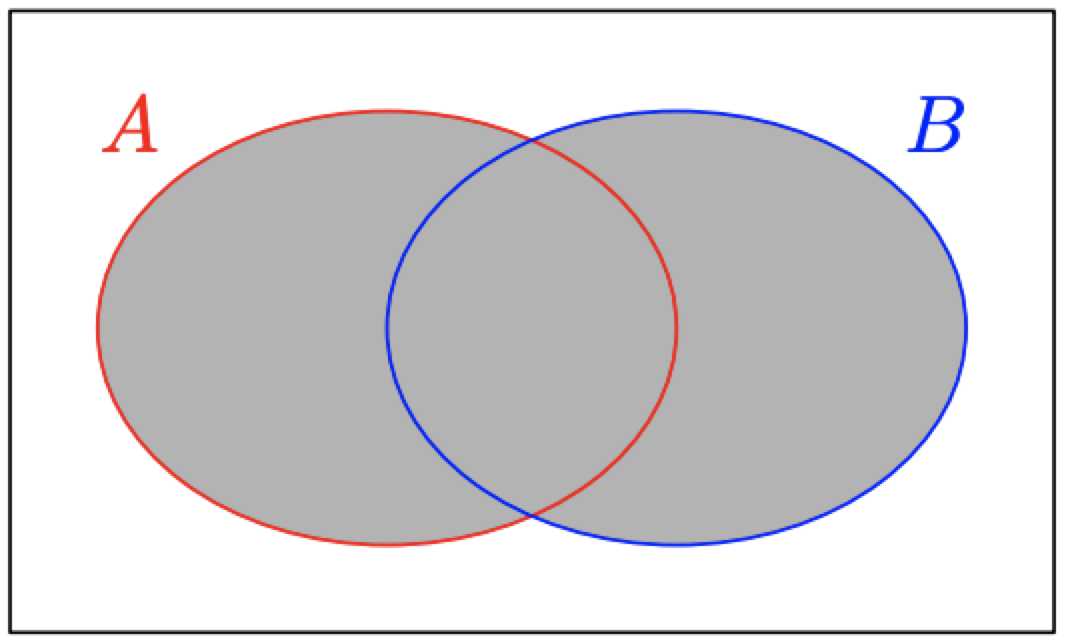
Esto lleva al siguiente consejo importante.
Nota
Cuando se le pida que encuentre la unión de dos conjuntos\(A\) y\(B,\) en su respuesta, incluya todo desde ambos conjuntos.
Desigualdades compuestas simples
Apliquemos lo que hemos aprendido para encontrar los sindicatos y/o intersecciones de intervalos de números reales. El enfoque más sencillo es a través de una serie de ejemplos. Empecemos.
Ejemplo\(\PageIndex{3}\)
En la línea real, esboza el conjunto de números reales en el conjunto\(\{x : x < 3\) o\(x < 5\}.\) Usa notación de intervalo para describir tu respuesta final.
Solución
Primero, hagamos un boceto de dos conjuntos,\(\{x : x < 3\}\) y\(\{x : x < 5\},\) en líneas reales separadas, una encima de la otra como se muestra en la Figura\(\PageIndex{8}\).
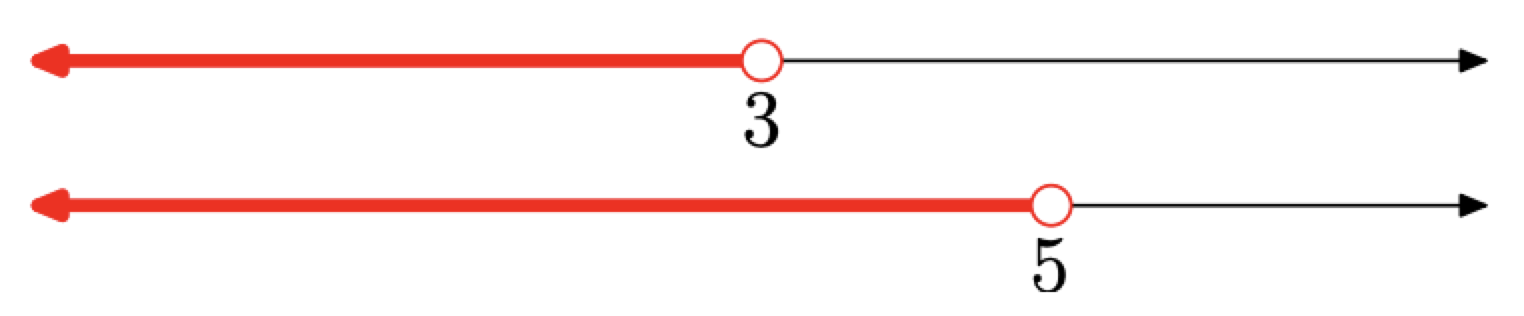
Ahora, para bosquejar la solución, anotar la palabra “\(\{x : x < 3\)o” en el conjunto o\(x < 5\}.\) Así, necesitamos tomar la unión de las dos líneas reales sombreadas en Figura\(\PageIndex{8}\). Es decir, necesitamos sombrear todo lo que esté sombreado en cualquiera de las dos líneas numéricos. Por supuesto, esto sería todo menos de 5, como se muestra en la Figura\(\PageIndex{9}\).

Así, la solución final es\(\{x : x < 5\},\) cual en notación de intervalos, es\((-\infty, 5)\).
Veamos otro ejemplo.
Ejemplo\(\PageIndex{4}\)
En la línea real, esboza el conjunto de números reales en el conjunto\(\{x : x < 3\) y\(x < 5\}.\) Usa la notación de intervalos para describir tu respuesta final.
Solución
En Ejemplo\(\PageIndex{3}\), se le pidió que sombreara el set\(\{x : x < 3\) o\(x < 5\}\) en la línea real. En este ejemplo, se nos pide que bosquejemos el conjunto\(\{x : x < 3\) y\(x < 5\}.\) Note que las notaciones set-builder son idénticas excepto por un cambio, la “o” de Ejemplo\(\PageIndex{3}\) ha sido reemplazada por la palabra “y”.
Nuevamente, dibuje dos conjuntos,\(\{x : x < 3\}\) y\(\{x : x < 5\},\) en líneas reales separadas, una encima de la otra como se muestra en la Figura\(\PageIndex{10}\).
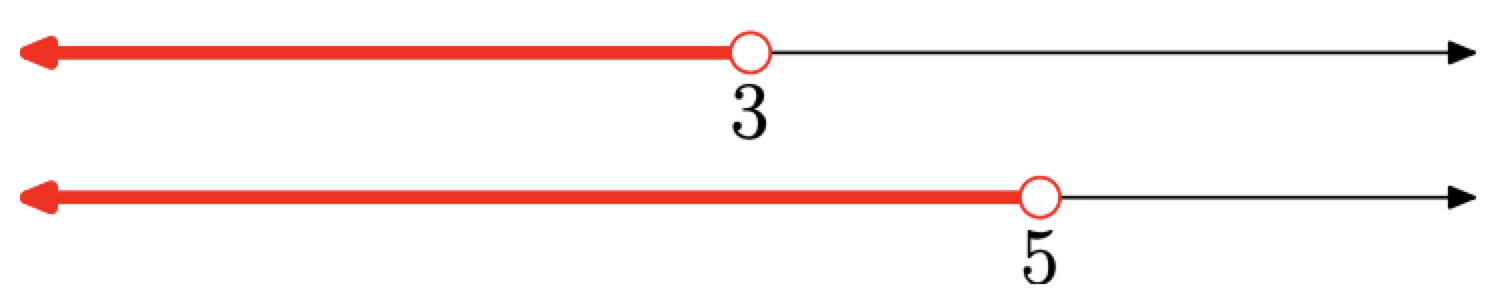
Ahora, para bosquejar la solución, anote la palabra “\(\{x : x < 3\)y” en el conjunto y\(x < 5\}.\) Así, necesitamos tomar la intersección de las dos líneas reales sombreadas en la Figura\(\PageIndex{10}\). Es decir, necesitamos sombrear todo lo que es común a las dos líneas numéricos. Por supuesto, esto sería todo menos de 3, como se muestra en la Figura\(\PageIndex{11}\).

Así, la solución final es\(\{x : x < 3\},\) cual en notación de intervalos, es\((-\infty, 3)\).
Nota
Si contestas “o” cuando la respuesta requiere “y”, o viceversa, no has cometido un error menor. En efecto, se trata de un enorme error, como se demuestra en Ejemplo\(\PageIndex{3}\) y Ejemplo\(\PageIndex{4}\).
Antes de intentar otro ejemplo, hacemos una pausa para definir un poco de notación que será sumamente importante en nuestro próximo trabajo.
Definición
La notación
\[a<x<b\]
se interpreta en el sentido de
\[x>a \text { and } x<b\]
Alternativamente, podríamos haber dicho que\(a < x < b\) es idéntico a decir “\(a < x\)y\(x < b,\)” pero decir “\(a < x\)” es lo mismo que decir “\(x > a.\)” Preferimos decir “\(x > a\)y\(x < b,\)” y usaremos este orden a lo largo de nuestro trabajo, pero la forma “\(a < x\)y\(x < b\)” es igualmente válido.
El punto realmente clave a hacer aquí es el hecho de que la declaración\(a < x < b\) es una declaración “y”. Si se usa correctamente, es una buena manera de describir los números que se encuentran entre\(a\) y\(b.\)
Veamos un ejemplo.
Ejemplo\(\PageIndex{5}\)
En la línea real, esboza el conjunto de números reales en el conjunto\(\{x : 3 < x < 5\}.\) Usa notación de intervalo para describir tu respuesta.
Solución
Primero, escribamos lo que significa la notación\(\{x : 3 < x < 5\}.\) Por definición, este conjunto es el mismo que el conjunto
\[\{x : x>3 \text { and } x<5\}\nonumber\]
Así, el primer paso es esbozar los conjuntos\(\{x : x > 3\}\) y\(\{x : x < 5\}\) sobre líneas reales individuales, apiladas una encima de la otra, como se muestra en la Figura\(\PageIndex{12}\).

Ahora, para bosquejar la solución, anotar la palabra “y” en el conjunto\(\{x : x > 3\) y\(x < 5\}.\) Así, necesitamos tomar la intersección de las dos líneas en la Figura\(\PageIndex{12}\). Es decir, necesitamos sombrear los números en la línea real que son comunes a las dos líneas que se muestran en la Figura\(\PageIndex{12}\). Los números 3 y 5 no están sombreados en ambos conjuntos de la Figura\(\PageIndex{12}\), por lo que no serán sombreados en nuestra solución final. Sin embargo, todos los números reales entre 3 y 5 están sombreados en ambos conjuntos en la Figura\(\PageIndex{12}\), por lo que estos números serán sombreados en la solución final mostrada en la Figura\(\PageIndex{13}\).

De una manera muy natural, la notación de intervalo para la solución sombreada en la Figura\(\PageIndex{13}\) es Es\((3, 5).\) decir,
\[(3,5)=\{x : 3<x<5\}\]
De igual manera, aquí están las notaciones set-builder e interval, así como el sombreado de los sets en la línea real, para varias situaciones, incluida la que acabamos de discutir.
| Línea numéricos | Notación Set-Builder | Notación de intervalos |
|---|---|---|
 |
\(\{x : 3 < x < 5\}\) | \((3,5)\) |
 |
\(\{x : 3 \leq x \leq 5\}\) |
\([3,5]\) |
 |
\(\{x : 3 \leq x < 5\}\) | \([3,5)\) |
 |
\(\{x : 3 < x \leq 5\}\) | \((3,5]\) |
Hay varios puntos de énfasis respecto a los intervalos en la Tabla\(\PageIndex{4}\).
- Cuando queremos enfatizar que no estamos incluyendo un punto en la línea real, usamos un “círculo vacío”. Por el contrario, un “círculo lleno” significa que estamos incluyendo el punto en la línea real. Así, el intervalo en la primera fila de Tabla\(\PageIndex{4}\) no incluye los puntos finales en 3 y 5, pero el intervalo en la segunda fila de Tabla\(\PageIndex{4}\) sí incluye los puntos finales en 3 y 5.
- El uso de un paréntesis en la notación de intervalo significa que no estamos incluyendo ese punto final en el intervalo. Así, los paréntesis utilizados\((3, 5)\) en la primera fila de Tabla\(\PageIndex{4}\) significan que no estamos incluyendo los números 3 y 5 en ese intervalo.
- El uso de un corchete en la notación de intervalo significa que estamos incluyendo el número entre corchetes en el intervalo. Así, los corchetes utilizados en\([3, 5],\) como se ve en la segunda fila de Tabla\(\PageIndex{4}\), significa que estamos incluyendo los números 3 y 5 en el intervalo.
- Por último, tenga en cuenta que algunos de nuestros intervalos son “abiertos” en un extremo pero “cerrados” (llenos) en el otro extremo, como los de las filas 3 y 4 de la Tabla\(\PageIndex{4}\).
Definición
Alguna terminología:
- El intervalo\((3, 5)\) está abierto en cada extremo. Por lo tanto, llamamos al intervalo\((3, 5)\) un intervalo abierto.
- El intervalo\([3, 5]\) se cierra (llena) en cada extremo. Por lo tanto, llamamos al intervalo\([3, 5]\) un intervalo cerrado.
- Los intervalos\((3, 5]\) y no\([3, 5)\) son ni abiertos ni cerrados.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{6}\)
En la línea real, bosquejar el conjunto de todos los números reales en el conjunto\(\{x : x > 3\) o\(x < 5\}\). Usa la notación de intervalos para describir tu respuesta.
Solución
Tenga en cuenta que la única diferencia entre este ejemplo actual y el conjunto sombreado en Ejemplo\(\PageIndex{4}\) es el hecho de que hemos reemplazado la palabra “y” en\(\{x : x > 3\) y\(x < 5\}\) por la palabra “o” en\(\{x : x > 3\) o\(x < 5\}\). Pero, como hemos visto antes, esto puede marcar una gran diferencia.
Así, el primer paso es esbozar los conjuntos\(\{x : x > 3\}\) y\(\{x : x < 5\}\) sobre líneas reales individuales, apiladas una encima de la otra, como se muestra en la Figura\(\PageIndex{14}\).

Ahora, para bosquejar la solución, anote la palabra “o” en el set\(\{x : x > 3 or x < 5\}\). Así, necesitamos tomar la unión de las dos líneas en la Figura\(\PageIndex{14}\). Es decir, necesitamos sombrear los números en la línea real que están sombreados en cualquiera de las dos líneas que se muestran en la Figura\(\PageIndex{14}\). No obstante, esto significa que tendremos que sombrear cada número de la línea, como se muestra en la Figura\(\PageIndex{15}\). Notarás que no hay etiquetas para 3 y 5 en la línea real de la Figura\(\PageIndex{15}\), ya que no hay puntos finales en esta solución. Los puntos finales, si se quiere, están en el infinito negativo y positivo.

Así, de una manera más natural, la notación de intervalo para la solución sombreada en la Figura\(\PageIndex{15}\) es\((-\infty, \infty)\).
Veamos otro ejemplo.
Ejemplo\(\PageIndex{7}\)
En la línea real, bosquejar el conjunto de todos los números reales en el conjunto\(\{x : x < −1\) o\(x > 3\}\). Usa la notación de intervalos para describir tu respuesta.
Solución
El primer paso es bosquejar los conjuntos\(\{x : x < −1\}\) y\(\{x : x > 3\}\) en líneas reales separadas, apiladas una encima de la otra, como se muestra en la Figura\(\PageIndex{16}\).

Para bosquejar la solución, anote la palabra “o” en el conjunto\(\{x : x < −1\) o\(x > 3\}\). Así, necesitamos tomar la unión de las dos líneas reales sombreadas en la Figura\(\PageIndex{16}\). Es decir, necesitamos sombrear los números en la línea real que están sombreados en cualquiera de las líneas reales de la Figura\(\PageIndex{16}\). Así, cada número menor que −1 está sombreado, así como cada número mayor que 3. El resultado se muestra en la Figura\(\PageIndex{17}\).

Aquí hay un consejo importante.
Nota
Si desea utilizar correctamente la notación de intervalos, siga una regla simple: Siempre barre los ojos de izquierda a derecha describiendo lo que ve sombreado en la línea real.
Si seguimos este consejo, al barrer los ojos de izquierda a derecha a través de la línea real sombreada en la Figura\(\PageIndex{17}\), vemos que los números están sombreados desde el infinito negativo hasta −1, y del 3 al infinito positivo. Así, de una manera más natural, la notación de intervalo para la solución sombreada establecida en la Figura\(\PageIndex{17}\) es
\[(-\infty,-1) \cup(3, \infty)\nonumber\]
Hay varios puntos importantes que hacer aquí:
Observe cómo usamos el símbolo de unión\(\cup\) para unir los dos intervalos de manera natural.\((-\infty,-1) \cup(3, \infty)\)
El símbolo de unión se usa entre conjuntos de números, mientras que la palabra “o” se usa entre declaraciones sobre números. Es incorrecto intercambiar los roles del símbolo de unión y la palabra “o”. Así, la escritura\(\{x : x<-1 \cup x>3\}\) es incorrecta, ya que también sería escribir\((-\infty,-1)\) o\((3, \infty)\).
Reforzamos la discusión anterior sobre la diferencia entre círculos, corchetes y paréntesis “llenos” y “abiertos” en la Tabla 5, donde incluimos varias comparaciones de notación de intervalo y set-builder, incluyendo la solución actual a Ejemplo\(\PageIndex{7}\).
| Línea numérica | Notación Set-Builder | Notación de intervalos |
|---|---|---|
 |
\(\{x : x<-1\)o\(x>3\}\) | \((-\infty,-1) \cup(3, \infty)\) |
 |
\(\{x : x \leq-1\)o\(x \geq 3\}\) | \((-\infty,-1] \cup[3, \infty)\) |
 |
\(\{x : x \leq-1\)o\(x>3\}\) | \((-\infty,-1] \cup(3, \infty)\) |
 |
\(\{x : x<-1\)o\(x \geq 3\}\) | \((-\infty,-1) \cup[3, \infty)\) |
Nuevamente, reforzamos los siguientes puntos.
- Observe cómo barrer los ojos de izquierda a derecha, al describir lo que está sombreado en la línea real, asegura que escriba la notación de intervalo en el orden correcto.
- Un corchete es equivalente a un punto relleno e incluye el punto final, mientras que un paréntesis es equivalente a un punto abierto y no incluye el punto final.
Hagamos un último ejemplo que debería cimentar para siempre la noción de que hay una enorme diferencia entre las palabras “y” y “o”.
Ejemplo\(\PageIndex{8}\)
En la línea real, bosquejar el conjunto de todos los números reales en el conjunto\(\{x : x<-1\) y\(x>3\}\). Describe tu solución.
Solución
En primer lugar, tenga en cuenta que la única diferencia entre este ejemplo y Ejemplo\(\PageIndex{6}\) es el hecho de que cambiamos el “o” en\(\{x : x<-1\) o\(x>3\}\) por un “y” en\(\{x : x<-1\) y\(x>3\}\). Los bocetos preliminares son idénticos a los de la Figura\(\PageIndex{16}\).

Ahora, anote la palabra “y” en\(\{x : x < −1\text{ and }x > 3\}\). Por lo tanto, necesitamos tomar la intersección de las líneas reales sombreadas en la Figura\(\PageIndex{18}\). Es decir, necesitamos sombrear en una sola línea real todos los números que están sombreados en ambas líneas reales en Figura\(\PageIndex{18}\). Sin embargo, no hay puntos sombreados en común en las líneas reales de la Figura\(\PageIndex{18}\), por lo que el conjunto de soluciones está vacío, como se muestra en la Figura\(\PageIndex{19}\).

¡Bastante impresionante! Los dos últimos ejemplos demuestran claramente que si intercambias los roles de “y” y “o”, no has cometido un error menor. En efecto, has cambiado todo el significado del problema. Entonces, ten cuidado con tus “ands” y “ors”.


